PPO 近端策略优化算法：ChatGPT默认的强化学习策略

PPO 近端策略优化算法

• • PPO = 演员-评论家算法 + 概率比率裁剪
  • • 演员-评论家
    • • 策略梯度算法
      • • 计算智能体策略预期奖励的梯度
        • • 公式分解
          • 时间流程拆解
        • 通过采样方法近似估计梯度
        • • 公式拆解
          • 时间流程拆解
        • 改进策略
        • • 引入基线
      • DQN算法
    • 概率比率裁剪

?

---

PPO = 演员-评论家算法 + 概率比率裁剪

PPO 直接优化了策略（即智能体的行为模式），而不是优化一个价值函数（如Q值）。

• 策略是训练对象，等同于机器。

PPO算法采用了演员-评论家的框架，但强调使用 概率比率裁剪 技巧来控制策略更新的幅度，以确保训练的稳定性和性能。

• 概率比率裁剪：在每次策略更新时，它计算新策略和旧策略之间的比率，并通过限制这个比率的大小来裁剪更新幅度，以防止过大的改变。这有助于保持训练的稳定性。

演员-评论家：策略梯度算法（演员） 和 DQN算法（评论家） 组合，能在连续场景下得到实时反馈。

• 如果不明白来龙去脉，看一下强化学习的介绍就明白了，请猛击：【OpenAI Q* 超越人类的自主系统】DQN ：Q-Learning + 深度神经网络

演员-评论家

演员-评论家（Actor-Critic）方法是一种强化学习算法，结合了基于概率分布的策略梯度算法（演员部分）和基于行为价值函数方法（评论家部分）。

1. 双组件结构：演员-评论家方法由两部分组成：

   • 演员（Actor）：负责选择行为。演员基于当前的策略来决定下一个执行的动作。
   • 评论家（Critic）：评估行为。评论家估计当前策略下采取某动作的好坏，通常通过计算值函数（如状态值函数或动作值函数）来实现。

2. 策略和值函数的结合：

   • 演员直接学习策略，而评论家估计价值函数。这种结合提供了策略梯度的优势（直接优化策略）和值函数优势（减少方差，加速学习）。
   • 如果用边想边干比喻，想就是求价值函数，干就是求策略函数。
   • 好的“想”（价值函数的准确估计）会导致更好的“干”（更有效的策略），而有效的“干”（实践中的行动）又会回过头来改进“想”的过程（更准确的价值估计）。

3. 策略更新：演员根据评论家提供的反馈来更新其策略。这通常通过策略梯度方法实现，其中梯度由评论家的估计值指导。

4. 减少方差：使用评论家可以减少策略梯度估计的方差，因为评论家提供了对预期奖励的更准确估计。

5. 持续学习：演员-评论家方法适用于持续的任务，其中智能体需要不断地做出决策并从经验中学习。

6. 探索和利用：如同其他强化学习算法，演员-评论家也需要在探索（尝试新的、可能更好的行为）和利用（使用已知的最佳行为）之间找到平衡。

演员-评论家算法分成两半，一半是演员，另一半是评论家。

• 演员：这一半基于概率分布，策略梯度算法。它有一个神经网络，可以根据行为的概率，选出行为。

• 评论家：这一半基于行为价值，DQN 算法。它有一个神经网络，可以根据行为的价值进行打分。

将概率分布和行为价值的方法相结合：

• 由基于概率分布的策略网络在连续场景中选出行为
• 由基于行为价值的价值网络给行为提供实时反馈

话分俩头，先说一下策略梯度算法，再说DQN算法。

策略梯度算法

策略梯度算法，用于优化策略。

• 在强化学习中，策略定义了一个智能体在给定状态下选择动作的方式

• 策略梯度算法的目的是通过调整策略参数来最大化累积奖励

• 核心思想是直接对策略进行参数化，并使用梯度上升（或下降）方法来更新策略参数

比如在走迷宫或打败敌人。

策略梯度算法就是一种方法，用来教会这个智能体如何做出最好的决策。

策略 指的是智能体在特定情况下应该做什么动作的规则。

例如，在看到敌人时，策略可能是攻击或逃跑。

策略梯度算法的目标是找到最优的策略，即让智能体在游戏中获得最高分数或奖励的策略。

工作方式是这样的：

1. 尝试和错误：智能体开始时可能不知道什么是最好的行动，所以它会尝试不同的动作来看哪些动作能得到更好的结果。

2. 评估和学习：每次智能体做出决策并看到结果后，策略梯度算法会评估这个决策是好是坏，并根据这个评估来调整智能体的策略。如果某个动作导致了好结果（比如赢得更多分数），算法就会倾向于让智能体未来更多地采取这个动作。

3. 梯度上升：这个调整过程类似于数学中的梯度上升方法。算法计算每个动作如何影响最终奖励的概率，并调整策略以增加获得更高奖励的动作的概率。

4. 持续改进：随着智能体不断尝试和学习，它的策略会逐渐改进，最终找到一种策略，使它能在游戏中获得最高的奖励。

这个公式是策略梯度算法中的核心数学表达，涉及到了如何更新一个智能体的策略来获得更好的表现。让我们逐步分解这个公式，以便于更容易理解。

计算智能体策略预期奖励的梯度

$\begin{array}{rl}{\bar{R}}_{\theta }& =\sum _{\tau }R(\tau )p_{\theta }(\tau )={\mathbb{E}}_{r～p_{\theta }(\tau )}[R(\tau )]\\ & \\ p_{\theta }\left({\tau }^n\right)& =\sum _{t=1}^{r_n}{p}_{\theta }\left(a_t^n\mid s_t^n\right)\\ & \\ \theta & \leftarrow \theta +\eta ?{\bar{R}}_{\theta }\end{array}$

公式分解

1. 第一行：$({\bar{R}}_{\theta }={\sum }_{\tau }R(\tau )p_{\theta }(\tau )={\mathbb{E}}_{r～p_{\theta }(\tau )}[R(\tau )])$

   • ${\bar{R}}_{\theta }$：这代表智能体在当前策略（由参数 $\theta$ 决定）下的预期奖励。
   • ${\sum }_{\tau }R(\tau )p_{\theta }(\tau )$：这个部分计算所有可能的行动序列 $(\tau )$的总奖励 $R(\tau )$，考虑到每个序列发生的概率 $p_{\theta }(\tau )$。
   • ${\mathbb{E}}_{r～p_{\theta }(\tau )}[R(\tau )]$：这是预期奖励的另一种表达方式，它是说，按照当前策略，我们预期能获得的平均奖励。

2. 第二行：$(p_{\theta }({\tau }^n)={\sum }_{t=1}^{r_n}{p}_{\theta }(a_t^n|s_t^n)$

   • $p_{\theta }({\tau }^n)$：这表示第 (n) 个行动序列 ${\tau }^n$ 发生的概率。
   • ${\sum }_{t=1}^{r_n}{p}_{\theta }(a_t^n|s_t^n)$：这个公式计算一个特定行动序列中每个动作发生的概率之和。换句话说，它把每个时间点的动作发生概率相乘，以得到整个序列的概率。

3. 第三行：$\theta \leftarrow \theta +\eta ?{\bar{R}}_{\theta }$

   • $\theta \leftarrow \theta +\eta ?{\bar{R}}_{\theta }$：这是参数更新的步骤。这里，$\theta$ 是策略参数，$\eta$ 是学习率（一种决定参数更新步长的值），$?{\bar{R}}_{\theta }$ 是预期奖励关于策略参数的梯度。

时间流程拆解

1. 开始状态：智能体有一组初始策略参数 $\theta$。

2. 行动和观察：智能体根据当前策略做出一系列行动，并观察到结果（奖励和新状态）。

3. 计算预期奖励：使用第一行的公式计算在当前策略下的预期奖励。

4. 计算概率：根据第二行的公式计算行动序列的概率。

5. 更新策略参数：使用第三行的更新规则来调整策略参数。梯度 $?{\bar{R}}_{\theta }$ 指向能提高预期奖励的方向，策略参数 $\theta$ 则沿着这个方向更新。

6. 重复过程：用新的策略参数 $\theta$ 重复上述过程，直到策略达到满意的效果或满足其他停止条件。

这个公式描述了智能体如何通过学习和经验逐渐改进其行为策略，目的是为了最大化其在给定任务中获得的总奖励。

通过不断地尝试、评估结果。
?

通过采样方法近似估计梯度

$\begin{array}{rl}& ?{\bar{R}}_{\theta }=\sum _{\tau }R(\tau )?p_{\theta }(\tau )\\ & =\sum _{\tau }R(\tau )p_{\theta }(\tau )\frac{?p_{\theta }(\tau )}{p_{\theta }(\tau )}\\ & =\sum _{\tau }R(\tau )p_{\theta }(\tau )?\log p_{\theta }(\tau )\\ & ={\mathbb{E}}_{\tau ～{\rho }_{\theta }(\tau )}\left[R(\tau )?\log p_{\theta }(\tau )\right]\\ & \approx \frac{1}{N}\sum _{n=1}^{N}R\left({\tau }^n\right)?\log p_{\theta }\left({\tau }^n\right)\\ & =\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R\left({\tau }^n\right)?\log p_{\theta }\left(a_t^n\mid s_t^n\right)\end{array}$

公式拆解

1. 第一行：$?{\bar{R}}_{\theta }={\sum }_{\tau }R(\tau )?p_{\theta }(\tau )$

   • 这里计算的是预期奖励 ${\bar{R}}_{\theta }$ 对策略参数 $\theta$ 的梯度。
   • ${\sum }_{\tau }$ 表示对所有可能的行动序列KaTeX parse error: Can't use function '\(' in math mode at position 1: \?(?\tau\)求和。
   • $R(\tau )$ 是一个特定行动序列的奖励。
   • $?p_{\theta }(\tau )$ 是该行动序列发生概率的梯度。

2. 第二行：利用概率的性质转换公式。

   • $\frac{?p_{\theta }(\tau )}{p_{\theta }(\tau )}$ 变成 $?\log p_{\theta }(\tau )$。这是因为梯度和对数的数学关系。

3. 第三行：${\mathbb{E}}_{\tau ～{\rho }_{\theta }(\tau )}[R(\tau )?\log p_{\theta }(\tau )]$

   • 这里转换成了预期值的形式，$\mathbb{E}$ 表示期望值，即按照当前策略 $\theta$ 下行动序列 $\tau$ 的分布 ${\rho }_{\theta }(\tau )$ 来计算。

4. 第四行：用采样的方法来近似计算这个期望值。

   • $\frac{1}{N}{\sum }_{n=1}^{N}R({\tau }^n)?\log p_{\theta }({\tau }^n)$ 是通过从策略 $\theta$ 中采样 (N) 个行动序列来近似这个期望值。

5. 第五行：进一步展开，考虑每个行动序列中的每个时间步。

   • ${\sum }_{t=1}^{T_n}R({\tau }^n)?\log p_{\theta }(a_t^n|s_t^n)$ 表示对每个行动序列中的每个动作 $(a_t^n)$ 和状态 $(s_t^n)$ 计算梯度的总和。

这个公式是策略梯度算法中用于计算策略梯度的一个详细公式。

它展示了如何通过梯度上升来更新策略参数 $\theta$，以便最大化总奖励 ${\bar{R}}_{\theta }$。我们可以按步骤拆解这个公式，以更容易理解的方式解释每个部分。

时间流程拆解

1. 开始：智能体在环境中执行动作，根据其策略 $(p_{\theta })$ 生成行动序列 $(\tau )$。

2. 收集数据：智能体收集一系列行动序列和相应的奖励 $(R(\tau ))$。

3. 计算梯度：对于每个采样的行动序列，计算 $(R({\tau }^n)?\log p_{\theta }({\tau }^n))$。这个步骤涉及到计算每个动作的概率的对数的梯度，并乘以相应的总奖励。

4. 平均梯度：对所有采样的行动序列计算的梯度求平均，得到对策略参数 $(\theta )$ 的平均更新方向。

5. 更新策略：最后，使用这个平均梯度来更新策略参数 $(\theta )$，以期望在未来的行动序列中获得更高的奖励。

改进策略

引入基线

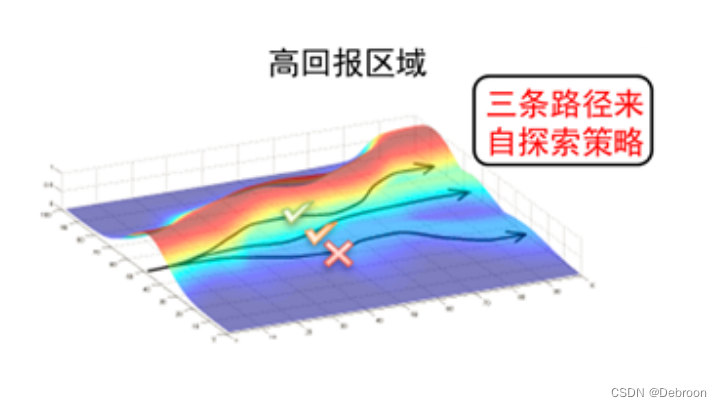
彩色的区域可能代表了不同的奖励值，

• 红色可能是高奖励区域
• 蓝色可能是低奖励区域

曲面上的箭头显示了优化过程中参数更新的路径，指向梯度的方向，即朝向奖励更高的区域。

• 不带基线的策略梯度：在没有基线的情况下，智能体可能会对每一步获得的奖励做出反应，不论这些奖励是高还是低。这可能导致智能体沿着曲面上的梯度盲目地寻找更高奖励的区域，这样的路径可能会很曲折，因为它会对每一个小波动都做出反应（打 X 的线）。

• 带基线的策略梯度：引入基线之后，智能体在更新其策略时，会考虑与基线的差异，而不仅仅是奖励的绝对值。这意味着，如果智能体在某个状态获得的奖励高于基线，它会认为这是一个好的行为，并倾向于未来重复这个行为；如果低于基线，则相反。这可以帮助智能体更平滑地沿着梯度上升的方向移动，避免了对奖励的小波动作出过度反应，最终可能找到一个更优化的路径。

在图中，如果我们将基线想象为一条穿过曲面的水平线，那么智能体的目标就是找到一个稳定的上升路径，而不是在每一个小坡度上都上下波动。

通过这种方式，基线就像是一个过滤器或稳定器，帮助智能体更有效地导航在奖励空间中，最终找到高奖励的顶峰。

$?{\bar{R}}_{\theta }\approx \frac{1}{N}{\sum }_{n=1}^N{\sum }_{t=1}^{T_n}\underset{\mathbf{Advantage}}{\underbrace{\left(R\left({\tau }^n\right)?b\right)}}??\log p_{\theta }\left(a_t^n\mid s_t^n\right)$

1. $?{\bar{R}}_{\theta }$：这表示我们要计算的目标，即策略的预期奖励 ${\bar{R}}_{\theta }$ 对策略参数 $\theta$ 的梯度。我们的目的是通过调整 $\theta$ 来最大化预期奖励。

2. $\frac{1}{N}{\sum }_{n=1}^N$：这表示取平均的操作。我们在许多不同的情况（称为情景或轨迹，表示为 ${\tau }^n$）下测试策略，并对结果取平均。这有助于我们得到一个更稳定、更普遍适用的策略更新。

3. ${\sum }_{t=1}^{T_n}$：这表示我们在每个轨迹中考虑每个时间步骤 (t)。对于每个时间步骤，智能体都会做出一个决策 $a_t^n$，并观察到结果 $s_t^n$。

4. $\left(R\left({\tau }^n\right)?b\right)$：这是“优势”（Advantage）部分，表示每个轨迹的总奖励 $R({\tau }^n)$ 减去一个基线 (b)。基线 (b) 通常是一个估计的平均奖励，这样优势就表示了在特定情况下获得的奖励比平均情况好多少。

5. $?\log p_{\theta }(a_t^n|s_t^n)$：这是策略梯度的核心部分。它表示智能体在时间步 (t)，给定状态 $s_t^n$，采取动作 $a_t^n$ 的策略的对数概率对参数 $\theta$ 的梯度。

流程顺序：

1. 生成轨迹：智能体在环境中按照当前策略 $\theta$ 行动，生成多个轨迹 ${\tau }^n$。

2. 计算每个轨迹的总奖励：对于每个轨迹，计算其获得的总奖励 $R({\tau }^n)$。

3. 计算优势：对每个轨迹，计算其优势，即总奖励减去基线 (b)。

4. 计算策略梯度：对于轨迹中的每个时间步骤，计算策略的对数概率关于参数 $\theta$ 的梯度。

5. 求和和平均：将所有轨迹的策略梯度加起来，然后除以轨迹的数量 (N)，得到平均梯度。

6. 更新策略参数：使用这个平均梯度来更新策略参数 $\theta$。

通过这个过程，策略梯度方法能够利用经验（即轨迹）来指导策略参数的更新，从而使智能体在环境中表现得更好。

DQN算法

请猛击：【OpenAI Q* 超越人类的自主系统】DQN ：Q-Learning + 深度神经网络

概率比率裁剪