MSCKF+OpenVins梳理
reference:
openvins学习中的问题https://zhuanlan.zhihu.com/p/355319559
OpenVins代码梳理https://www.zhihu.com/people/anson2004110/posts
OpenVINS能观一致性分析和FEJhttps://zhuanlan.zhihu.com/p/101478814
MSCKF那些事https://zhuanlan.zhihu.com/p/76894345
从MSCKF到OPENVINS https://zhuanlan.zhihu.com/p/56783450
官方文档中文翻译 https://blog.csdn.net/qq_39266065/article/details/128327291
整体框架
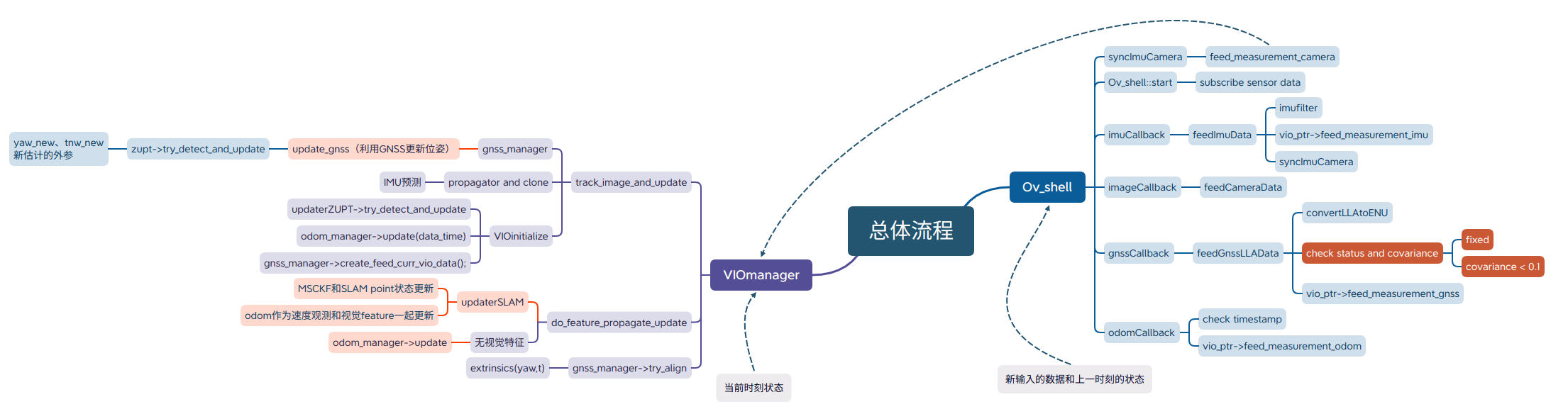
MSCKF
MSCKF核心思想
MSCKF的目标是解决EKF-SLAM的维数爆炸问题。传统EKF-SLAM将特征点加入到状态向量中与IMU状态一起估计,当环境很大时,特征点会非常多,状态向量维数会变得非常大。MSCKF不是将特征点加入到状态向量,而是将**不同时刻的相机位姿(位置 p和姿态四元数 q)**加入到状态向量,特征点会被多个相机看到,从而在多个相机状态(Multi-State)之间形成几何约束(Constraint),进而利用几何约束构建观测模型对EKF进行update。由于相机位姿的个数会远小于特征点的个数,MSCKF状态向量的维度相较EKF-SLAM大大降低,历史的相机状态会不断移除,只维持固定个数的的相机位姿(Sliding Window),从而对MSCKF后端的计算量进行限定。
IMU状态向量:
X I M U = [ q , b g , v , b a , p ] T X_{IMU}=[q,b_g,v,b_a,p]^T XIMU?=[q,bg?,v,ba?,p]T
其中
- q 为单位四元数,表示从世界系 ( G 系 ) 到 I M U 坐标系 ( I 系 ) 的 q为单位四元数,表示从世界系(G系)到IMU坐标系(I系)的 q为单位四元数,表示从世界系(G系)到IMU坐标系(I系)的旋转,长度为4
- b a 为加速度计 a c c e l e r a t o r 的偏差 b i a s b_a为加速度计accelerator的偏差bias ba?为加速度计accelerator的偏差bias
- G v 为 I M U 在 G 系下的 G_v为IMU在G系下的 Gv?为IMU在G系下的速度
- b g 为陀螺仪 g y r o s c o p e 的偏差 b i a s b_g为陀螺仪gyroscope的偏差bias bg?为陀螺仪gyroscope的偏差bias
- p I 为 I M U 在 G 系下的 p_I为IMU在G系下的 pI?为IMU在G系下的位置
四元数q的维度为4,转化为李代数后的维度为3,所以状态向量 X I M U X_{IMU} XIMU?的长度为16,而误差向量的长度为15。
将上述状态向量转化为李代数是为了方便优化求导和迭代。MSCKF的完整误差向量维度为15+6N
MSCKF状态向量:
X M S C K F = [ X I M U , p c 1 , q c 1 , p c 2 , p c 2 , … , p c N , q c N ] X_{MSCKF}=[X_{IMU},p_{c_1},q_{c_1},p_{c_2},p_{c_2},…,p_{c_N},q_{c_N}] XMSCKF?=[XIMU?,pc1??,qc1??,pc2??,pc2??,…,pcN??,qcN??]
观测模型
视觉中,约束通常都是特征点到相机的重投影误差(空间中一个3D特征点根据相机的姿态和位置投影到相机平面,与实际观测的特征点之间的误差)
我们希望用这个重投影误差的约束等式来作为观测模型,但前提是需要知道特征点的3D坐标,而实际应用中特征点的3D坐标是未知的。
MSCKF的做法是根据历史相机位姿和观测来三角化计算特征点的3D坐标。这又带来了一个问题:如何确保三角化的精度呢?如果三角化误差太大,那么观测模型就会不准,最终会使得VIO精度太差。MSCKF做法是当特征点跟踪丢失后再进行三角化,特征点跟丢表示该特征的观测不会再继续增加了,这时利用所有的历史观测三角化。所以MSCKF中观测更新的时机是特征点跟丢。
算法流程
- IMU积分:先利用IMU加速度和角速度对状态向量中的IMU状态进行预测,一般会处理多帧IMU观测数据。
- 相机状态扩增:每来一张图片后,计算当前相机状态并加入到状态向量中, 同时扩充状态协方差.
- 特征点三角化:然后根据历史相机状态三角化估计3D特征点
- 特征更新:再利用特征点对多个历史相机状态的约束,来更新状态向量。注意:这里不只修正历史相机状态,因为历史相机状态和IMU状态直接也存在关系(相机与IMU的外参),所以也会同时修正IMU状态。
- 历史相机状态移除:如果相机状态个数超过N,则剔除最老或最近的相机状态以及对应的协方差.
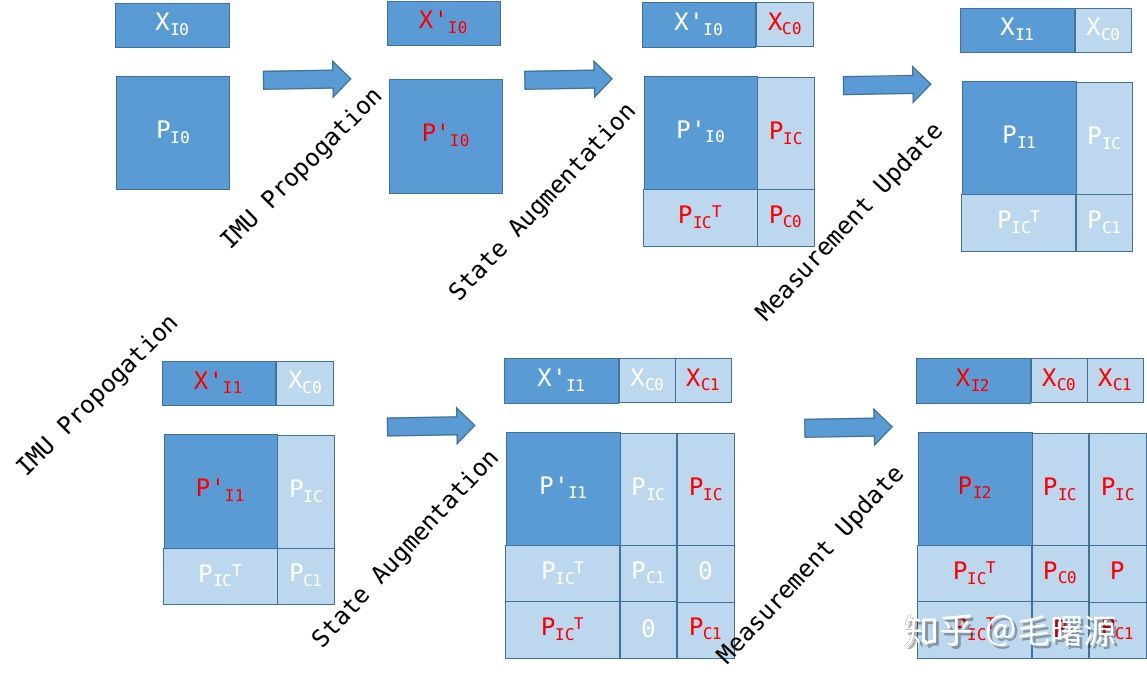
图中 X X X表示状态向量, P P P表示对应的协方差矩阵,红色部分为当前步骤改变的量。
OPENVINS
OpenVINS维护的协方差中包括15维的Q,P,V,Ba,Bg,1维的IMU和相机间的时间差dt,6维的左相机的位姿LCP,8维的左相机的LC相机内参,6维的右相机的位姿RCP,8维的右相机的RC相机内参,共计44维。

每一次位姿增广后(augment_clone),当前IMU位姿作为相机位姿(6维)加入到协方差中。例如在原程序中滑动窗口的长度为11,那么增广一个后就变成12,总维度为72。当滑窗个数超过11时会处理掉一帧IMU位姿(marginalize_old_clone),则又会变回11,总维度为66。另外,长期维护的特征点上限为50个(一个点x,y,z是三维),总计150维。
OpenVins流程:
- state propagator
- state initialize
- MSCKF updater
- SLAM updater
- zero velocity updates
IMU Propagation
利用两帧图像之间的所有IMU观测数据(加速度 a m a_m am?和角速度 w m w_m wm?),对MSCKF的状态向量和协方差进行迭代预测。它相当于EKF中的预测过程。
Propagator::predict_and_compute
预测IMU积分值,根据IMU积分更新状态量雅可比矩阵F和噪声雅可比矩阵Qd
状态向量预测(IMU积分)
- predict_mean_rk4()https://docs.openvins.com/propagation_analytical.html 根据IMU内参进行4阶Runge-Kutta积分,常用的三种数值积分:Euler积分、Mid-Point积分、Runge-Kutta积分(4阶)。它们的精度依次从低到高、计算量依次从小到大。令 k 2 k_2 k2?的权重为1,其他为0,RK4就退化为Mid-Point法;令 k 1 k_1 k1?的权重为1,其他为0,RK4就退化为Euler积分。
- predict_mean_discrete()https://docs.openvins.com/propagation_discrete.html根据离散的平均量进行积分
更新误差状态系数矩阵
构建离散噪声协方差矩阵
First-Estimate-Jacobian滑窗问题的解决(FEJ)
滑动窗口中的问题
滑动窗口算法中,对于同一个变量,不同残差对其计算雅克比矩阵时线性化点可能不一致,导致信息矩阵可以分成两部分,相当于在信息矩阵中多加了一些信息,使得其零空间出现了变化
解决办法: First Estimated Jacobian
FEJ 算法:不同残差对同一个状态求雅克比时,线性化点必须一致。这样就能避免零空间退化而使得不可观变量变得可观。
将计算出来的IMU状态量送进FEJ
state->_imu->set_fej(imu_x);
EKF Propagation
augment_clone
marginalize_slam
propagation time 0.0018s 0.0016s 0.0015s
feats_lost, feats_marg, feats_slam三步筛选:
- 如果lost点在别的相机可以观测到则保留,否则剔除掉
- 剔除lost中存在于feats_marg的点
- 如果跟踪到的点feats_marg数量达到max length 将超出的点设置为SLAM features候选
Append a new SLAM feature
如果数量没超过max 则将slamfeature候选全部加入设置为SLAM feature
遍历SLAM feature 确定marg点
对当前状态量marginalize_slam,将没有在当前帧中追踪到的边缘化掉
将SLAM feature分为update和delayed
将所有feature加入MSCKF,并根据track length进行排序
将最老的观测feature删掉
将协方差矩阵中对应的特征x_m删掉
// Generic covariance has this form for x_1, x_m, x_2. If we want to remove x_m:
//
// P_(x_1,x_1) P(x_1,x_m) P(x_1,x_2)
// P_(x_m,x_1) P(x_m,x_m) P(x_m,x_2)
// P_(x_2,x_1) P(x_2,x_m) P(x_2,x_2)
//
// to
//
// P_(x_1,x_1) P(x_1,x_2)
// P_(x_2,x_1) P(x_2,x_2)
//
// i.e. x_1 goes from 0 to marg_id, x_2 goes from marg_id+marg_size to Cov.rows() in the original covariance
更新MSCKF updaterMSCKF->update(state, featsup_MSCKF);

msckf time 0.021299s 0.012962s 0.007s
更新SLAMupdaterSLAM->update(state, featsup_TEMP);
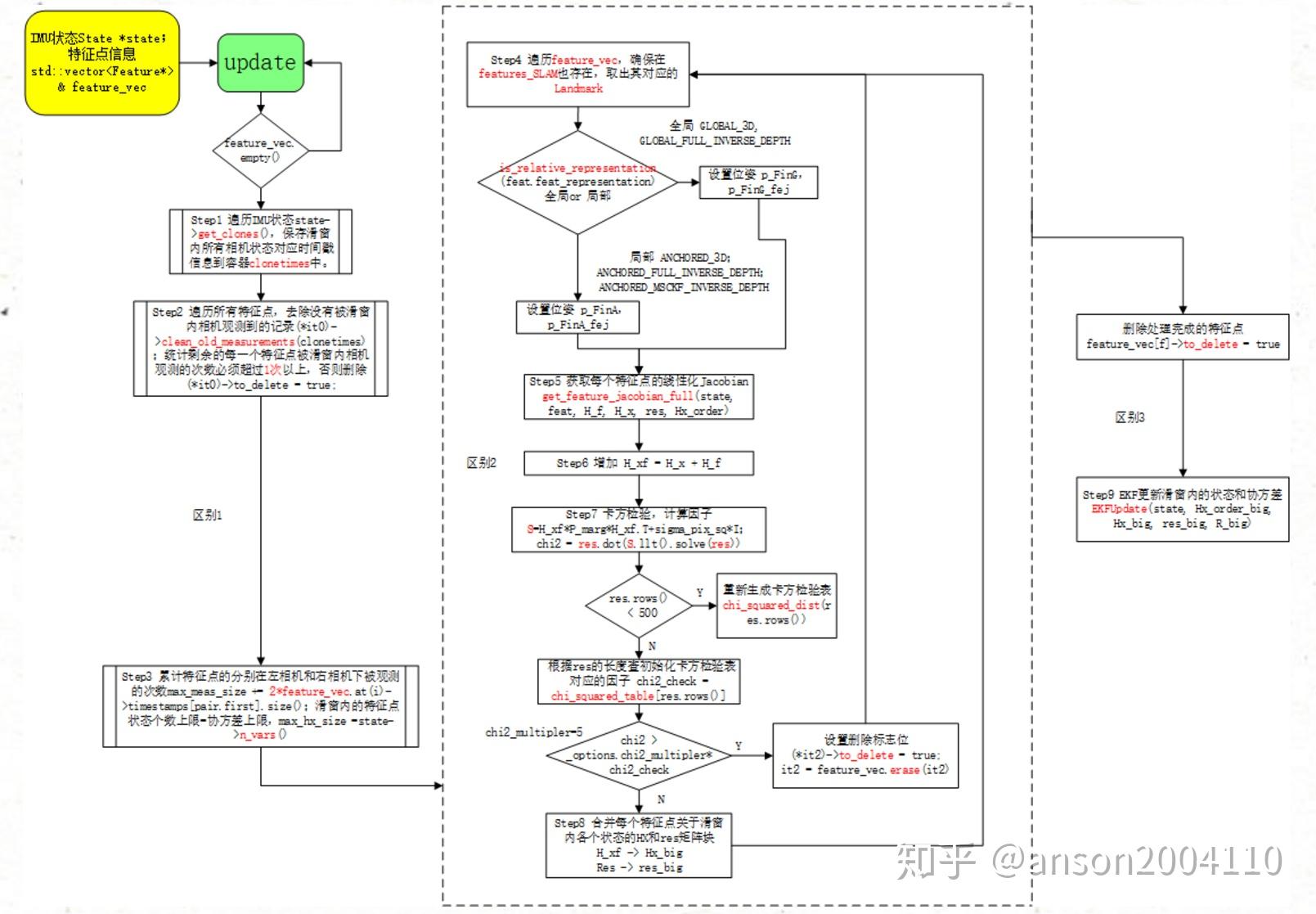
SLAM time 0.032213s 0.013258s 0.0035106s
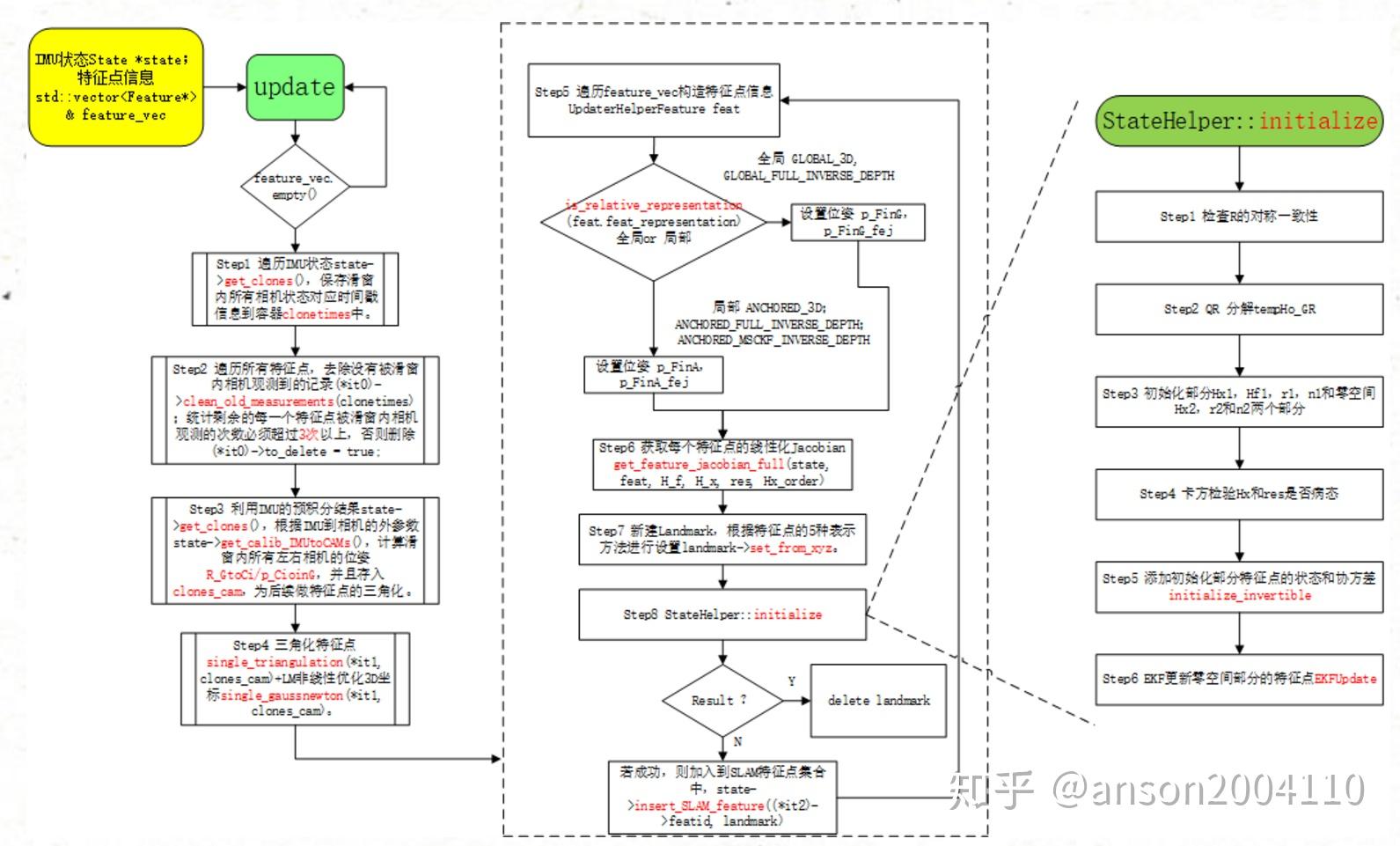
**delay_init time ** 0.014931s 0.0149179s 0.007424s
retriangulate_active_tracks
// Finally marginalize the oldest clone if needed
StateHelper::marginalize_old_clone(state);
re&marg time 0.022846s 0.021955s 0.02066s
根据相机观测计算雅可比矩阵
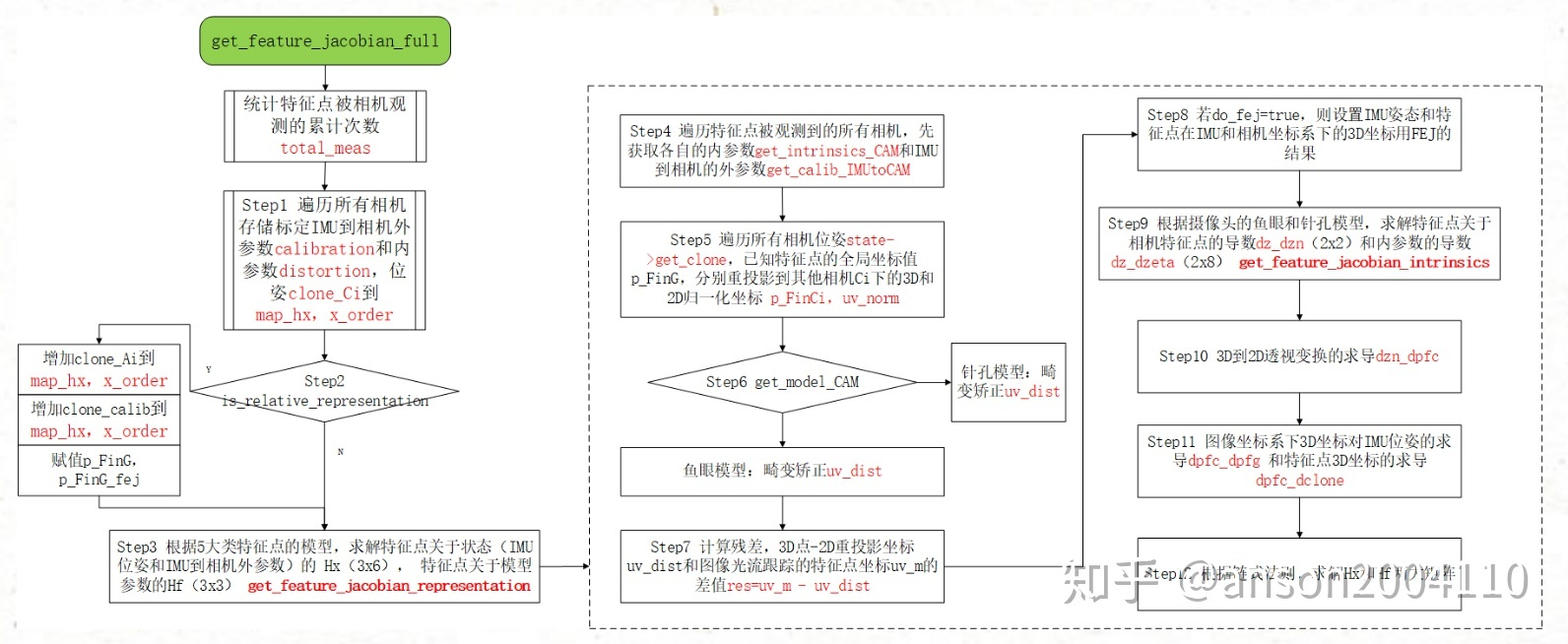
re&marg
retriangulate_active_tracks(message)
添加SLAM feature后重新对所有feature进行三角化和状态更新
- 对当前帧除了slam pts进行三角化,将3D点加入到active_tracks_posinG
- 对SLAMfeature 遍历进行三角化加入到active_tracks_posinG
- 将active_tracks_posinG中的3D点投影到当前帧中,保存uvd
对slam pts进行三角化
updaterSLAM->change_anchors(state);
StateHelper::marginalize_old_clone(state);
p_FinG feature in ground axis
- 取出当前帧的观测添加到每一个相机中,记录在cam0中的uv位置,跳过SLAM点
- 根据相机内参去畸变获得归一化平面坐标,将向量转化为反对称矩阵后添加到线性空间中。
- SVD分解求三角化
- 处理SLAM feature,将SLAMfeature投影到当前帧中
向量的零空间:
线性方程组Ax=0的所有解x的集合
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!