回溯法:概念以及解决迷宫老鼠问题
从一个问题开始
给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
很容易想到 用两个for循环就可以解决。
如果n为100,k为50呢,那就50层for循环,是不是开始窒息。
此时就会发现虽然想暴力搜索,但是用for循环嵌套连暴力都写不出来!
回溯法的概念
概念
通常以深度优先的方式系统地搜索问题的解的算法。
类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择, 尝试别的路径。
? “走不通就退回再走”
满足回溯条件的某个状态的点称为“回溯点”
回溯法的基本做法
是搜索,或是一种组织得井井有条的,能避免不必要搜索的穷举式搜索法。
使用场合
对于许多问题,当需要找出它的解的集合或者要求回答什么解是满足某些约束条件的最佳解时,往往要使用回溯法。
这种方法适用于解一些组合数相当大的问题,具有“通用解题法”之称。
基本思想
算法基本过程
将待求解问题看做一个解空间树, 问题的解可以表示为, 然后利用深度优先搜索逐步确定每一个解
,当搜索到树的叶子结点时, 就得到问题的一个解
.
当然这个解不一定是最优解,在将整个解空间树搜索完之后,通比较得到的每个,便可以得到最优解.
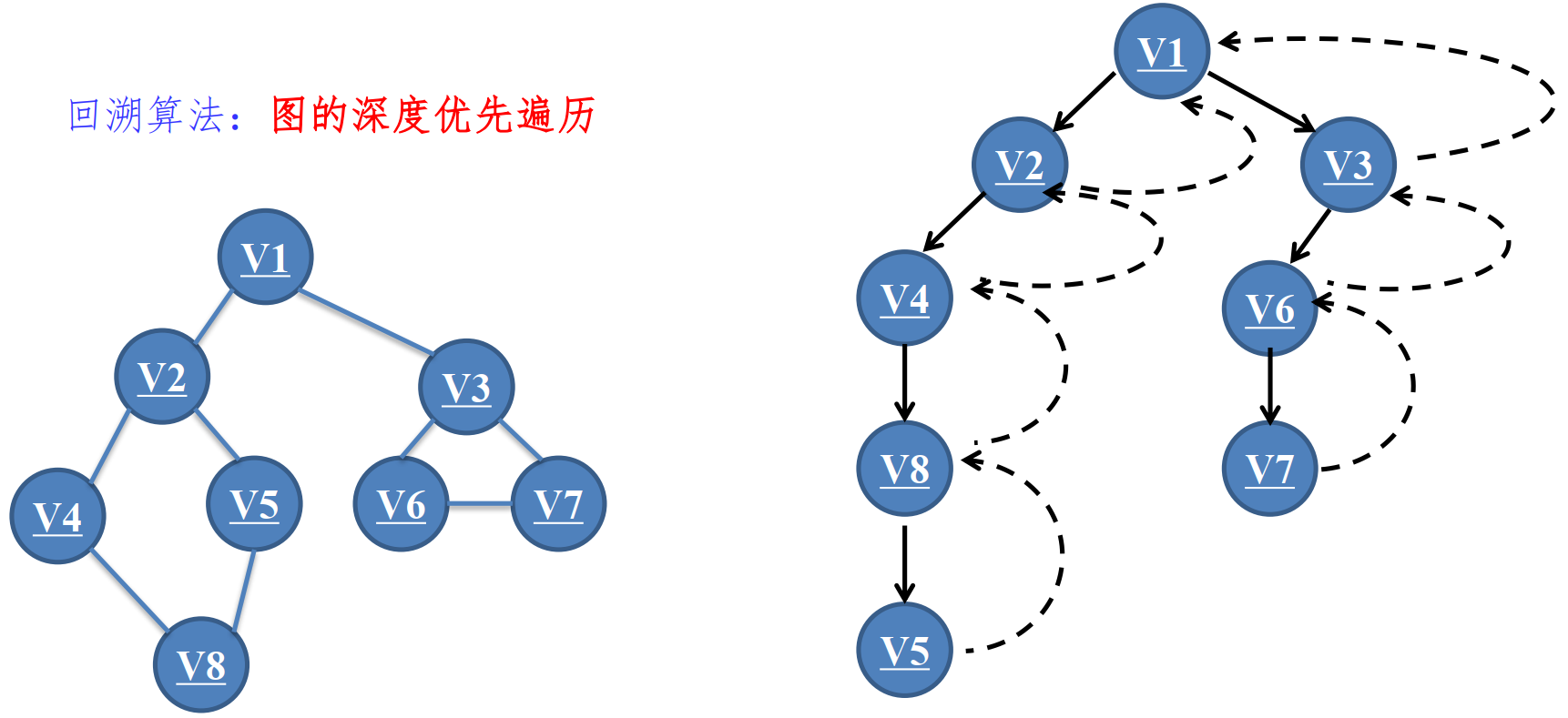
在搜索的过程中, 问题的解X需要满足约束条件P(X)。 在搜索到一个结点的时候发现当前结点不满足约束条件,则放弃向下搜索,即不再搜索该结点的子结点, 而是回溯到上一个结点继续搜索.
回溯法模版
参考文章:代码随想录
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
应用场景:迷宫老鼠问题
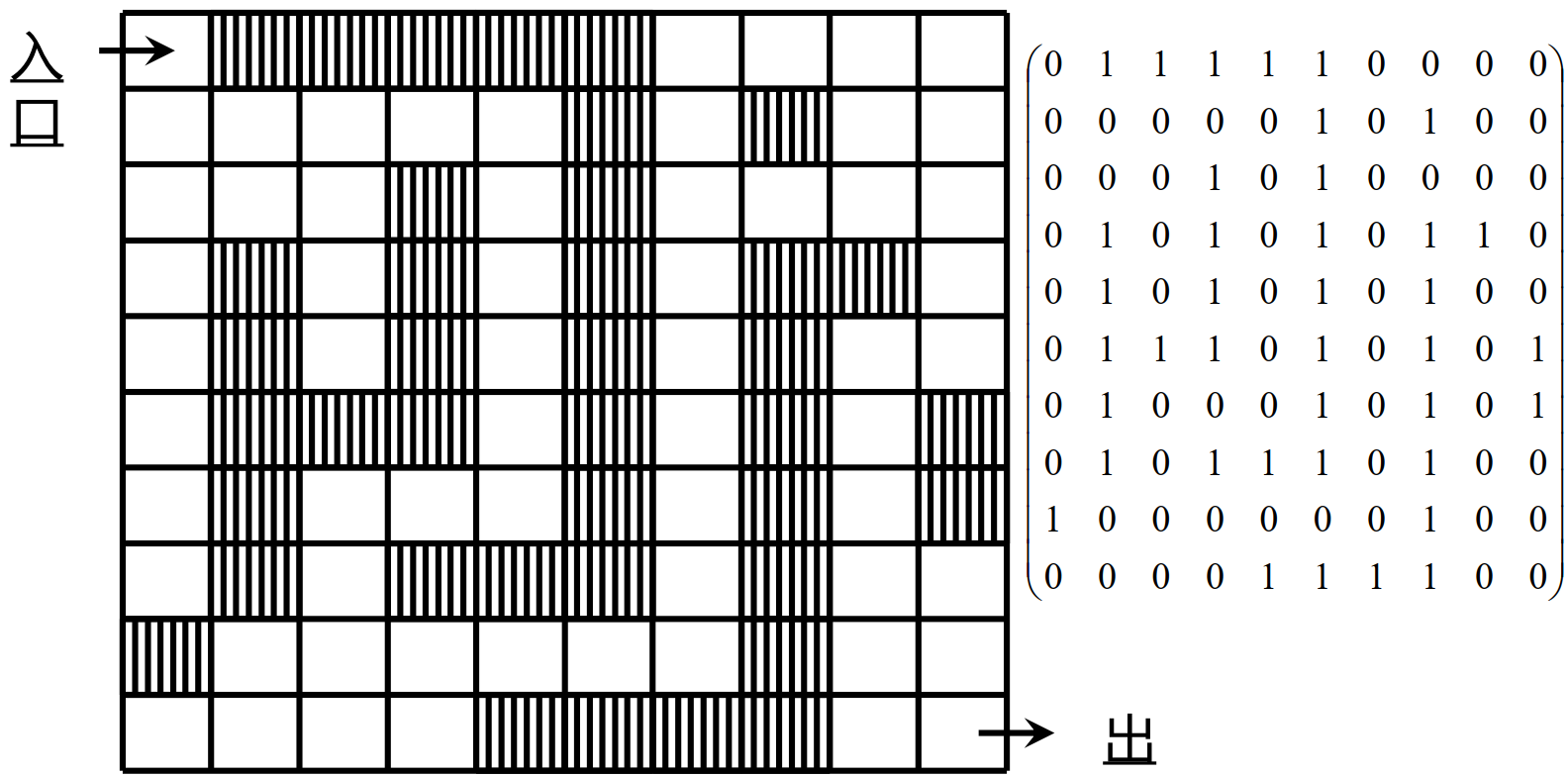
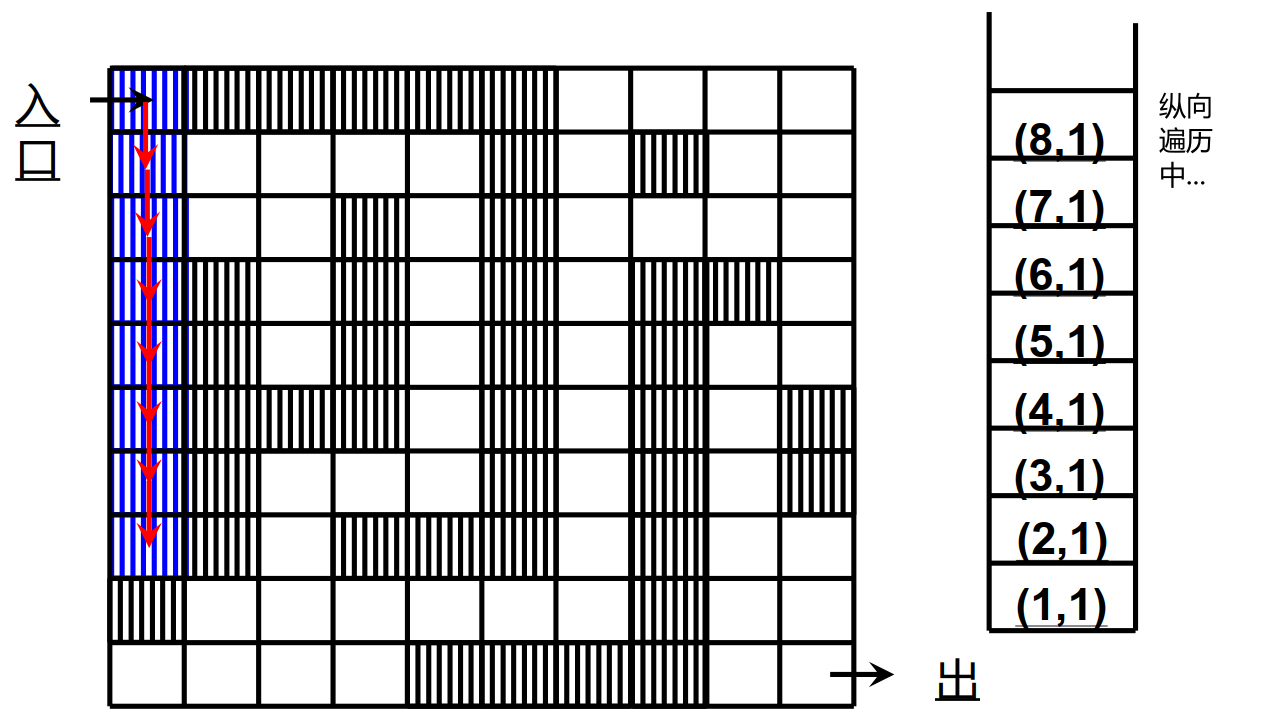
通过回溯法模版解决该问题
参考文章:java实现老鼠出迷宫_java迷宫鼠原理-CSDN博客
终止条件?
if (arr[x - 2][y - 2] == 2) {
return true; //设置通关路口为右下角(角口),注意这里arr[x - 1][y - 1]为墙壁
}回溯法的搜索过程?
// 处理节点
//先用2来表示走过的路径
arr[m][n] = 2;
//定义行走的路径顺序(下>右>上>左),采用回溯递归思想。走不通就回头
if (findway(arr, m + 1, n, x, y)) {
return true;
} else if (findway(arr, m, n + 1, x, y)) {
return true;
} else if (findway(arr, m - 1, n, x, y)) {
return true;
} else if (findway(arr, m, n - 1, x, y)) {
return true;
} else {
// 回溯,撤销处理的节点
//发现不管怎么走也走不了,故把刚刚改2的路径改为3表示死路
arr[m][n] = 3;
return false;
}回溯法解决迷宫老鼠问题?
package PAT;
import java.util.Scanner;
public class Test {
public static void main(String[] args) {
//构建地图
AA size = new AA();
Scanner print = new Scanner(System.in);
System.out.println("请输入地图的长和宽(给出大于6的值)");
int length = print.nextInt();
int wide = print.nextInt();
//调用函数制作地图并将结果传递给main中数组
int arr[][] = size.map(wide, length);
//遍历二维数组
System.out.println("地图如下:");
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr[i].length; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println(); //每输出一层换行
}
System.out.println();
BB find = new BB();
System.out.println("地图边界都是墙,并且下标从0开始");
System.out.println("请输入老鼠的起始位置(横坐标>=1)以及(列坐标):");
int start1 = print.nextInt();
int start2 = print.nextInt();
find.findway(arr, start1, start2, wide, length);
System.out.println("通关路径如下:");
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr[i].length; j++) {
System.out.print(arr[i][j] + " ");
}
//每输出一层换行
System.out.println();
}
}
}
class AA { //地图表示方法(1代表障碍 0代表空路 2代表路径 3代表死路)
public int[][] map(int n1, int n2) {
int arr[][] = new int[n1][n2]; //定义二维数组大小
//第一行和最后一行为置为1
for (int i = 0; i < n2; i++) {
arr[0][i] = 1;
arr[n1 - 1][i] = 1; //这里要减1目的是与下标一致
}
//第一列和最后一列为置为1
for (int i = 0; i < n1; i++) {
arr[i][0] = 1;
arr[i][n2 - 1] = 1;
}
//设置路障
arr[3][1] = 1;
arr[3][4] = 1;
arr[5][2] = 1;
return arr; //返回arr数组给main方法
}
}
class BB { //寻找路径方法
public boolean findway(int arr[][], int m, int n, int x, int y) { //定义m,n为起始位置
if (arr[x - 2][y - 2] == 2) {
return true; //设置通关路口为右下角(角口)
}
if (arr[m][n] == 0) { //当这个位置为0时代表可以走
// 处理节点
//先用2来表示走过的路径
arr[m][n] = 2;
//定义行走的路径顺序(下>右>上>左),采用回溯递归思想。走不通就回头
if (findway(arr, m + 1, n, x, y)) {
return true;
} else if (findway(arr, m, n + 1, x, y)) {
return true;
} else if (findway(arr, m - 1, n, x, y)) {
return true;
} else if (findway(arr, m, n - 1, x, y)) {
return true;
} else {
// 回溯,撤销处理的节点
//发现不管怎么走也走不了,故把刚刚改2的路径改为3表示死路
arr[m][n] = 3;
return false;
}
} else {
// 告诉上层没有通路
return false;
}
}
}回溯法与穷举查找是一样的吗?
相同点:
可以把回溯和分支限界看成是穷举法的一个改进。该方法至少可以对某些组合难题的较大实例求解。
不同点:
每次只构造侯选解的一个部分
然后评估这个部分构造解:如果加上剩余的分量也不可能求得一个解, 就绝对不会生成剩下的分量
参考文章
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Java动态代理
- Halcon图像增强equ_histo _image/emphasize/scale _image max/shock_filter
- Linux基础命令@grep、wc、管道符
- 30天精通Nodejs--第二十二天:express-认证和授权
- java数据结构与算法刷题-----LeetCode59. 螺旋矩阵 II
- 根据经纬度在百度地图使用logo标记位置,可点击logo查看详细信息
- Python导入模块,Python import用法(超级详细)
- 中通快递查询,中通快递单号查询,分析筛选出多次揽收件
- 输入部分实现
- 生物批签发数据库<收载15W+条数据>