常用的排序算法（二）

四、归并排序（Merge Sort）

归并排序的时间复杂度为O(nlogn)，在使用递归程序时，其额外空间复杂度为O(nlogn)

归并排序使用了一种叫做分而治之（Divide and conquer）的策略，将原本很庞大的数组排序问题分割成更小的子问题，在每一个子问题得到解决后，再合并它们。下面我们以数组arr[8]={9，2，4，6，3，0，8，7}为例，研究归并排序的解决思路：

我们首先将数组对半分开。分成两个大小为4的数组：

9

2

4

6

3

0

8

7

然后将大小为4的数组分开，分成大小为2的数组：

9

2

4

6

3

0

8

7

最后分成大小为1的数组，这样，每一个数组都保持有序（单一数据必有序）

9

2

4

6

3

0

8

7

接下来，我们要处理的便是将两个有序的子数组合并为一个有序数组的问题：

我们另外取一个例子，将arr1[4]={2,5,6,8}和arr2[4]={1,3,7,9}合并为大小为8的有序数组：

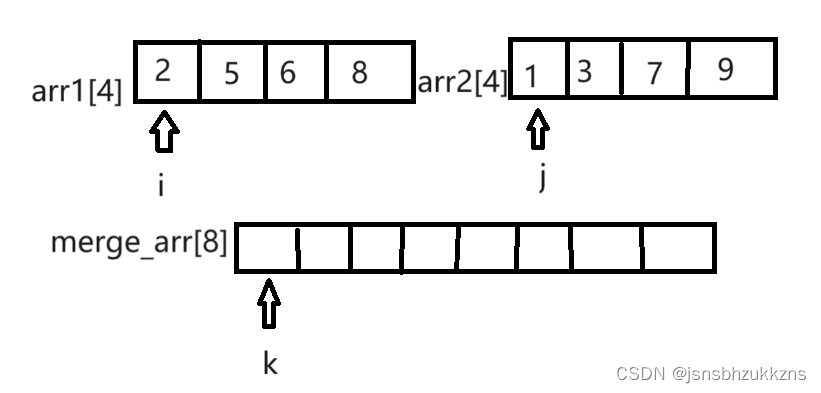
我们新开一个数组，大小为两个数组大小的和。维护3个指针i，j，k，分别指向arr1，arr2和新开数组的首地址。因为两个数组有序，所以所有数字的最小值一定在arr1[i]和arr2[j]中取到。我们只需比较arr1[i]和arr2[j]的大小，若arr1[i]较小，则将arr1[i]的值赋值给merge_arr[k]，随后i右移，k右移即可。当然，arr2[j]较大的情况也是同理。

当其中一个数组遍历完后，另外一个数组还没有被遍历完，只需要把没有遍历完的数组剩余的元素平移至merge_arr中的剩余空位中即可。

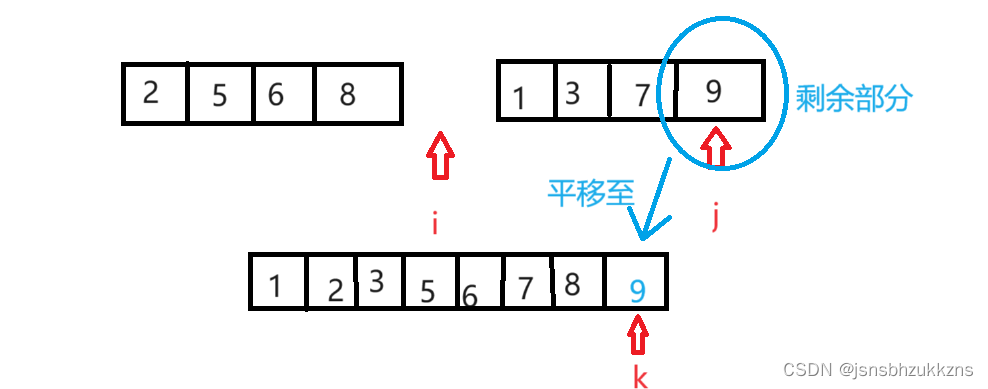
用上面的方法，我们就可以将两个有序的数组合并成一个有序的数组。

归并排序，就是拆分-合并的思路。

代码实现：

#include<stdio.h>
void Merge(int* arr,int start,int mid,int end){//合并两个有序数组
    if(start>=end){
        return;
    }
    int i=start;int j=mid+1;
    int k=0;//维护3个指针
    int size=end-start+1;
    int tmp[size];//新开一个数组，用来存放归并后的元素
    while(i<=mid&&j<=end){
        if(arr[i]<=arr[j]){
            tmp[k]=arr[i];
            i++;
            k++;
        }
        else{
            tmp[k]=arr[j];
            j++;
            k++;
        }
    }
    if(i==mid+1){
        while(j<=end){
            tmp[k]=arr[j];
            k++;
            j++;
        }
    }
    else if(j==end+1){
        while(i<=mid){
            tmp[k]=arr[i];
            i++;
            k++;
        }
    }//平移剩余元素
    k=0;
    i=start;
    while(i<=end){
        arr[i++]=tmp[k++];
    }//将归并后的元素一一赋值回原数组中
}
void Merge_Sort(int * arr,int start,int end){
    if(start>=end)return;
    int mid=(start+end)/2;//二分策略
    Merge_Sort(arr, start, mid);
    Merge_Sort(arr,mid+1,end);//左右两个数组依次归并
    Merge(arr,start,mid,end);//合并两个有序数组
}
int main(){
    int numsSize;
    scanf("%d",&numsSize);
    if(numsSize<=0){
        return 0x7fffffff;
    }//非法输入，直接返回
    int arr[numsSize];
    for(int i=0;i<numsSize;i++){
        scanf("%d",&arr[i]);
    }
    Merge_Sort(arr,0,numsSize-1);
    for(int i=0;i<numsSize;i++){
        printf("%d ",arr[i]);
    }
    return 0;
}

在归并排序的逻辑下，每一次问题的规模都会减半。于是递归的深度为O(logn),同一深度的递归所处理的元素个数之和为O(n)（因为数组的大小是固定的，你只是把它拆成一块一块的，或者两半，或者四部分，等等，但是加起来还是那么多数。这里停下来好好想一想），总的时间复杂度为O(nlogn)。

每个递归函数都要占用它排序的两个子数组的空间之和（因为它要开一个新的数组）。在递归结束之前，所有未执行完的函数所占用的额外空间都不会被释放。所以额外的空间复杂度为O(nlogn)。

其实，用循环代替递归是实现归并排序的一个好办法，它可以将空间复杂度降到O(n)，这个知识点不再涉及。（我不会）

五、快速排序（Quick Sort）

快速排序的平均时间复杂度为O(nlogn),最坏时间复杂度为O(n^2),递归程序中每次执行都要花费常数时间复杂度（用于交换元素），空间复杂度O(logn).

快速排序可以借助C语言的内置函数qsort()来实现,需要包含 stdlib.h 头文件。

qsort函数原型为：qsort(void* _Base,size_t_NumofElement,Size_OfElements, int (*_PtFuncCompare)(const void*,const void*))

一共有4个参数，第一个为要排序的数组，第二个为数组中待排元素的个数，第三个是数组中元素所占的字节数，第四个是表示排序原则的函数（递增还是递减）。

代码实现：

#include<stdio.h>
#include<stdlib.h>
int cmp(const void *a,const void *b){
    return *(int*)a-*(int*)b;
}
int main(){
    int numsSize;
    scanf("%d",&numsSize);
    int arr[numsSize];
    for(int i=0;i<numsSize;i++){
        scanf("%d",&arr[i]);
    }
    qsort(arr,numsSize,sizeof(int),cmp);
    for(int i=0;i<numsSize;i++){
        printf("%d ",arr[i]);
    }
}

?当然，仅仅掌握快速排序的代码实现是不够的。快速排序也借助了分而治之的思想，但快速排序是借助数组中的一个“主元”将数组中的元素拆分成为两部分：一部分比它小，另一部分比它大。然后对两部分再次进行上述操作。

我们借助int arr[11]={7, 13，4，6，5，2，11，15，0，3，8}研究快速排序的逻辑原理：

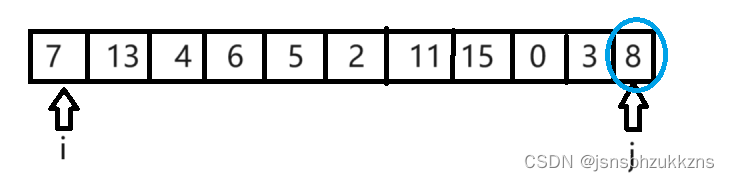
我们默认选取最后一个元素为主元，维护双指针i,j，分别指向arr[0]和arr[10]（除去主元之外最后的元素），将i后移动找到第一个比主元大的数13，然后固定i，向前移动j找到第一个比主元小的元素3，然后互换arr[i]和arr[j]。然后再后移i，找到11，前移j，找到0，互换......重复以上步骤，直到i，j相遇，然后交换arr[i]和主元,得到主元在中，小的在左边，大的在右边的序列，然后对主元两侧的部分递归（类似归并）。

这里要留下一个问题：在题设条件下，可不可以先挪j再挪i？为什么？

如果主元选在第一个，那么应该先挪哪个？为什么？

代码实现：（自己写的，可能没那么快 bushi）

#include<stdio.h>
void change(int*x,int*y){
    int tmp=*x;
    *x=*y;
    *y=tmp;
}
void quick_sort(int* arr,int start,int end){
    if(start>=end) return;//递归出口
    if(end==start+1){
        if(arr[end]<arr[start]){
            change(&arr[start],&arr[end]);
        }
        return;
    }
    int i=start;int j=end;
    while(1){
        while(i<j&&arr[i]<=arr[end]){
            i++;
        }
        while(i<j&&arr[j]>=arr[end]){
            j--;
        }
        if(i>=j) break;
        change(&arr[i],&arr[j]);
    }
    change(&arr[i],&arr[end]);
    quick_sort(arr,start,i-1);
    quick_sort(arr,i+1,end);
}
int main(){
    int numsSize;
    scanf("%d",&numsSize);
    if(numsSize<=0) return 0x7fffffff;
    int arr[numsSize];
    for(int i=0;i<numsSize;i++){
        scanf("%d",&arr[i]);
    }
    quick_sort(arr,0,numsSize-1);
    for(int i=0;i<numsSize;i++){
        printf("%d ",arr[i]);
    }
}

这里我们研究快排的时间复杂度。快排就一定快吗？我们能否构建一种最坏情况？让快排变得很慢？其实是可以的。我们只需要让每次快排的主元（在上述情况下就是数组中最后面的值）取到整个数组的最大或者最小就好了。这样数组就无法“对半”或者“均匀”的切开，每次快排只能减少一个元素，就需要O(n)的递归深度。此时的时间复杂度就是O(n^n)。

对于这种情况，我们可以采取随机取主元的方法来解决这个问题。这里不再涉及。