吴恩达深度学习l2week1编程作业—Initialization

1、导入Packages

import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
from public_tests import *
from init_utils import sigmoid, relu, compute_loss, forward_propagation, backward_propagation
from init_utils import update_parameters, predict, load_dataset, plot_decision_boundary, predict_dec

%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

2、加载数据集

train_X, train_Y, test_X, test_Y = load_dataset()

3、神经网络模型

您将使用一个3层神经网络（已经为您实现）。下面是三种初始化方法：

Zeros initialization--在输入参数中设置initialization=“Zeros”
随机初始化——在输入参数中设置initialization=“Random”，这会将权重初始化为较大的随机值
He initialization--在输入参数中设置initialization=“he”

def model(X, Y, learning_rate = 0.01, num_iterations = 15000, print_cost = True, initialization = "he"):
"""
实现了一个三层神经网络：LINERAL->RELU->LINERAL-->RELU->LINEAR->SIGMOID
参数：
X——输入数据，形状（2，示例数）
Y——真正的“标签”矢量（包含0表示红点；1表示蓝点），形状（1，示例数）
learning_rate——梯度下降的学习率
num_iterrations—运行梯度下降的迭代次数
print_cost——如果为True，则每1000次迭代打印一次成本
initialization—用于选择要使用的初始化的标志（“zeros”、“random”或“he”）
返回：
parameters——模型学习的参数
"""
    grads = {}
    costs = [] # to keep track of the loss
    m = X.shape[1] # number of examples
    layers_dims = [X.shape[0], 10, 5, 1]

    # 初始化参数字典

    if initialization == "zeros":
        parameters = initialize_parameters_zeros(layers_dims)
    elif initialization == "random":
        parameters = initialize_parameters_random(layers_dims)
    elif initialization == "he":
        parameters = initialize_parameters_he(layers_dims)

    # Loop (gradient descent)

    for i in range(num_iterations):

        # Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
        a3, cache = forward_propagation(X, parameters)
        
        # Loss
        cost = compute_loss(a3, Y)

        # Backward propagation.
        grads = backward_propagation(X, Y, cache)
        
        # Update parameters.
        parameters = update_parameters(parameters, grads, learning_rate)
        
        # Print the loss every 1000 iterations
        if print_cost and i % 1000 == 0:
            print("Cost after iteration {}: {}".format(i, cost))
            costs.append(cost)
            
    # plot the loss

    plt.plot(costs)
    plt.ylabel('cost')
    plt.xlabel('iterations (per hundreds)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()
    
    return parameters

4、Zero Initialization

在神经网络中有两种类型的参数需要初始化：

Exercise 1 - initialize_parameters_zeros

def initialize_parameters_zeros(layers_dims):
"""
参数：
layer_dims——包含每层大小的python数组（列表）。

返回：
parameters——包含参数“W1”、“b1”…的python字典。。。，“WL”、“bL”：
W1——形状的权重矩阵（layers_dims[1]，layers_dims[0]）
b1——形状的偏置矢量（layers_dims[1]，1）
...
WL——形状的权重矩阵（layers_dims[L]，layers_dims[L-1]）
bL——形状的偏置矢量（layers_dims[L]，1）
"""
     parameters = {}
    L = len(layers_dims)            # number of layers in the network
    
    for l in range(1, L):

        parameters['W' + str(l)] = np.zeros((layers_dims[l],layers_dims[l-1]))
        parameters['b' + str(l)] = np.zeros((layers_dims[l],1))
        
    return parameters

parameters = initialize_parameters_zeros([3, 2, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
initialize_parameters_zeros_test(initialize_parameters_zeros)

运行以下代码，使用零初始化在15000次迭代中训练模型。

parameters = model(train_X, train_Y, initialization = "zeros")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)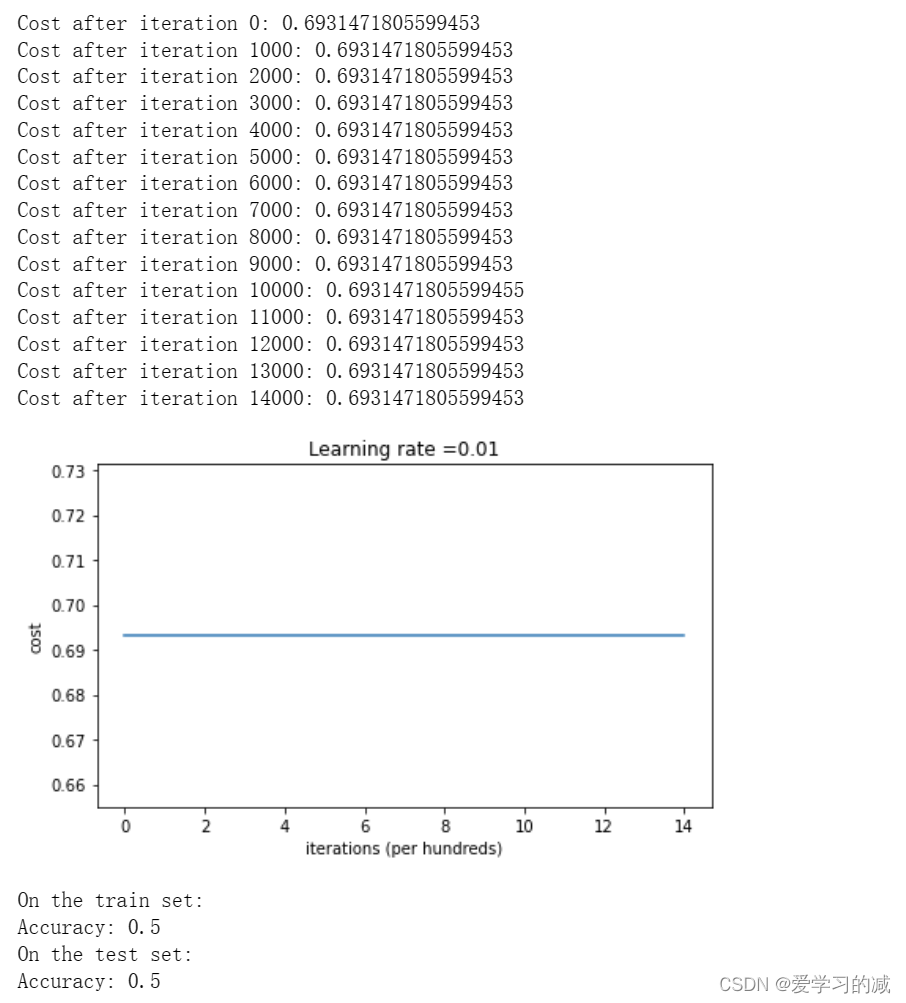

性能很糟糕，成本没有降低，而且算法的性能也不比随机猜测好。为什么？看看预测和决策边界的细节：

print ("predictions_train = " + str(predictions_train))
print ("predictions_test = " + str(predictions_test))

plt.title("Model with Zeros initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)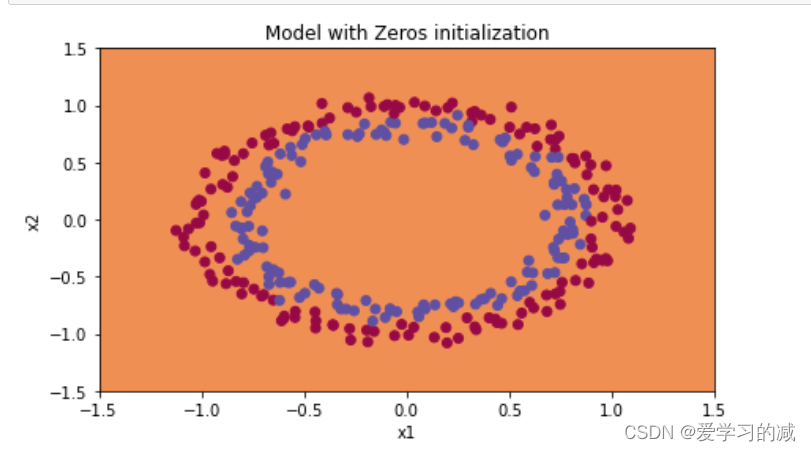

为了简单起见，下面的计算一次只使用一个例子。

由于权重和偏差为零，因此乘以权重会产生零向量，当激活函数为ReLU时，该向量为0。当z=0时

在分类层，激活函数为sigmoid，然后（对于任一输入）：

对于每个例子，你都有0.5的机会是真的，我们的成本函数在调整权重时变得无能为力。

损失函数：

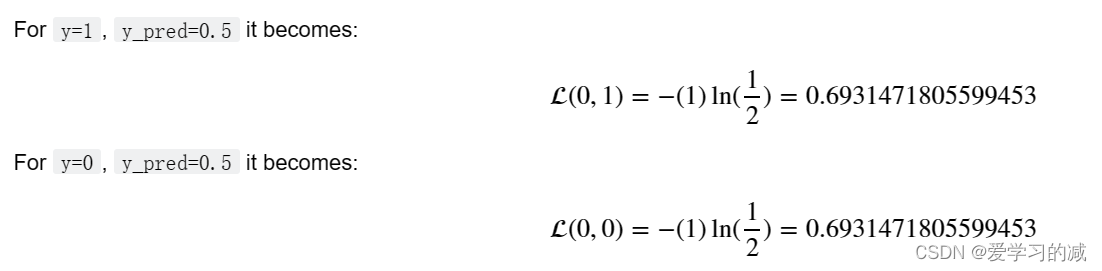
正如你所看到的，在预测为0.5的情况下，无论实际（y）值是1还是0，你都会得到相同的损失值，所以没有调整任何权重，你会使用相同的旧权重值。这就是为什么你可以看到模型对每个例子都预测为0！难怪它做得这么糟糕。通常，将所有权重初始化为零会导致网络无法破坏对称性。这意味着每一层中的每个神经元都会学习相同的东西，所以你也可以用𝑛[𝑙]=1.对于每一层。这样，网络并不比逻辑回归这样的线性分类器更强大。

下面是非常重要的内容！！！！

5、Random Initialization

若要破坏对称性，请随机初始化权重。在随机初始化之后，每个神经元可以继续学习其输入的不同函数。在本练习中，您将看到当权重被随机初始化但值非常大时会发生什么。

完善以下函数，将权重初始化为较大的随机值（按*10缩放），将偏差初始化为零。使用np.random.randn(...)*10初始化权重矩阵，使用np.zeros((.., ..))初始化偏置矩阵，我们使用np.random.seed(..)来保证我们的权重矩阵随机初始化后是一样的，所以多次运行代码后得到的随机矩阵都是相同的，不要担心。请完善如下函数：

Exercise 2 - initialize_parameters_random

def initialize_parameters_random(layers_dims):
    
    np.random.seed(3)               # This seed makes sure your "random" numbers will be the as ours
    parameters = {}
    L = len(layers_dims)            # integer representing the number of layers
    
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1])*10
        parameters['b' + str(l)] = np.zeros((layers_dims[l],1))
        
    return parameters

parameters = initialize_parameters_random([3, 2, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
initialize_parameters_random_test(initialize_parameters_random)

运行以下代码，使用随机初始化在15000次迭代中训练模型。

parameters = model(train_X, train_Y, initialization = "random")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)

如果您将“inf”视为迭代0之后的成本，这是因为数值舍入。一个更复杂的数字实现可以解决这个问题，但就本笔记本而言，这并不值得担心。

无论如何，您现在已经打破了对称性，这明显比以前提供了更好的准确性。该模型不再输出所有0!

print (predictions_train)
print (predictions_test)

plt.title("Model with large random initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

观察结果：

cost一开始很高，这是因为对于大的随机值权重，对于某些示例，最后一次激活（sigmoid）输出的结果非常接近0或1，并且当它弄错了该示例时，它会导致该示例的非常高的损失。事实上，当log(𝑎[3] ）=log（0），则损失无穷大。

初始化不良会导致梯度消失/爆炸，这也会减慢优化算法的速度。

如果你训练这个网络的时间更长，你会看到更好的结果，但用过大的随机数初始化会减慢优化速度。

高斯变量（numpy.random.randn（））和均匀随机变量之间的主要区别在于生成的随机数的分布：

random（）生成均匀分布的数字。

而numpy.random.randn（）生成正态分布中的数字。

当用于权重初始化时，randn（）有助于大多数权重避免接近极端，将大多数权重分配在范围的中心。

一种直观的方法是，例如，如果您使用sigmoid（）激活函数。

接近0或接近1的斜率非常小，所以接近这些极值的权重收敛到解的速度会慢得多，而将它们中的大部分放在中心附近会加快收敛速度。

6、He Initialization

最后，让我们试试"He initialization"，这是2015年以He等人的第一作者命名的（如果你听说过"Xavier initialization"，这与此类似，只是Xavier initialization对sqrt(1./layers_dims[l-1])的权重使用比例因子，其中初始化将使用sqrt(2./layers_dims[l-1])）
Exercise 3 - initialize_parameters_he

此函数类似于之前的initialize_parameters_random(...)函数，唯一的不同是前边将np.random.randn(..,..)乘上了10，而此处您将乘上（根号(2 / 上一层的维度)）。这是Heinitialization对具有ReLU激活层的建议。

def initialize_parameters_he(layers_dims):
    
    np.random.seed(3)
    parameters = {}
    L = len(layers_dims) - 1 # integer representing the number of layers
     
    for l in range(1, L + 1):
        
        parameters['W' + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1])*((2/layers_dims[l-1])**0.5)
        parameters['b' + str(l)] = np.zeros((layers_dims[l],1))

        
    return parameters

parameters = initialize_parameters_he([2, 4, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

initialize_parameters_he_test(initialize_parameters_he)

运行以下代码，使用He初始化在15000次迭代中训练模型。

parameters = model(train_X, train_Y, initialization = "he")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)

plt.title("Model with He initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

观察结果：

具有He初始化的模型在少量迭代中很好地分离了蓝点和红点。

7、总结

您已经尝试了三种不同类型的初始化。对于相同的迭代次数和相同的超参数，比较为：

8、回顾

不同的初始化会导致非常不同的结果

随机初始化用于打破对称性，确保不同的隐藏单元可以学习不同的东西

抵制初始化到太大的值！

He初始化适用于ReLU激活的网络