点的旋转变换

情形一（active or alibi transformation主动变换）

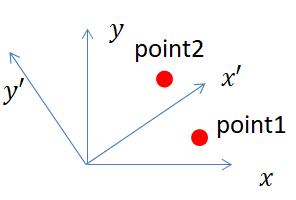
在坐标系$x?y$中，点$p_1$逆时针旋转$\alpha$后到达点$p_2$。
$p_1$在$x?y$中的表示与$p_2$在$x^{\prime }?y^{\prime }$中的表示一样，$x^{\prime }?y^{\prime }$为$x?y$旋转逆时针旋转$\alpha$后的新坐标系。
我们要求$p_2$在$x?y$中的表示？

（以下讨论均在$x?y$中）
$p_1^x=rcos\theta ,p_1^y=rsin\theta$
$p_2^x=rcos(\theta +\alpha ),p_2^y=rsin(\theta +\alpha )$
可以推出
$p_2^x=p_1^{x}cos\alpha ?p_1^{y}sin\alpha$
$p_2^y=p_1^{x}sin\alpha +p_1^{y}cos\alpha$
用矩阵表示
$A=\left[\begin{array}{cc}cos\alpha & ?sin\alpha \\ sin\alpha & cos\alpha \end{array}\right]$
$p_1=[p_1^x,p_1^y]$
$p_2=[p_2^x,p_2^y]$
$p_2=A{p}_1$

那么，假如我们已知$p_2$，我们要求$p_1$在$x?y$中的表示？
$p_1=A^{?1}{p}_2$
$A=\left[\begin{array}{cc}cos\alpha & sin\alpha \\ ?sin\alpha & cos\alpha \end{array}\right]$

情形二（passive or alias transformation被动变换）

https://en.wikipedia.org/wiki/Rotation_of_axes_in_two_dimensions

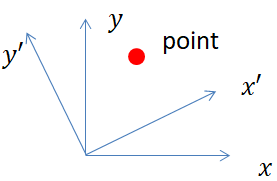
点$p$不动，$x^{\prime }?y^{\prime }$为$x?y$旋转逆时针旋转$\alpha$后的新坐标系。
我们已知$p$在$x?y$中的表示$[p^x,p^y]$，要求$p$在$x^{\prime }?y^{\prime }$中的表示$[p^{x^{\prime }},p^{y^{\prime }}]$？

$p^x=rcos\theta ,p^y=rsin\theta$
$p^{x^{\prime }}=rcos(\theta ?\alpha ),p^{y^{\prime }}=rsin(\theta ?\alpha )$
可以推出
$p^{x^{\prime }}=p^{x}cos\alpha +p^{y}sin\alpha$
$p^{y^{\prime }}=?p^{x}sin\alpha +p^{y}cos\alpha$
用矩阵表示
$A=\left[\begin{array}{cc}cos\alpha & sin\alpha \\ ?sin\alpha & cos\alpha \end{array}\right]$
$[p^{x^{\prime }},p^{y^{\prime }}{]}^T=A[p^x,p_1^y{]}^T$

那么，假如我们已知$p$在$x^{\prime }?y^{\prime }$中的表示$[p^{x^{\prime }},p^{y^{\prime }}]$，要求$p$在$x?y$中的表示$[p^x,p_1^y]$？
$[p^x,p_1^y{]}^T=A^{?1}[p^{x^{\prime }},p^{y^{\prime }}{]}^T$
$A^{?1}=\left[\begin{array}{cc}cos\alpha & ?sin\alpha \\ sin\alpha & cos\alpha \end{array}\right]$

主动变换与被动变换的变换矩阵一样？这说明要想让点$p_1$变换至$p_2$可通过主动绕原点旋转点$p_1$实现，也可以$p_1$不动但旋转坐标系来实现，两者虽然结果一样，但所处的坐标系不一样。