深度学习记录--正则化(regularization)

发布时间：2024年01月17日

什么是正则化？

正则化(regularization)是一种实用的减少方差(variance)的方法，也即避免过度拟合

几种正则化的方法

L2正则化

又被称为权重衰减(weight dacay)

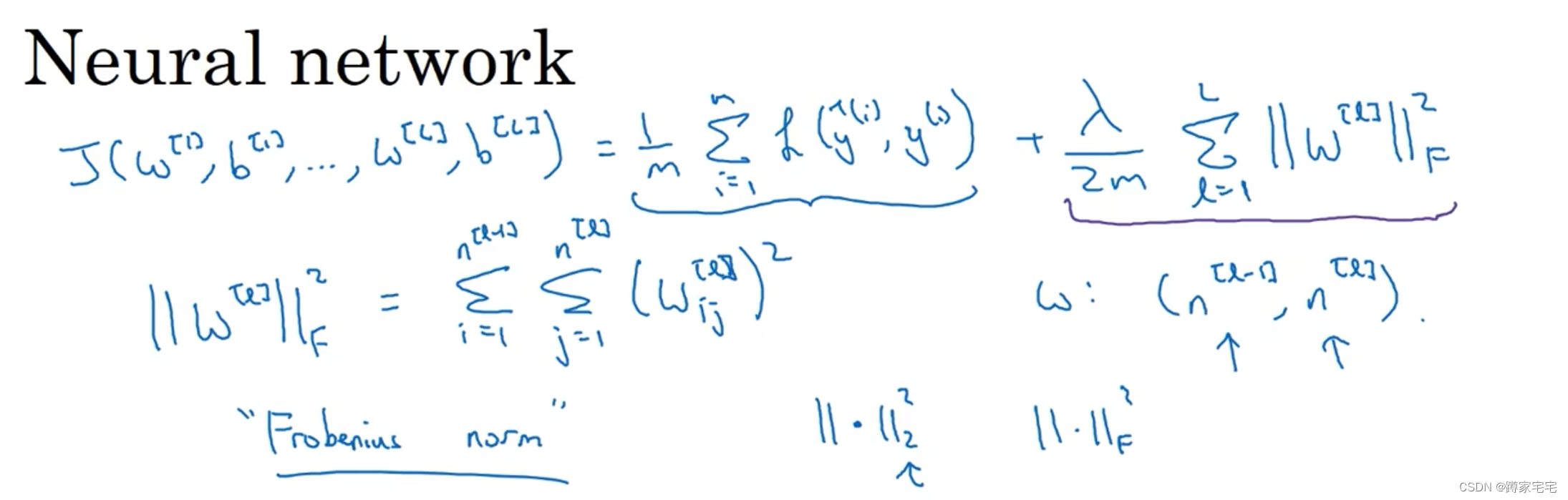
?在成本函数中加上正则项：

\frac{\lambda }{2m}\sum_{l=1}^{L}\left \| w^{\left [ l \right ]} \right \|^2_{F}

其中??\left \| x^{\left [ l \right ]} \right \|^2_{F}=\sum_{i=1}^{n^{\left [ l-1 \right ]}}\sum_{j=1}^{n^{\left [ l\right ]}}(w^{\left [ l \right ]}_{ij})^2?

?由于在w的更新过程中会递减，即权重衰减

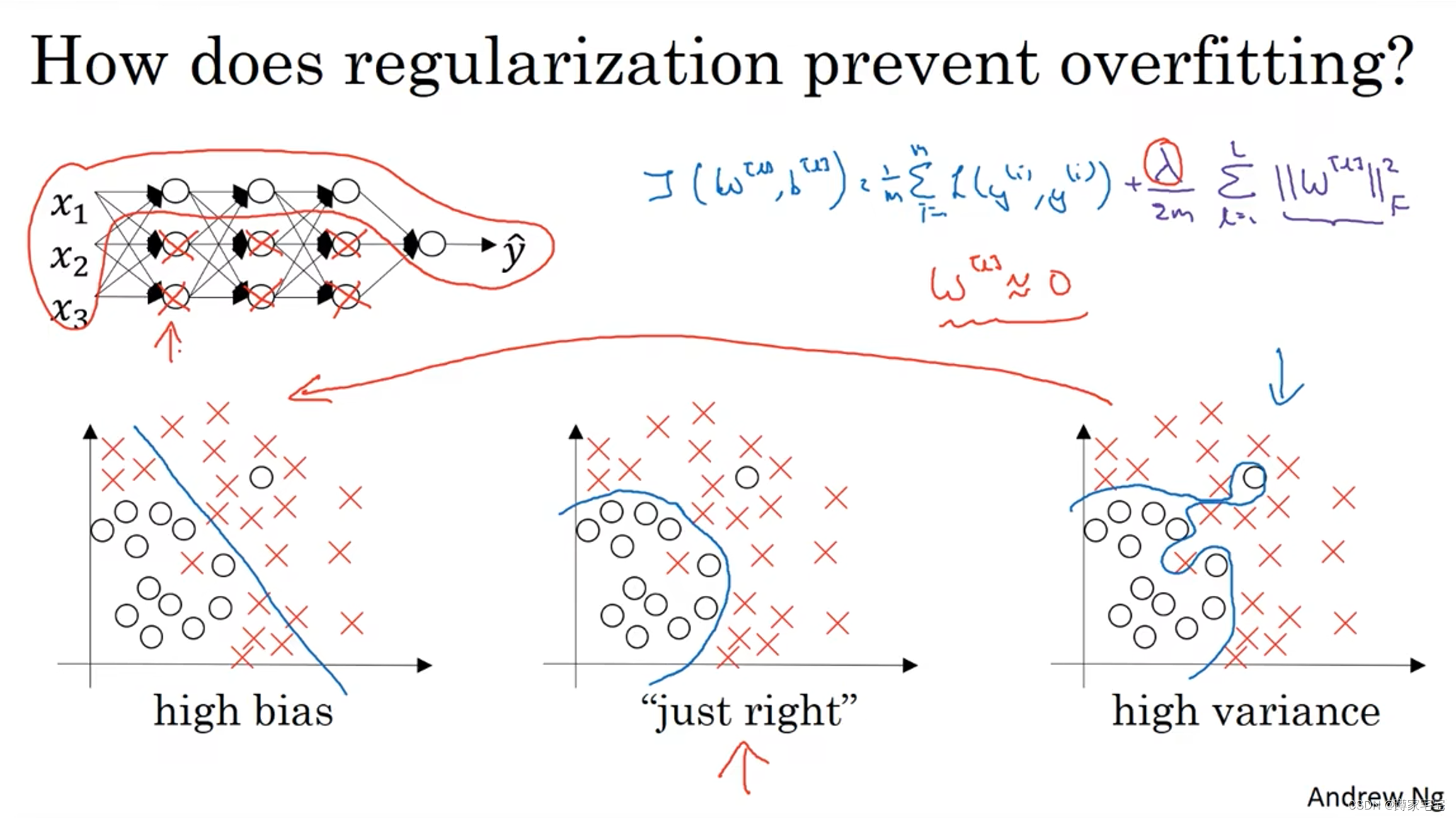
w^{\left [l \right ]}:= w^{\left [l \right ]}-\alpha dw^{\left [l \right ]}

w递减的过程，实际上是w趋近于0的过程

在这个过程中，部分单元的影响逐渐减小(可以近似看作隐藏)，最终成为深层神经网络(类似线性回归)，从最开始的右图逐渐变为左图，即从high variance --> high bias

在变化的中间存在一个just right的状态，这个状态则是最优情况

缺点：

为了搜索合适的正则化参数lambda，需要进行大量验证计算，花费时间很长

dropout(随机失活)

dropout基本原理：将神经网络中的部分单元进行随机删除/失活(将它们的影响降至几乎不存在)，让原本的神经网络样本训练规模变小

常用方法：inverted dropout(反向随机失活)

设置一个概率参数keep_prob，在例子中设置为0.8，表示有0.2的概率让单元失活

设置bool矩阵d3，将a3矩阵与d3矩阵进行矩阵乘法运算，然后a3/=keep_prob，保持未被失活单元的数据的完整性

代码实现：

import numpy as np
a3=np.random.rand(3,3)
print("before dropout : \n",a3)
keep_prob=0.8
# print(a3.shape[0],a3.shape[1])
d3=np.random.rand(a3.shape[0],a3.shape[1])<keep_prob
# print("d3 = ",d3)
a3=np.multiply(a3,d3)
a3/=keep_prob
print("after dropout : \n",a3)

运行结果：?

dropout合理性的解释

dropout会压缩权重(shrink weights)，完成预防过拟合的外层正则化(类似L2正则化的功能)，与L2正则化不同的是，dropout对不同的应用方式，会产生不同的效果

keep_prob的数值越小，dropout的效果越显著

对于某些层，若担心过拟合，可以设置更小的keep_prob参数值，而对于其他层，若无需使用dropout，则可以设置keep_prob=1

缺点

需要进行许多验证来得出不同的keep_prob参数值

同时，因为每次迭代部分节点都会被随机移除，J函数的定义无法被明确给出，难以对递减程度进行评估与复查

数据扩增data augmentation

当无法获得充足的数据时，又需要大量的数据时，则会选择这种方法：

对原有数据进行一定的处理，产生新的数据

缺点

需要额外的算法验证，对新数据判断是否合理

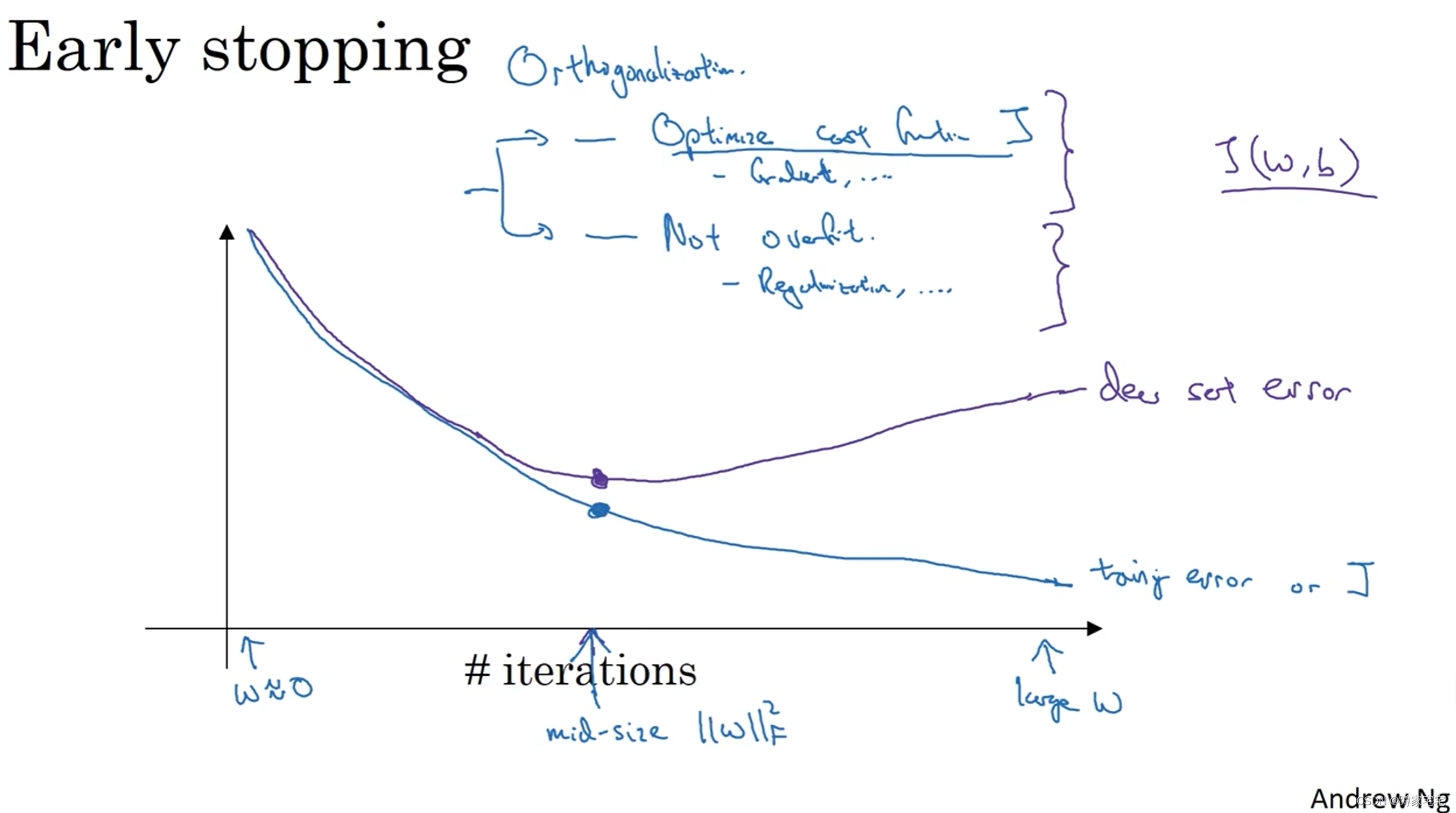
early stopping

只需运行一次梯度下降，找到w的较小值，中间值和较大值

在梯度下降过程中及时停止，得到较合理的dev set error和train set error

文章来源:https://blog.csdn.net/Xudong_12345/article/details/135594080
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章