双指针部分典型算法题（一）

????????可以通过一下几题加深一下对双指针思想的理解！对于一些问题我们一般可以通过快慢指针，或对撞指针来解决问题。

问题简述（1089. 复写零 - 力扣（LeetCode））：

class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        //找到最后一个复写的数
        int cur = 0; //cur指向的位置就是最后一个被复写的数
        int dest = -1;
        while(cur < arr.size()){
            if(arr[cur] != 0){
                dest++;
            } else{
                dest += 2;
            }
            //因为dest走的比cur快，我们还需要防止dest是否会越界
            if(dest >= arr.size()-1){
                break;
            }

            cur++;
        }

        //从后往前处理
        while(cur >= 0){
            if(arr[cur] != 0){ //cur指向元素不是零的话，将cur指向元素赋值给dest指向元素
                arr[dest--] = arr[cur--]; 
            } else{ //cur指向元素是零的话，需要把当前指向位置和前一个位置都置0
                arr[dest--] = 0;
                arr[dest--] = 0;
                cur--;
            }
        }
    }
};

提交运行发现未通过测试用例：

我们根据测试用例具体分析，可以找到最后一个复写的数的情况是：

当cur指向倒数第二个元素为0的时候，dest走两步刚好越界，所以我们需要额外做一步：

class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        //找到最后一个复写的数
        int cur = 0; //cur指向的位置就是最后一个被复写的数
        int dest = -1;
        while(cur < arr.size()){
            if(arr[cur] != 0){
                dest++;
            } else{
                dest += 2;
            }
            //因为dest走的比cur快，我们还需要防止dest是否会越界
            if(dest >= arr.size()-1){
                break;
            }

            cur++;
        }

        //当最后一个复写的数是0的时候，且这个位置在数组的倒数第二个元素时，dest会越界
        if(dest == arr.size()){
            arr[arr.size()-1] = 0; //只需要把最后一个元素置0，复写的那个0在数组之外不用管
            cur--;
            dest -= 2;
        }

        //从后往前处理
        while(cur >= 0){
            if(arr[cur] != 0){ //cur指向元素不是零的话，将cur指向元素赋值给dest指向元素
                arr[dest--] = arr[cur--]; 
            } else{ //cur指向元素是零的话，需要把当前指向位置和前一个位置都置0
                arr[dest--] = 0;
                arr[dest--] = 0;
                cur--;
            }
        }
    }
};

问题简述（202. 快乐数 - 力扣（LeetCode））：

?

在看这道题之前，我们可以先看一下这几个经典的问题

问题简述（202. 快乐数 - 力扣（LeetCode））：

?

对于这个典型的判环问题，我们可以使用快慢指针来解决，我们可以把他看成追击问题，快指针一次走两步，慢指针一次走一步，如果快指针和慢指针能相遇，那一定是由于链表中存在环。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != NULL && fast->next != NULL){
            fast = fast->next->next; //fast走两步
            slow = slow->next; //slow走一步
            if(slow == fast){ //快慢指针相遇
                return true;
            }
        }
        return false;
    }
};

? ? ? ? （1）那为什么慢指针和快指针一定会在环中相遇，而不是在环中错过呢？

证：假设慢指针在进环的时候和快指针的距离为N，每一次追击的时候慢指针走一步，快指针走两步，他们之间的距离变化为N-1，N-2，N-3，...，3，2，1，0，所以他们不会错过。

? ? ? ? （2）如果慢指针一次还是走一步，而快指针变为一次走三步呢？

证：假设慢指针在进环的时候和快指针的距离为N，每一次追击的时候慢指针走一步，快指针走两步，他们之间的距离变化为：

????????若N为偶数时，N-2，N-4，N-6，...，4，2，0

????????若N为奇数时，N-2，N-4，N-6，...，3，1，-1?

????????（其中，-1表示他们之间的距离会跟新为S-1，S为环长，环有几个结点，环长就为几）

所以，当N为偶数的时候表明，这一圈就能够追上，当N为奇数的时候表明，这一圈会错过，下一圈的时候距离更新为N = S-1，能否追上取决于N的奇偶性。

所以，这种情况下，我们可能追上，也可能永远追不上。

? ? ? ? （3）那我们可以在进一步的想，在慢指针走一步，快指针走两步的情况下，入环结点是在哪呢？问题简述（142. 环形链表 II - 力扣（LeetCode））：

我们可以假设：

? ? ? ? 链表头和入环结点距离为L，环长为S，入环结点到相遇点距离为X。

所以有，慢指针走的路程为：?

? ? ? ? ? ? ? ?快指针走的路程为：

? ?由?有

? ?所以我们可以推出，

cur指针从链表头开始走，走到入环点的距离为，此时cur停在了入环点，

再看slow指针，slow指针此时处于快慢指针相遇点处，当cur走到了入环点的时候，slow指针走的总路程是，带入等式?可化简为，所以此时的slow指针也正好在入环点，所以当cur指针和slow指针指向同一个结点时，这个点就是入环点。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        bool flag = false;
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != NULL && fast->next != NULL){
            fast = fast->next->next; //fast走两步
            slow = slow->next; //slow走一步
            if(slow == fast){ //快慢指针相遇
                flag = true;
                break;
            }
        }

        if(flag){
            ListNode* cur = head;
            while(cur != slow){
                slow = slow->next;
                cur = cur->next;
            }
            return slow;
        } else{
            return NULL;
        }
        
    }
};

同样的，我们可以根据给出的示例，具体推测：

?

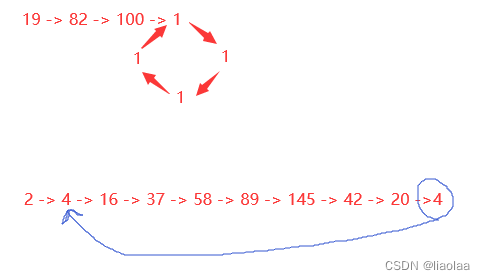在这里，我们的“快慢指针”分别是这些具体的数

class Solution {
public:
    int squareSum(int n){
        int sum = 0;
        while(n != 0){
            int t = n % 10;
            sum += t*t;
            n /= 10;
        }
        return sum;
    }

    bool isHappy(int n) {
        int slow = n; //slow指向第一个数
        int fast = squareSum(n); //fast指向第二个数
        while(slow != fast){
            slow = squareSum(slow);  //slow指针走一步
            fast = squareSum(squareSum(fast)); //fast指针走两步
        }
        return slow == 1;
    }
};