使用Pytorch搭建模型
本来是只用Tenorflow的,但是因为TF有些Numpy特性并不支持,比如对数组使用列表进行切片,所以只能转战Pytorch了(pytorch是支持的)。还好Pytorch比较容易上手,几乎完美复制了Numpy的特性(但还有一些特性不支持),怪不得热度上升得这么快。
1??模型定义
和TF很像,Pytorch也通过继承父类来搭建自定义模型,同样也是实现两个方法。在TF中是__init__()和call(),在Pytorch中则是__init__()和forward()。功能类似,都分别是初始化模型内部结构和进行推理。其它功能比如计算loss和训练函数,你也可以继承在里面,当然这是可选的。下面搭建一个判别MNIST手写字的Demo,首先给出模型代码:
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch import nn,optim
from torchsummary import summary
from keras.datasets import mnist
from keras.utils import to_categorical
device = torch.device('cuda') #——————1——————
class ModelTest(nn.Module):
def __init__(self,device):
super().__init__()
self.layer1 = nn.Sequential(nn.Flatten(),nn.Linear(28*28,512),nn.ReLU())#——————2——————
self.layer2 = nn.Sequential(nn.Linear(512,512),nn.ReLU())
self.layer3 = nn.Sequential(nn.Linear(512,512),nn.ReLU())
self.layer4 = nn.Sequential(nn.Linear(512,10),nn.Softmax())
self.to(device) #——————3——————
self.opt = optim.SGD(self.parameters(),lr=0.01)#——————4——————
def forward(self,inputs): #——————5——————
x = self.layer1(inputs)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x)
return x
def get_loss(self,true_labels,predicts):
loss = -true_labels * torch.log(predicts) #——————6——————
loss = torch.mean(loss)
return loss
def train(self,imgs,labels):
predicts = model(imgs)
loss = self.get_loss(labels,predicts)
self.opt.zero_grad()#——————7——————
loss.backward()#——————8——————
self.opt.step()#——————9——————
model = ModelTest(device)
summary(model,(1,28,28),3,device='cuda') #——————10——————
#1:获取设备,以方便后面的模型与变量进行内存迁移,设备名只有两种:‘cuda’和’cpu’。通常是在你有GPU的情况下需要这样显式进行设备的设置,从而在需要时,你可以将变量从主存迁移到显存中。如果没有GPU,不获取也没事,pytorch会默认将参数都保存在主存中。
#2:模型中层的定义,可以使用Sequential将想要统一管理的层集中表示为一层。
#3:在初始化中将模型参数迁移到GPU显存中,加速运算,当然你也可以在需要时在外部执行model.to(device)进行迁移。
#4:定义模型的优化器,和TF不同,pytorch需要在定义时就将需要梯度下降的参数传入,也就是其中的self.parameters(),表示当前模型的所有参数。实际上你不用担心定义优化器和模型参数的顺序问题,因为self.parameters()的输出并不是模型参数的实例,而是整个模型参数对象的指针,所以即使你在定义优化器之后又定义了一个层,它依然能优化到。当然优化器你也可以在外部定义,传入model.parameters()即可。这里定义了一个随机梯度下降。
#5:模型的前向传播,和TF的call()类似,定义好model()所执行的就是这个函数。
#6:我将获取loss的函数集成在了模型中,这里计算的是真实标签和预测标签之间的交叉熵。
#7/8/9:在TF中,参数梯度是保存在梯度带中的,而在pytorch中,参数梯度是各自集成在对应的参数中的,可以使用tensor.grad来查看。每次对loss执行backward(),pytorch都会将参与loss计算的所有可训练参数关于loss的梯度叠加进去(直接相加)。所以如果我们没有叠加梯度的意愿的话,那就要在backward()之前先把之前的梯度删除。又因为我们前面已经把待训练的参数都传入了优化器,所以,对优化器使用zero_grad(),就能把所有待训练参数中已存在的梯度都清零。那么梯度叠加什么时候用到呢?比如批量梯度下降,当内存不够直接计算整个批量的梯度时,我们只能将批量分成一部分一部分来计算,每算一个部分得到loss就backward()一次,从而得到整个批量的梯度。梯度计算好后,再执行优化器的step(),优化器根据可训练参数的梯度对其执行一步优化。
#10:使用torchsummary函数显示模型结构。奇怪为什么不把这个继承在torch里面,要重新安装一个torchsummary库。
2??训练及可视化
接下来使用模型进行训练,因为pytorch自带的MNIST数据集并不好用,所以我使用的是Keras自带的,定义了一个获取数据的生成器。下面是完整的训练及绘图代码(50次迭代记录一次准确率):
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch import nn,optim
from torchsummary import summary
from keras.datasets import mnist
from keras.utils import to_categorical
device = torch.device('cuda') #——————1——————
class ModelTest(nn.Module):
def __init__(self,device):
super().__init__()
self.layer1 = nn.Sequential(nn.Flatten(),nn.Linear(28*28,512),nn.ReLU())#——————2——————
self.layer2 = nn.Sequential(nn.Linear(512,512),nn.ReLU())
self.layer3 = nn.Sequential(nn.Linear(512,512),nn.ReLU())
self.layer4 = nn.Sequential(nn.Linear(512,10),nn.Softmax())
self.to(device) #——————3——————
self.opt = optim.SGD(self.parameters(),lr=0.01)#——————4——————
def forward(self,inputs): #——————5——————
x = self.layer1(inputs)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x)
return x
def get_loss(self,true_labels,predicts):
loss = -true_labels * torch.log(predicts) #——————6——————
loss = torch.mean(loss)
return loss
def train(self,imgs,labels):
predicts = model(imgs)
loss = self.get_loss(labels,predicts)
self.opt.zero_grad()#——————7——————
loss.backward()#——————8——————
self.opt.step()#——————9——————
def get_data(device,is_train = True, batch = 1024, num = 10000):
train_data,test_data = mnist.load_data()
if is_train:
imgs,labels = train_data
else:
imgs,labels = test_data
imgs = (imgs/255*2-1)[:,np.newaxis,...]
labels = to_categorical(labels,10)
imgs = torch.tensor(imgs,dtype=torch.float32).to(device)
labels = torch.tensor(labels,dtype=torch.float32).to(device)
i = 0
while(True):
i += batch
if i > num:
i = batch
yield imgs[i-batch:i],labels[i-batch:i]
train_dg = get_data(device, True,batch=4096,num=60000)
test_dg = get_data(device, False,batch=5000,num=10000)
model = ModelTest(device)
summary(model,(1,28,28),11,device='cuda')
ACCs = []
import time
start = time.time()
for j in range(20000):
#训练
imgs,labels = next(train_dg)
model.train(imgs,labels)
#验证
img,label = next(test_dg)
predicts = model(img)
acc = 1 - torch.count_nonzero(torch.argmax(predicts,axis=1) - torch.argmax(label,axis=1))/label.shape[0]
if j % 50 == 0:
t = time.time() - start
start = time.time()
ACCs.append(acc.cpu().numpy())
print(j,t,'ACC: ',acc)
#绘图
x = np.linspace(0,len(ACCs),len(ACCs))
plt.plot(x,ACCs)
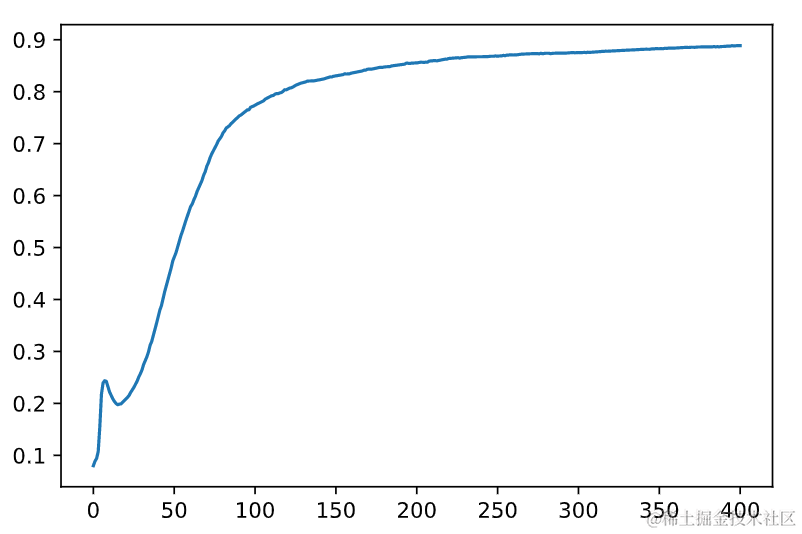
准确率变化图如下:
3??其它使用技巧
3.1??tensor与array
需要注意的是,pytorch的tensor基于numpy的array,它们是共享内存的。也就是说,如果你把tensor直接插入一个列表,当你修改这个tensor时,列表中的这个tensor也会被修改;更容易被忽略的是,即使你用tensor.detach.numpy(),先将tensor转换为array类型,再插入列表,当你修改原本的tensor时,列表中的这个array也依然会被修改。所以如果我们只是想保存tensor的值而不是整个对象,就要使用np.array(tensor)将tensor的值复制出来。
3.2??自定义层
在TF中,自定义模型通常继承keras的Model,而自定义层则是继承layers.Layer,继承不同的父类通常会造成初学者的困扰。而在pytorch中,自定义层与自定义模型一样,都是继承nn.Module。Pytorch将层与模型都看成了模块,这很容易理解。的确,层与模型之间本来也没有什么明确的界限。并且定义方式与上面定义模型的方式一样,也是实现两个函数即可。代码示例如下:
import torch
from torch import nn
class ParaDeconv(nn.Module):#——————1——————
def __init__(self,in_n,out_n):
super().__init__()
self.w = nn.Parameter(torch.normal(0,0.01,size = [in_n,out_n]),requires_grad=True)
self.b = nn.Parameter(torch.normal(0,0.01,size = [out_n]),requires_grad=True)
def forward(self,inputs):
x = torch.matmul(inputs,self.w)
x = x + self.b
return x
layer = ParaDeconv(2,3)
y = layer(torch.ones(100,2))#——————2——————
loss = torch.sum(y)#——————3——————
loss.backward()#——————4——————
for i in layer.parameters():#——————5——————
print(i.grad)#——————6——————
#1:自定义一个全连接层。层中可训练参数的定义是使用nn.Parameter,如果直接使用torch.tensor是无法在#5中遍历到的。
#2/3/4:输入并计算loss,然后反向传播计算参数梯度。
#5/6:输出完成反向传播后层参数的梯度。
以上定义的层可以和pytorch自带的层一样直接插入模型中使用。
3.3??保存/加载
3.3.1??保存/加载模型
有两种方式,一种是保存模型的参数:
torch.save(model.state_dict(), PATH) #保存
model.load_state_dict(torch.load(PATH),strict=True) #加载
这种加载方式需要先定义模型,然后再加载参数。如果你定义的模型参数名与保存的参数对不上,就会出错。但如果把strict修改成False,不严格匹配,它就会只匹配对应上的键值,不会因多出或缺少的参数而报错。
另一种是直接保存模型:
torch.save(model, PATH) #保存
model = torch.load(PATH) #加载
这种方式看似方便,实际上更容易出错。因为python不能保存整个模型的类,所以它只能保存定义类的代码文件位置,以在加载时获取类的结构。如果你改变了定义类的代码位置,就有可能因为找不到类而出错。
3.3.2??保存训练点
当你要保存某个训练阶段的状态,比如包含优化器参数、模型参数、训练迭代次数等,可以进行如下操作:
#保存训练点
torch.save({
'epoch': epoch,
'model_state_dict': model.state_dict(),
'optimizer_state_dict': optimizer.state_dict(),
'loss': loss
}, PATH)
#加载训练点
model = TheModelClass(*args, **kwargs)
optimizer = TheOptimizerClass(*args, **kwargs)
checkpoint = torch.load(PATH)
model.load_state_dict(checkpoint['model_state_dict'])
optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
epoch = checkpoint['epoch']
loss = checkpoint['loss']
和保存模型一样,也是使用torch.save()。它很灵活,可以保存字典,因此读取的时候也按照字典索引读取即可。当然要注意,并不是任何类型都能保存的,这里保存的四个类型分别是:
1. int
2.?collections.OrderedDict
3.?collections.OrderedDict
4. list
3.4??修改模型参数
Pytorch没有提供额外的方式让我们修改模型参数,我们可以使用上面加载模型参数的方式来修改参数。对于某个参数,我们只要把键值和对应要修改的值放在字典中传入load_state_dict即可。如果没传入所有的参数,记得把strict设为False。示例如下:
model.load_state_dict({'weight':torch.tensor([0.])},strict=False) #修改模型参数
参数名,也就是键值,和对应的参数shape可以通过model.state_dict()查看。
3.5??添加Grad Penalty (GP)
WGAN-GP的grad penalty需要用到二次求导,直接无脑使用backward()方法是不行的。梯度的计算有两种方法,一种是常见的backward(),另一种是autograd.grad()。
下面做一个简单的实验来记录如何使用这两者计算GP。代码如下:
import torch
from torch import nn, optim
from time import time
from torch import autograd
torch.manual_seed(1) #————0————
model = nn.Linear(3, 2) #————0————
opt = optim.SGD(model.parameters(), 0.1) #————0————
start_t = time()
for i in range(10):
x = torch.ones([1, 3], requires_grad=True) #————1————
y = torch.sum(model(x)) #————1————
# ***********************
y.backward(retain_graph = False, create_graph = True) #————2————
g = x.grad #————2————
# g = autograd.grad(y, x, retain_graph = False, create_graph = True)[0]
# ***********************
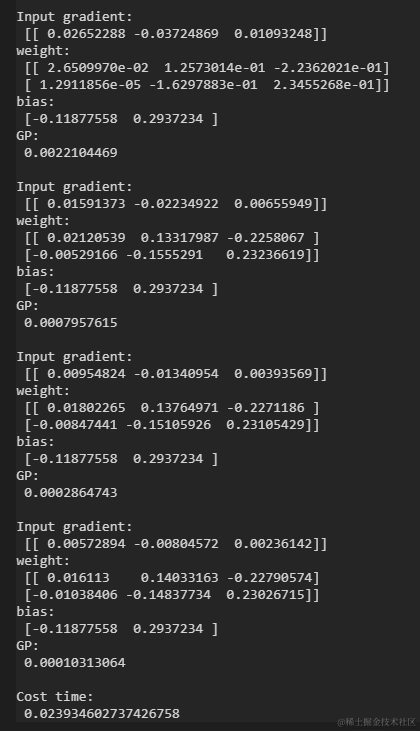
print("Input gradient: \n", g.detach().numpy())#————3————
for i in model.state_dict(): #————3————
print(i+":\n", model.state_dict()[i].numpy()) #————3————
gp = torch.sum(g**2) #————4————
print("GP: \n", gp.detach().numpy())
print()
opt.zero_grad() #————5————
gp.backward() #————5————
opt.step() #————5————
print("Cost time: \n", time() - start_t)
注释:
0、设置随机种子、创建只包含一个全连接层的模型(R3→R2R3→R2)、创建优化器。
1、定义可获取梯度的输入,并通过模型求得输出。
2、使用backward()或autograd.grad()获取输入关于输出的梯度。需要注意的是,create_graph = True 表示在反向传播计算梯度时记录计算图。因为梯度通常直接用来梯度下降,无需关于梯度的计算图,所以默认为False。而我们要用这个梯度再一次反向传播来计算Grad Penalty,所以需要设置为True。另外,retain_graph设置为False,表示计算完梯度后,关于模型输出的前向传播计算图就释放掉。因为我们需要的是输入关于输出的梯度的计算图,因此在获取梯度计算图之后,输入到输出的计算图就可以释放掉了。很多博客都设置为True,这是在浪费资源。
3、打印输入关于输出的梯度,并打印模型的权重值。可以验证,打印出的梯度向量值等于权重行向量之和。
4、计算GP。为了便于理解,这里直接用二范数的平方来代替。
5、使用GP更新模型权重。
输出结果如下:
可以看出权重两个行向量之和越来越接近0。这和数学计算的预期结果是一致的。
以上列举的两个方法,是有计算量上的差异的。backward()会计算所有与输出相关,且可获取梯度的参数的梯度;而autograd.grad()则只会计算输入与输出之间,与输入和输出都相关的梯度,且函数返回的只有输入关于输出的梯度。也就是说,在以上实验中,autograd.grad()不会计算全连接层中bias关于输出的梯度(因为它并没有影响到输入关于输出的梯度)。所以,使用autograd.grad()计算GP会更快。
我们可以使用以上代码进行实验,两种方法在10000次迭代中分别用时3.5s和3.2s,autograd.grad()快快了0.3秒。而这里的bias规模只有2,当规模大起来,节省的时间就很可观了。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- JavaScript中的this>构造函数/原型/垃圾回收机制
- linux 设备驱动之tty_driver数据结构介绍
- 【微服务核心】ZooKeeper
- vue3基础:单文件组件介绍
- R语言【cli】——ansi_toupper(),ansi_tolower():将ANSI彩色字符串全部大写或小写
- 用Gemini Pro 来做开发?API出来了
- C++11_14_17_20多线程
- 对接第三方的JSON形式数据转到 java 对应的实体类
- MR实战:学生信息排序
- 遥感图像分割系统:融合空间金字塔池化(FocalModulation)改进YOLOv8