C : DS二叉排序树之删除

Description

给出一个数据序列，建立二叉排序树，并实现删除功能

对二叉排序树进行中序遍历，可以得到有序的数据序列

Input

第一行输入t，表示有t个数据序列

第二行输入n，表示首个序列包含n个数据

第三行输入n个数据，都是自然数且互不相同，数据之间用空格隔开

第四行输入m，表示要删除m个数据

从第五行起，输入m行，每行一个要删除的数据，都是自然数

以此类推输入下一个示例

Output

第一行输出有序的数据序列，对二叉排序树进行中序遍历可以得到

从第二行起，输出删除第m个数据后的有序序列，输出m行

以此类推输出下一个示例的结果

Sample

#0

Input

1
6
22 33 55 66 11 44
3
66
22
77

Output

11 22 33 44 55 66 
11 22 33 44 55 
11 33 44 55 
11 33 44 55 

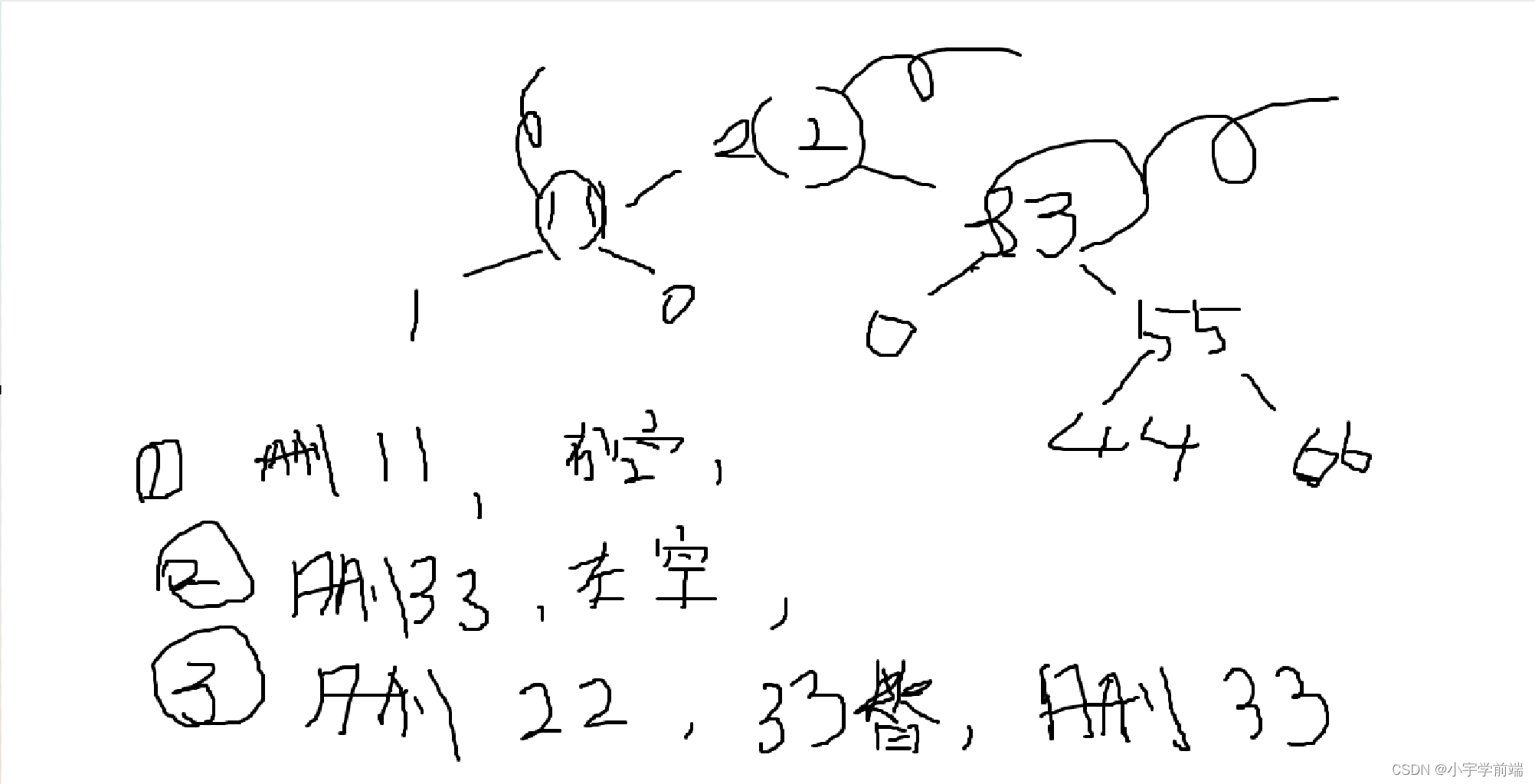
AC代码

#include <iostream>
using namespace std;

// 二叉排序树节点
struct TreeNode {
    int data;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};

// 插入节点到二叉排序树
TreeNode* insert(TreeNode* root, int data) {
    if (root == nullptr) {
        return new TreeNode(data);
    }

    if (data < root->data) {
        root->left = insert(root->left, data);
    }
    else {
        root->right = insert(root->right, data);
    }

    return root;
}

// 寻找最小值节点
TreeNode* findMin(TreeNode* node) {
    //不断往左树找，直到空为止就是最小的
    while (node->left != nullptr) {
        node = node->left;
    }
    return node;
}

// 删除节点
TreeNode* remove(TreeNode* root, int data) {
    if (root == nullptr) {
        return root;
    }

    // 不断寻找结点
    if (data < root->data) {
        root->left = remove(root->left, data);
    }
    else if (data > root->data) {
        root->right = remove(root->right, data);
    }
    else {
        // 节点找到
        //结点有一个或没有的情况
        if (root->left == nullptr) {
            //左手空，直接把右手接上
            TreeNode* temp = root->right;
            delete root;
            return temp;
        }
        else if (root->right == nullptr) {
            TreeNode* temp = root->left;
            delete root;
            return temp;
        }

        // 有两个子节点的情况
        // 去右手找到最小的结点
        TreeNode* temp = findMin(root->right);
        //用这个右手上找到的最小的来替换当前结点
        root->data = temp->data;
        //替换完了之后记得把temp删掉
        root->right = remove(root->right, temp->data);
    }
    return root;
}

// 中序遍历并输出结果
void inorderTraversal(TreeNode* root) {
    if (root != nullptr) {
        inorderTraversal(root->left);
        cout << root->data << " ";
        inorderTraversal(root->right);
    }
}

int main() {
    int t;
    cin >> t;

    for (int i = 0; i < t; ++i) {
        int n;
        cin >> n;

        TreeNode* root = nullptr;

        for (int j = 0; j < n; ++j) {
            int data;
            cin >> data;
            root = insert(root, data);
        }

        inorderTraversal(root);
        cout << endl;

        int m;
        cin >> m;

        for (int k = 0; k < m; ++k) {
            int deleteData;
            cin >> deleteData;
            root = remove(root, deleteData);
            inorderTraversal(root);
            cout << endl;
        }
    }

    return 0;
}