【论文笔记】Summarizing source code with Heterogeneous Syntax Graph and dual position
Summarizing source code with Heterogeneous Syntax Graph and dual position
Abstract
在本文中,我们提出了一个名为 HetSum 的新颖框架。具体来说,首先通过在 AST 中设计六种类型的增强边来构建异构语法图(HSG),这表明了源代码的异构结构。同时,考虑布局信息,为源代码中的每个标记设计了双重位置。此外,我们在 HetSum 中开发了异构图神经网络来对 HSG 进行编码,同时使用 Transformer 编码器提取代码布局特征。通过将学习到的代码标记向量同化到 HSG 编码器中,HetSum 可以捕获两个编码器之间的关系,以改进代码表示。为了便于生成高质量的摘要,我们在扩展 Transformer 解码子层的同时将复制机制集成到解码过程中。
1. Introduction
在生成高质量的代码摘要方法终仍存在一些局限性:
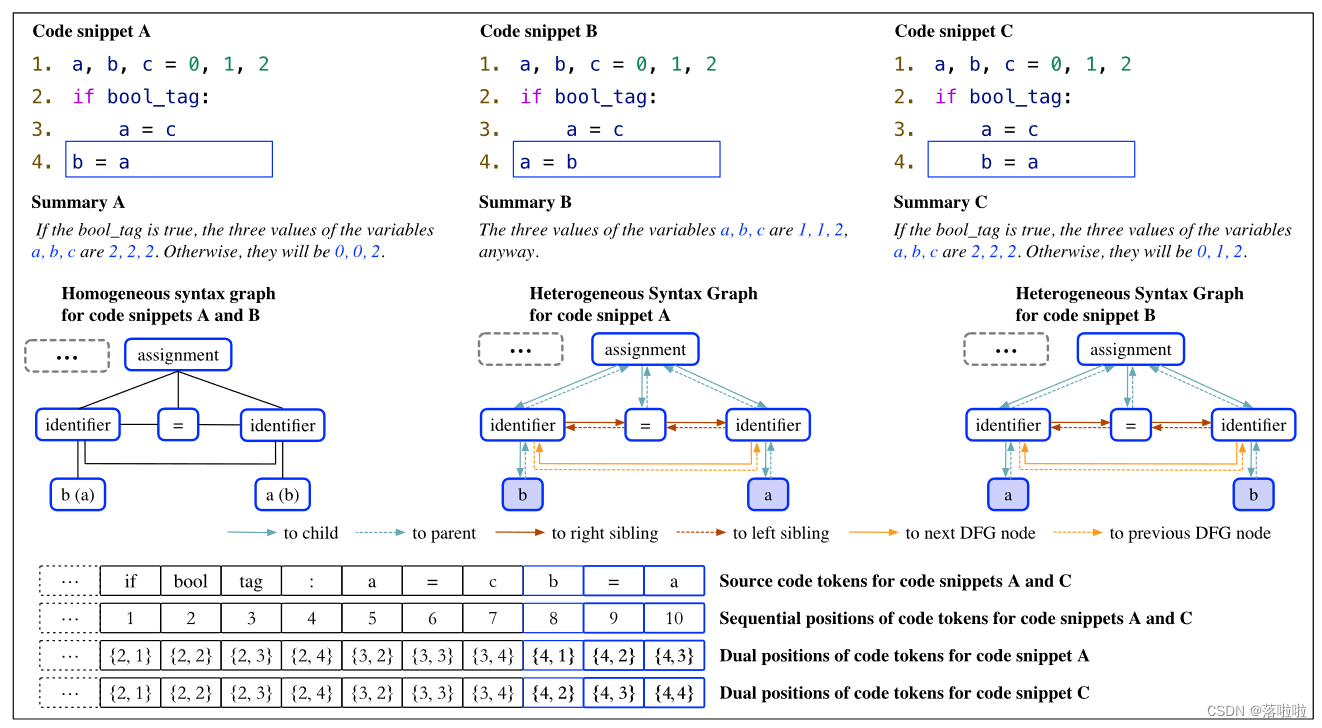
- AST 的异构性总是被忽略。在学习源代码的语法结构时,大多数基于 GNN 的模型仅将 AST 视为用于编码的同构图。我们认为 AST 的异构性对于保持 AST 的结构独特性至关重要,如图 下图所示,代码片段 A 和 B 通过在 AST 上添加数据流边和兄弟边而具有相同的同构语法图,因为节点 ‘’=‘’ 无法通过同构边区分其右兄弟节点’‘identifier’’ 和左兄弟节点 ‘‘identifier’’ 。事实上,节点 ‘’=‘’ 也无法区分其父节点 ‘‘assignment’’ 和兄弟节点 ‘‘identifier’’ 。因此,边的同构性削弱了 GNN 识别节点之间不同关系的学习能力。
- 源代码标记的位置信息尚未得到很好的研究。迄今为止,那些将源代码编码为纯文本的方法忽略了代码的布局信息,该信息记录了代码标记的精确位置。例如,下图中的代码片段A和C被处理成具有相同顺序位置的相同标记序列,导致它们无法被类似Transformer的模型区分。
解决方法:
- 鉴于上述限制,本文首先将基于 AST 的同构图扩展为具有六种有向边的异构语法图(HSG)。具体地,来自HSG中的节点的边可以到达其子节点、父节点、右兄弟节点、左兄弟节点、下一个DFG节点或前一个DFG节点,这可以很好地保留HSG的结构唯一性。例如,由于节点 ‘’=‘’ 和它的两个兄弟节点(‘‘identifier’’)之间的有向边,上图 中代码片段 A 和 B 的 HSG 是不同的。此外,不同的边类型使得节点 ‘’=‘’ 区分其父节点 ‘‘assignment’’ 和兄弟节点。
- 为了保留源代码的布局信息,我们为原始源代码中的每个代码标记设计了双重位置。通过双重位置,代码令牌可以通过行号和该行中的顺序位置精确定位。例如,上图中的双重位置突出显示了代码片段 A 和 C 之间的布局差异。
2. HSG and dual position
2.1 HSG construction
为了获取给定代码片段的 HSG,我们首先将其解析为 AST。作为源代码的基本层次语法结构,AST仅表示其节点之间的父子关系。因此,为了进一步丰富 AST 节点之间的关系,我们将 AST 增强为同构语法图。在这个阶段,我们在所有兄弟节点之间引入边来表示兄弟关系。此外,我们引入额外的边来构造数据流图(DFG),用来表示数据流。 DFG 指示每个变量来自或去往何处,可以进一步捕获数据依赖性以实现更好的代码表示。例如,在图 1 中的同构语法图中,节点 “=” 通过三个边连接到其两个兄弟节点 ‘‘identifier’’ 和父节点’‘assignment’’ 。此外,两个 ‘‘identifier’’ 节点之间存在数据依赖性。应该注意的是,所有节点实际上都无法通过这些同构边区分其父节点、子节点、兄弟节点和 DFG 邻居节点。
第二步,我们从同构语法图构建 HSG。我们将同构语法图中的边改进为具有方向的异构边。如图 1 中的 HSG 所示,节点的边可能通向其子节点、父节点、右兄弟节点、左兄弟节点、下一个 DFG 节点或前一个 DFG 节点。在本文中,我们定义从当前节点到其下一个DFG节点的边意味着当前节点的数据流向其下一个DFG节点。相反,从当前节点到其前一个DFG节点的边表示当前节点的数据来自其前一个DFG节点。通过明确指定六种类型的边,精确识别节点之间的对应关系,从而很好地保持了HSG的结构唯一性。例如,在代码片段 A 的 HSG 中,左侧 ‘‘identifier’’ 可以准确识别其子节点 “b”、父节点’‘assignment’'、右侧兄弟节点 “=” 以及前一个 DFG 节点 ‘‘identifier’’。
2.2 Code tokens with dual positions
由于自动代码摘要生成严重依赖于源代码标记,因此我们将原始源代码及其 HSG 结合起来,生成具有双重特征的代码标记。增强代码标记表示的位置。为此,首先遍历 HSG 以获取与标记化源代码相关的所有叶节点。与早期将源代码视为自然语言中的纯文本的方法不同,我们考虑了通过为每个代码标记呈现双重位置来显示代码布局信息。双重位置是由两个值组成的元组。第一个值记录行号,第二个值指示当前行中的顺序位置。两个值都从 1 开始。特别是,源代码中的缩进被认为具有连续位置,尽管它不被视为代码标记。例如,在图 1 中,令牌 “c” 的双重位置 {3, 4} 表示考虑到行开头的缩进,该令牌位于第三行的第四个位置。通过指定这样的双重位置,所有代码标记都具有与源代码对应的精确位置信息,这可以保持源代码的布局唯一性,以实现更好的代码表示。
3. HetSum model
3.1 Overview
假设将源代码片段表示成一个 HSG,这个 HSG 具有 l n l_n ln? 个节点表示为 T n = ( n 1 , n 2 , . . . , n l n ) T_n = (n_1, n_2, ... , n_{l_n} ) Tn?=(n1?,n2?,...,nln??),还有 l c l_c lc? 个代码 token 表示为 T c = ( c 1 , c 2 , . . . , c l c ) T_c = (c_1, c_2, ... , c_{l_c} ) Tc?=(c1?,c2?,...,clc??) 以及具有双重位置表示为 P c = ( { x 1 , y 1 } , { x 2 , y 2 } , . . . , { x l c , y l c } ) P_c = ( \{x_1, y_1\}, \{x_2, y_2\}, ... , \{x_{l_c} , y_{l_c} \}) Pc?=({x1?,y1?},{x2?,y2?},...,{xlc??,ylc??})。基于当前代码摘要的标记表示为 T s = ( ? ∕ s t a r t ? , s 1 , s 2 , . . . , s m ? 1 , ? ∕ p a d ? , ? ∕ p a d ? , . . . ) T_s = (?∕start?, s_1, s_2, ... , s_{m?1}, ?∕pad?, ?∕pad?, ...) Ts?=(?∕start?,s1?,s2?,...,sm?1?,?∕pad?,?∕pad?,...) ,其具有连续位置 P s = ( 1 , 2 , . . . , l s ) P_s = (1, 2 , ... , l_s) Ps?=(1,2,...,ls?),HetSum 尝试通过融合从 HSG 和代码标记中提取的特征来生成下一个摘要标记 s m s_m sm?。请注意, ? ∕ s t a r t ? ?∕start? ?∕start? 是初始化 T s T_s Ts? 的特殊标签, ? ∕ p a d ? ?∕pad? ?∕pad? 用于将 T s T_s Ts? 填充到 HetSum 输入的长度 l s l_s ls?。
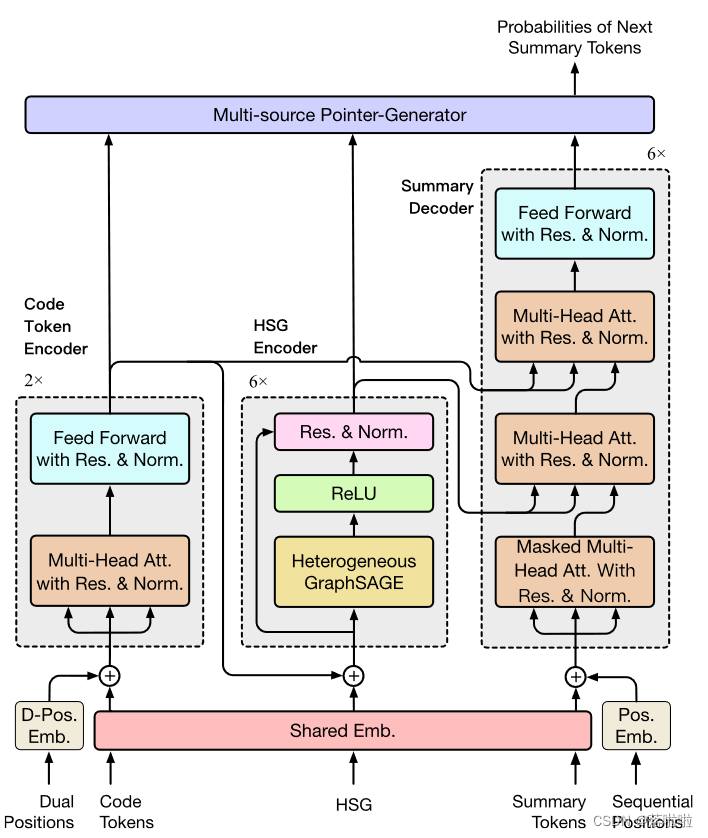
图 2 说明了所提出的 HetSum 的框架。它主要由三个组件组成:Code Token Encoder、HSG Encoder 和具有复制机制的 Summary Decoder。在编码过程中,双位置代码标记和 HSG 分别地流入Transformer编码器和 HSGNN 层,用于获取代码标记表示 E c ′ ∈ R l c × d E^′_c ∈ R^{l_c×d} Ec′?∈Rlc?×d 和语法图表示 E n ′ ∈ R l n × d E^′_n ∈ R^{l_n×d} En′?∈Rln?×d ,其中 d d d 是嵌入大小。随后,HetSum 执行具有复制机制的基于 Transformer 的解码器,将现有摘要标记作为输入,并融合提取的代码标记和 HSG 特征(即 E c ′ E^′_c Ec′? 和 E n ′ E^′_n En′?),以预测生成摘要的下一个标记 s m s_m sm? 。
3.2 Embeddings
在对代码标记、HSG 和摘要文本进行编码之前,需要将它们转换为数值向量。在本研究中,HSG 节点 T n T_n Tn? 直接映射到嵌入向量 E n 0 ∈ R l c × d E^0_n ∈ R^{l_c×d} En0?∈Rlc?×d 中。通过利用可学习的位置嵌入,代码标记 T c T_c Tc? 和摘要标记 T s T_s Ts? 被转换为向量 E c 0 ∈ R l c × d E^0_c ∈ R^{l_c×d} Ec0?∈Rlc?×d 和 E s 0 ∈ R l c × d E^0_s ∈ R^{l_c×d} Es0?∈Rlc?×d,分别包含他们的双重位置 P c P_c Pc? 和顺序位置 P s P_s Ps?。三个嵌入过程的公式如下:
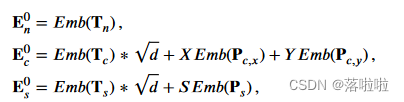
其中 E m b Emb Emb 表示 T n 、 T c T_n、T_c Tn?、Tc? 和 T s T_s Ts? 的共享嵌入操作; P c , x = ( x 1 , x 2 , . . . , x l c ) P_{c,x} = (x_1, x_2, ... , x_{l_c} ) Pc,x?=(x1?,x2?,...,xlc??) 和 P c , y = ( y 1 , y 2 , . . . , y l c ) P_{c,y} = (y_1, y_2, ... , y_{l_c} ) Pc,y?=(y1?,y2?,...,ylc??) 是双重位置 P c P_c Pc? 的分量。 X E m b XEmb XEmb、 Y E m b Y Emb YEmb 和 S E m b SEmb SEmb 对应于位置嵌入操作。
3.3. Code token encoder
图2描绘了Code token 编码器包括两个相同的Transformer层。每层都由多头注意力机制以及全连接的位置前馈网络组成,两者都遵循残差连接和层归一化。残差链接用来缓解多层计算中的梯度消失问题。层归一化可以减轻残差连接期间过多的矢量偏移。第k个Code token编码层的整个流程表述如下:
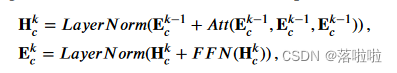
其中 E c k ? 1 ∈ R l c × d E^{k-1}_c ∈ R^{l_c×d} Eck?1?∈Rlc?×d 表示上一层输出的向量; F F N F F N FFN 表示前馈网络; L a y e r N o r m LayerNorm LayerNorm 表示层归一化; A t t Att Att 表示多头注意力。前馈网络包含两个由非线性变换的 ReLU 激活分隔的线性变换,其公式如下:
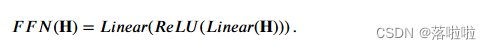
3.4 HSG encoder
鉴于 GraphSAGE 在处理图时的高效率和性能,我们通过改进 GraphSAGE 用于 HSG 表示学习的思想来开发 HSGNN。如图2所示,HSG编码器包括六个相同的HSGNN层。需要强调的是,学习到的代码标记表示被设计为在将 HSG embeddings 放入第一个 HSGNN 层之前集成到 HSG embeddings 中,以对代码标记编码器和 HSG 编码器之间的关系进行建模。为此,对于源代码中的每个 HSG 叶节点及其对应的标记,学习到的代码标记向量将被添加到 HSG 叶嵌入向量中。
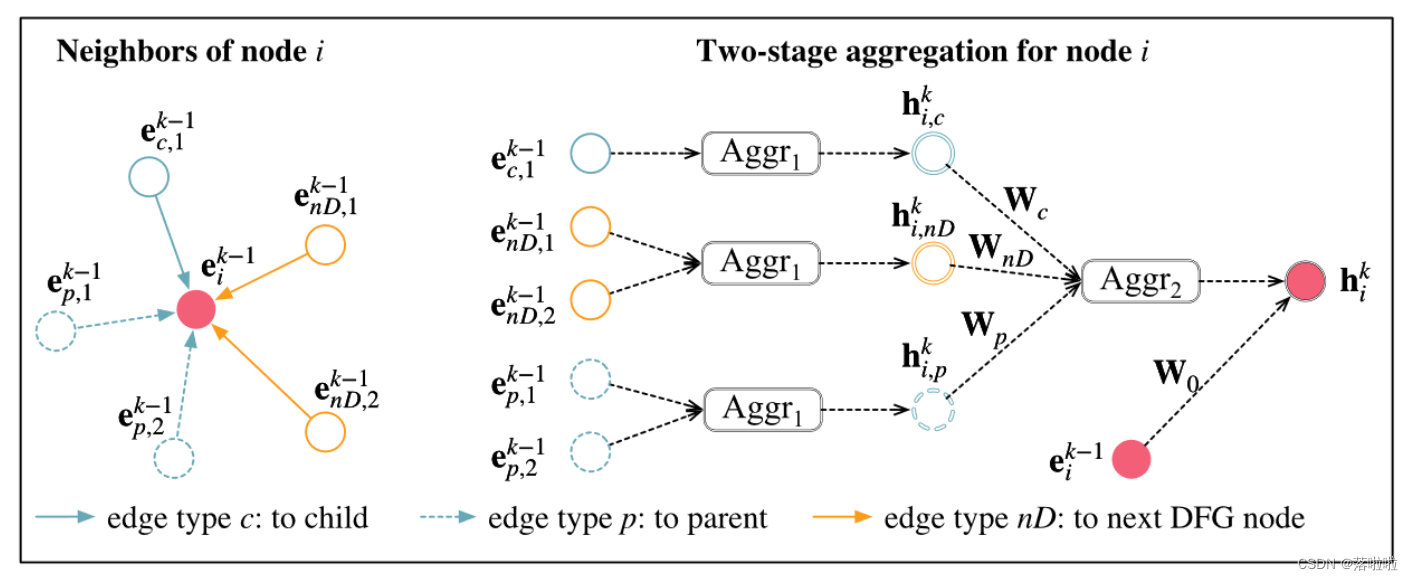
在第 k 个 HSGNN 层中,HSG 首先由异构 GraphSAGE 处理。具体来说,对于 HSG 节点 i i i,它的状态通过指向该节点的邻居节点的两个阶段聚合来更新,如图 3 所示。在第一阶段,具有不同边类型的邻居分别被聚合为不同的邻居组。对于边类型 g,聚合公式为:
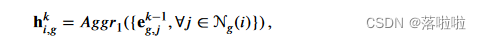
其中 N g ( i ) N_g(i) Ng?(i) 表示边类型为 g g g 的节点 i i i 的邻居; e g , j k ? 1 ∈ R d e^{k?1}_{g,j} ∈ R^d eg,jk?1?∈Rd 表示第 ( k ? 1 ) (k?1) (k?1) 层、边类型为 g g g 的第 j j j 个邻居的向量; A g g r 1 Aggr_1 Aggr1? 表示聚合函数。在第二阶段,转换和聚合邻居组以更新节点的状态,其公式如下:
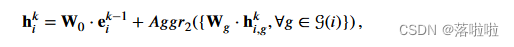
其中 e i k ? 1 ∈ R d e^{k?1}_{i} ∈ R^d eik?1?∈Rd 表示上一个 HSGNN 层输出的节点 i i i 的向量; g ( i ) g(i) g(i)表示通向节点 i i i 的边的类型; A g g r 2 Aggr_2 Aggr2? 表示聚合函数; W 0 , W g ∈ R d × d W_0, W_g ∈ R^{d×d} W0?,Wg?∈Rd×d 是可学习的权重矩阵。
一旦节点状态全部更新,状态向量就会被连接起来并输入到 R e L U ReLU ReLU 激活函数中进行非线性变换,其公式如下:
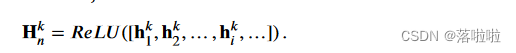
通过更多堆叠的 HSGNN 层,节点可以从更远的距离收集其相邻数据,从而捕获更多异构结构特征。为了减轻多层计算导致的梯度消失和过多的向量偏移,我们在每一层中采用残差连接以及层归一化,其公式为以下:
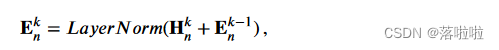
其中方程中的 E k ? 1 ∈ R l n × d E^{k?1} ∈ R^{l_n×d} Ek?1∈Rln?×d 表示第 ( k ? 1 ) (k?1) (k?1) 个 HSGNN 层输出的 HSG 节点向量。
3.5 Summary decoder
为了利用学习到的代码标记和 HSG 表示来生成摘要,我们通过实现六层扩展 Transformer 解码模块来设计 HetSum 的解码器。每个模块包含四个子层:一个用于自注意力编码的屏蔽多头注意力子层,两个用于两阶段解码的多头注意力子层,以及一个用于非线性变换的 F F N F F N FFN 子层。每个子层后面都是带有层归一化的残差连接。
给定现有的摘要标记,解码器首先基于屏蔽多头注意力对其进行解码。
之后,通过与两个编码器交互,堆叠两个多头注意力模块,基于现有的摘要标记进行两阶段解码。一个模块处理学习到的 HSG 表示以获得第一阶段解码信息,随后将其放入第二阶段解码模块,该模块吸收提取的代码标记特征。接下来, F F N F F N FFN 子层将解码后的向量作为非线性变换的输入。整个过程表述如下:
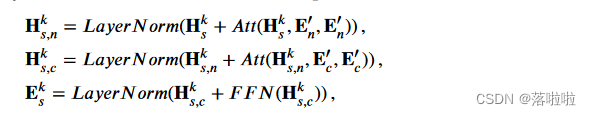
其中 E c ′ ∈ R l c × d E^′_c ∈ R^{l_c×d} Ec′?∈Rlc?×d 和 E n ′ ∈ R l n × d E^′_n ∈ R^{l_n×d} En′?∈Rln?×d 分别表示提取的 HSG 和代码 token 的特征。
3.6. Copying mechanism
由于许多代码标记(例如变量和函数名称)可能存在于文本摘要和源代码中,我们根据编码器和解码器实现了复制机制多源指针生成器(MPG)网络,最终确定后续的摘要标记。基于多头注意力,MPG 允许 HetSum 生成更准确的摘要标记,这些标记都是在词汇表中选择的,并且是从输入 HSG 节点和源代码标记复制的。
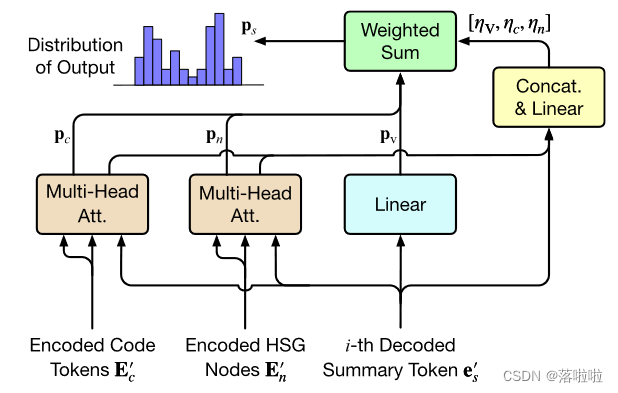
如上图所示,为了生成第 i i i 个摘要标记的输出似然,MPG 首先计算对应于摘要词汇表、代码标记和 HSG 节点的三个概率分布 p v p_v pv?、 p c p_c pc? 和 p n p_n pn?。 p v pv pv 是通过在解码的摘要标记向量 e ′ s ∈ R d e′_s ∈ Rd e′s?∈Rd 上执行 S o f t m a x Softmax Softmax 的 L i n e a r Linear Linear 子层导出的,其定义如下:

如果候选标记 w w w 不在摘要词汇表中,则 p v ( w ) p_v(w) pv?(w) 设置为 0。
p c p_c pc? 和 p n p_n pn? 是基于摘要解码器以及代码令牌和 HSG 编码器上的两个附加多头注意力子层计算的。具体来说, p c p_c pc? 是根据第 i i i 个解码后的摘要标记向量 e ′ s e′_s e′s? 和编码后的代码标记 E ′ c E′_c E′c? 进行 s o f t m a x softmax softmax 注意力值得出的,其公式如下:

其中 w j w_j wj? 表示第 j j j 个源代码标记; a ˉ c ∈ R l c \bar{a}_c ∈ R^{l_c} aˉc?∈Rlc? 表示注意力值。如果 w w w 不是代码标记,则 p c ( w ) = 0 p_c (w) = 0 pc?(w)=0。具体来说,MPG 中的注意力子层以 e ′ s e′_s e′s? 作为查询,以 E ′ c E′_c E′c? 作为键和值来得到 a ˉ c \bar{a}_c aˉc?,其公式如下:
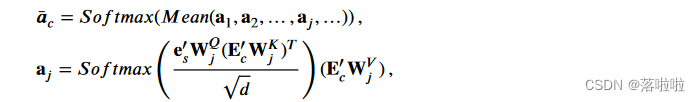
其中 W j Q W^Q_j WjQ?、 W j K W^K_j WjK? 和 W j V W^V_j WjV? 是可训练矩阵。此外,上下文向量 θ c ∈ R d θ_c ∈ R^d θc?∈Rd 对于下一个摘要标记的最终输出似然至关重要,计算如下:
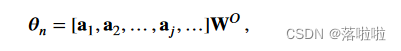
其中 W O W^O WO 表示可训练参数, a j a_j aj? 来自上式
p n p_n pn? 和 θ n θ_n θn? 的计算过程与 p c p_c pc? 和 θ c θ_c θc? 的计算过程相同,唯一的区别是 p n p_n pn? 和 θ n θ_n θn? 的多头注意力中的 key 和 value 是编码后的 HSG E ′ n E′_n E′n?。最后,候选标记 w w w 的似然 p s ( w ) p_s(w) ps?(w) 定义为三个概率 p v 、 p c p_v、p_c pv?、pc? 和 p n p_n pn? 的加权和:
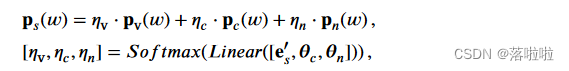
其中 η v 、 η c η_v、η_c ηv?、ηc? 和 η n η_n ηn? 表示对应于 p v 、 p c p_v、p_c pv?、pc? 和 p n p_n pn? 的权重。理论上,标记 w w w 更有可能被视为具有较高概率 p s ( w ) p_s(w) ps?(w) 的下一个摘要标记。
4. Experiment
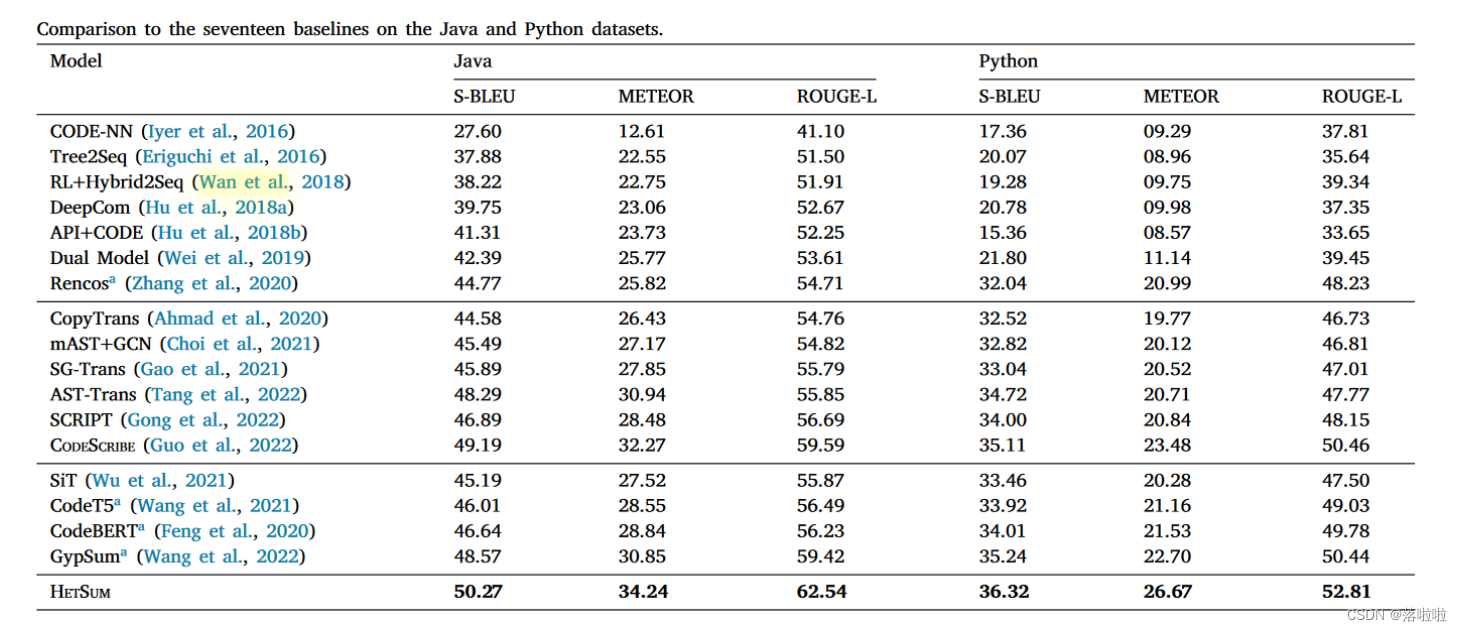
4.1 Experimental results
4.2 Ablation study
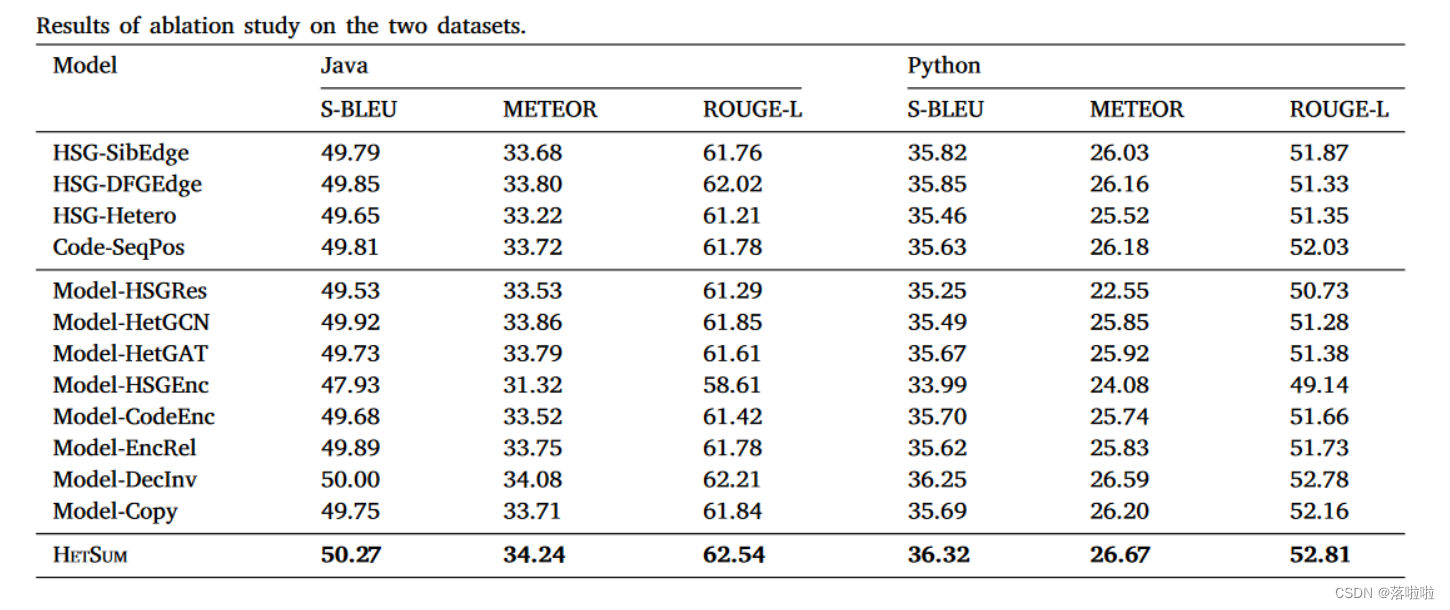
首先设计了四种变体模型来验证 HSG 的异构结构特征和源代码中的布局信息:
- HSG-SibEdge,排除HSG中兄弟节点之间的边
- HSG-DFGEdge,排除HSG中的DFG
- HSG-Hetero,忽略HSG中的异构性,使用同构GraphSAGE进行语法结构学习
- Code-SeqPos,将源代码标记视为先前工作中的自然语言序列,并将双重位置替换为顺序位置。
为了进一步研究HetSum模型架构的合理性,我们构建了八个变体:
- 模型-HSGRes,消除了HSG编码器中层归一化的残差连接
- 模型-HetGCN,用GCN替换HSGNN中使用的GraphSAGE
- Model-HetGAT 引入 GAT 以取代 HSGNN 中的 GraphSAGE
- Model-HSGEnc 删除 HSG 编码器
- Model-CodeEnc删除代码令牌编码器
- Model-EncRel,不将编码的代码令牌集成到 HSG 嵌入中,以丢弃两个编码器之间的关系
- Model-DecInv,反转 HSG 和代码令牌特征的解码在摘要解码器中
- 删除复制机制的模型复制。
请注意,GrapSAGE、GCN 和 GAT 都是常用于图学习任务的典型 GNN。
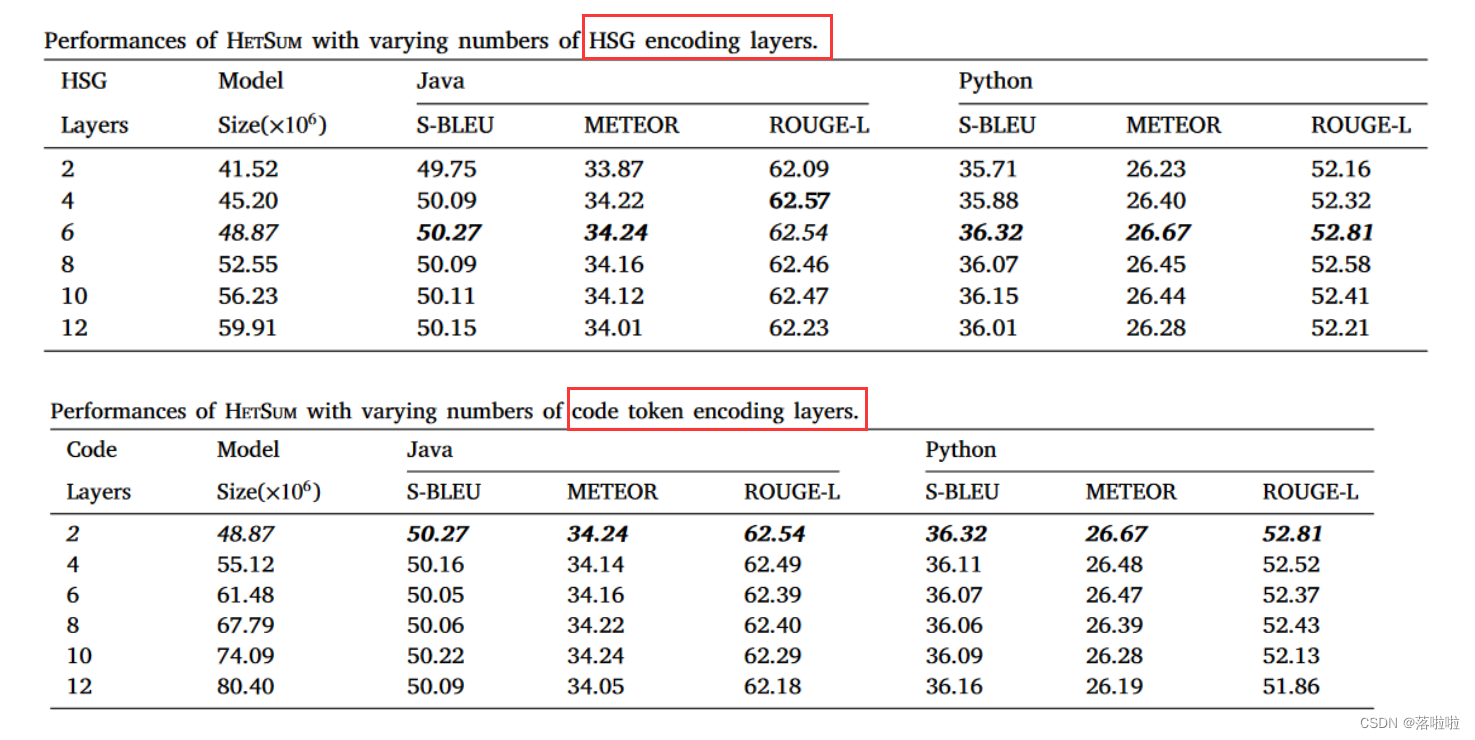
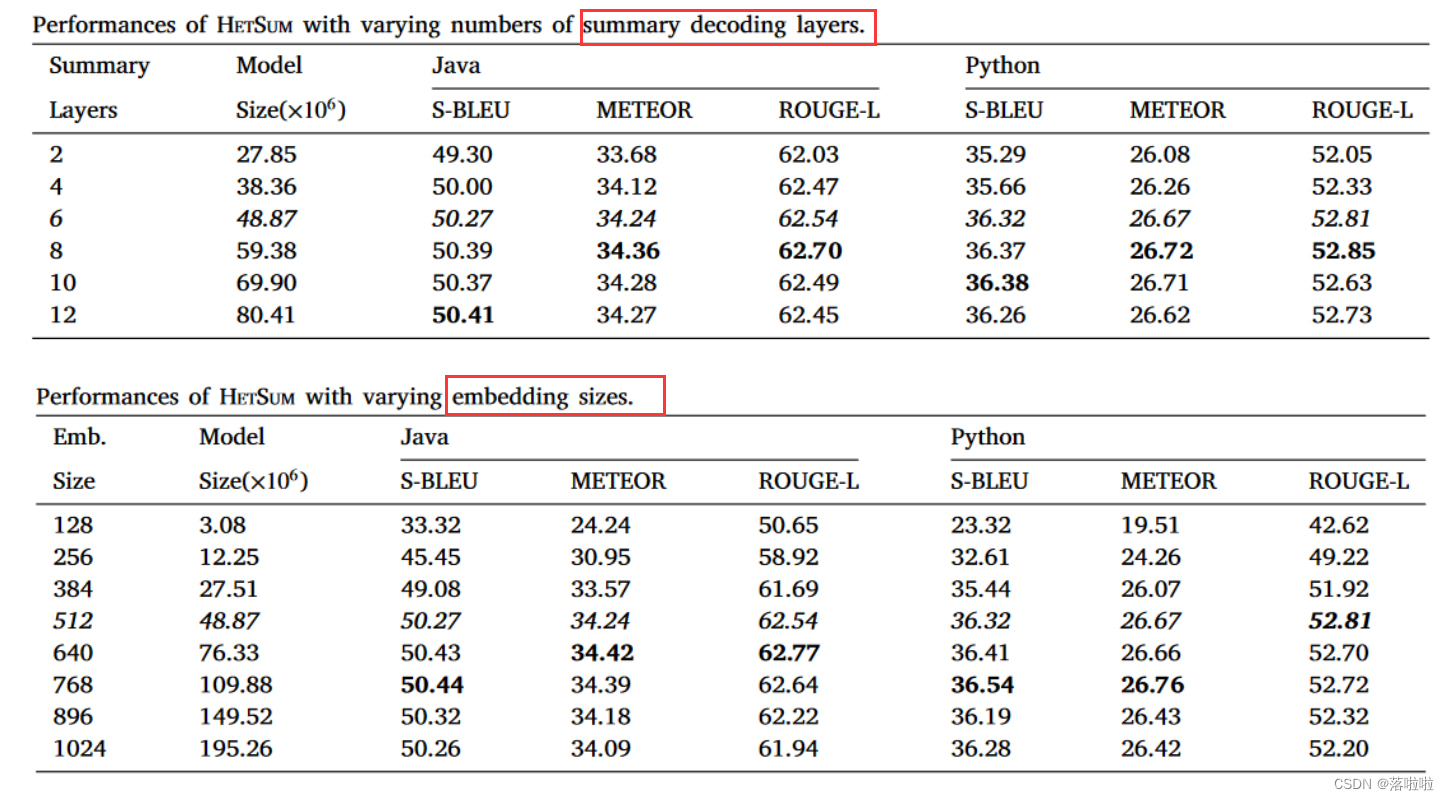
4.3 Model Size
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 黄金t+d与黄金期货交易的区别
- mysql学习打卡day4
- 新手能掌握 PyTorch 的填充技术:深入理解反射、复制、零值和常数填充
- 2024年天津农学院专升本专业课考试打印准考证等考场安排事宜通知
- 山海鲸可视化:开启生命科学探索新篇章
- 跬智信息(Kyligence)与光环云(Sinnet Cloud)达成战略合作
- TSINGSEE青犀智能分析网关V4智慧工地解决方案
- 《论文阅读28》Unsupervised 3D Shape Completion through GAN Inversion
- PPT插件-大珩助手-修改素材名称及搜索功能演示
- eslint严格规则检测问题报错