018文章解读与程序——中国电机工程学报EI\CSCD\北大核心《微电网两阶段鲁棒优化经济调度方法》已提供下载资源

👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆下载资源链接👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆

摘要：针对微电网内可再生能源和负荷的不确定性，建立了 min-max-min 结构的两阶段鲁棒优化模型，可得到最恶劣场 景下运行成本最低的调度方案。模型中考虑了储能、需求侧 负荷及可控分布式电源等的运行约束和协调控制，并引入了 不确定性调节参数，可灵活调整调度方案的保守性。基于列 约束生成算法和强对偶理论，可将原问题分解为具有混合整 数线性特征的主问题和子问题进行交替求解，从而得到原问 题的最优解。最终通过仿真分析验证了所建模型和求解算法 的有效性，同时给出了分时电价机制下微电网对储能进行调 度的边界条件，可为微电网投资商规划储能及配电网运营商 设计激励机制提供参考。

这段摘要描述了一项关于微电网优化的研究，以下是对摘要的详细解读：

1. 问题描述：

   • 研究的主要问题是微电网内可再生能源和负荷存在不确定性，因此建立了一种最小-最大-最小（min-max-min）结构的两阶段鲁棒优化模型。该模型的目标是找到在最恶劣情景下能够实现运行成本最低的调度方案。

2. 模型特点：

   • 模型考虑了储能、需求侧负荷以及可控分布式电源等的运行约束和协调控制。为了增强模型的鲁棒性，引入了不确定性调节参数，使得可以在调整调度方案的保守性方面具有灵活性。

3. 求解方法：

   • 采用了列约束生成算法和强对偶理论，将原始问题分解为具有混合整数线性特征的主问题和子问题，通过交替求解得到原问题的最优解。这种方法有助于有效地处理模型中的复杂约束和变量。

4. 验证和仿真分析：

   • 通过仿真分析验证了建立的模型和采用的求解算法的有效性。这表明所提出的方法在处理微电网优化问题时能够得到可行的解决方案。

5. 边界条件和应用：

   • 提供了分时电价机制下微电网对储能进行调度的边界条件。这对微电网投资商规划储能以及配电网运营商设计激励机制提供了参考，强调了该研究在实际应用中的潜在价值。

总体而言，这项研究通过建立鲁棒优化模型和采用有效的求解算法，针对微电网的不确定性问题提出了可行的解决方案，并在仿真中验证了其有效性和实用性。提供的边界条件和应用建议为微电网系统的规划和运营提供了有益的信息。

部分代码展示：

function [x, LB, y] = MP(u)
%% 设参
pm_max=1500;%联络线功率上限
eta=0.95;%储能充放电效率
p_g_max=800;
p_g_min=80;
ps_max=500;
ES_max=1800;
ES_min=400;
ES0=1000;
DDR=2940;

DR_max=200;
DR_min=50;

a=0.67;
b=0;
KS=0.38;
KDR=0.32;
price = [0.48;0.48;0.48;0.48;0.48;0.48;0.48;0.9;1.35;1.35;1.35;0.9;0.9;0.9;0.9;0.9;0.9;0.9;1.35;1.35;1.35;1.35;1.35;0.48];
%这是个列向量

PW_=[0.6564    0.6399    0.6079    0.5594    0.5869    0.5794    0.6138    0.6192   0.6811    0.6400    0.7855    0.7615    0.6861    0.8780    0.6715    0.7023    0.6464    0.6321    0.6819    0.6943    0.7405    0.6727    0.6822    0.6878];
%p_pv=1500*[     0         0         0         0         0    0.0465    0.1466    0.3135     0.4756    0.5213    0.6563    1.0000    0.7422    0.6817    0.4972    0.4629    0.2808    0.0948    0.0109         0         0         0         0         0];
%PL=1500*[ 0.4658    0.4601    0.5574    0.5325    0.5744    0.6061    0.6106    0.6636    0.7410    0.7080    0.7598    0.8766    0.7646    0.7511    0.6721    0.5869    0.6159    0.6378    0.6142    0.6752    0.6397    0.5974    0.5432    0.4803];
%这三个是横向量    

P_DR=1*[110 100 90 80 100 100 130 100 120 160 175 200 140 100 100 120 140 150 190 200 200 190 80 60];
%这是个行向量

%%设决策变量
p_ch=sdpvar(1,24,'full');%储能充电
p_dis=sdpvar(1,24,'full');%储能放电
us=binvar(1,24,'full');%充放电标识

p_buy=sdpvar(1,24,'full');%配网购电
p_sell=sdpvar(1,24,'full');%配网售电
um=binvar(1,24,'full');%购售电标识

%p_pv=sdpvar(1,24,'full');%光伏发电
%pL=sdpvar(1,24,'full');%固定日负荷


p_g=sdpvar(1,24,'full');%分布式电源

PDR=sdpvar(1,24,'full');%可转移负荷
PDR1=sdpvar(1,24,'full');%可转移负荷辅助变量
PDR2=sdpvar(1,24,'full');%可转移负荷辅助变量

afa=sdpvar(1,1,'full');


%% 构建矩阵
x=[us,um]';%第一阶段变量
y=[p_g,p_ch,p_dis,PDR,PDR1,PDR2,p_buy,p_sell]';%第二阶段变量
%u=[p_pv,PL]';%不确定量。这里为确定量为最恶劣场景（子问题的解）

Q01=[eye(24),zeros(24,24)];%us
Q02=[zeros(24,24),eye(24)];%um

Q1=[eye(24),zeros(24,168)];
Q2=[zeros(1,24),eta.*ones(1,24),-1/eta.*ones(1,24),zeros(1,120)];

Q31=[zeros(24,24),eye(24),zeros(24,144)];%p_ch9c 
Q32=[zeros(24,48),eye(24),zeros(24,120)];%p_dis

Q4=[zeros(24,24),eta.*tril(ones(24,24),0),-1/eta.*tril(ones(24,24),0),zeros(24,120)];
Q51=[zeros(24,144),eye(24),zeros(24,24)];%p_buy
Q52=[zeros(24,168),eye(24)];%p_sell

Q6=[eye(24),-eye(24),eye(24),-eye(24),zeros(24,24),zeros(24,24),eye(24),-eye(24)];

%Q7=[zeros(24,72),eye(24),-eye(24)];

Q8=[zeros(1,72),ones(1,24),zeros(1,96)];
Q9=[zeros(24,72),eye(24),zeros(24,96)];

Q101=[zeros(24,96),eye(24),zeros(24,72)];
Q102=[zeros(24,120),eye(24),zeros(24,48)];
Q103=[zeros(24,72),eye(24),eye(24),-eye(24),zeros(24,48)];
,
QCS=[zeros(24,24),KS*eta.*eye(24),KS*1/eta.*eye(24),zeros(24,120)];
QCDR=[zeros(24,96),KDR*eye(24),KDR*eye(24),zeros(24,48)];
QCM=[zeros(24,144),eye(24),-eye(24)];
QC=[a*ones(1,24),KS*eta.*ones(1,24),KS*1/eta.*ones(1,24),zeros(1,24),KDR*ones(1,24),KDR*ones(1,24),price'.*ones(1,24),-price'.*ones(1,24)];


G1=[eye(24),-eye(24)];

%T1=ps_max*[(1-us),us]';
%T2=pm_max*[(1-um),um]';


%% 增加原始约束
C=[-Q1*y>=-p_g_max];%分布式电源约束
C=C+[Q1*y>=p_g_min];

C=C+[-Q31*y-ps_max*Q01*x>=-ps_max];%储能约束
C=C+[-Q32*y>=-Q01*x*ps_max];
C=C+[Q31*y>=0];
C=C+[Q32*y>=0];
C=C+[Q2*y==0];%保证储能在调度前后能量相同
C=C+[-Q4*y>=-(ES_max-ES0)];
C=C+[Q4*y>=(ES_min-ES0)];

C=C+[-Q52*y-pm_max*Q02*x>=-pm_max];%配电网交互约束
C=C+[-Q51*y>=-Q02*x*pm_max];
C=C+[Q51*y>=0];
C=C+[Q52*y>=0];
C=C+[Q6*y+G1*u==0];

C=C+[Q8*y==DDR];%可转移负荷约束
C=C+[-Q9*y>=-DR_max];
C=C+[Q9*y>=DR_min];
C=C+[Q101*y>=0];
C=C+[Q102*y>=0];
%C=C+[Q9*y+Q101*y-Q102*y=P_DR];
C=C+[Q103*y==P_DR'];


%% 紧凑形式
%cy
%Dy>=d
%Ky=g
%Fx+Gy>=h
%Ly+Yu=0

D=[-Q1;Q1;Q31;Q32;-Q4;Q4;Q51;Q52;-Q9;Q9;Q101;Q102];
d=[-p_g_max*ones(24,1);p_g_min*ones(24,1);0*ones(24,1);0*ones(24,1);-(ES_max-ES0)*ones(24,1);(ES_min-ES0)*ones(24,1);0*ones(24,1);0*ones(24,1);-DR_max*ones(24,1);DR_min*ones(24,1);0*ones(24,1);0*ones(24,1)];

K=[Q2;Q8;Q103];
g=[0;DDR;P_DR'.*ones(24,1)];

效果展示：

018号资源-源程序：论文可在知网下载《微电网两阶段鲁棒优化经济调度方法》本人博客有解读资源-CSDN文库https://download.csdn.net/download/LIANG674027206/88705575

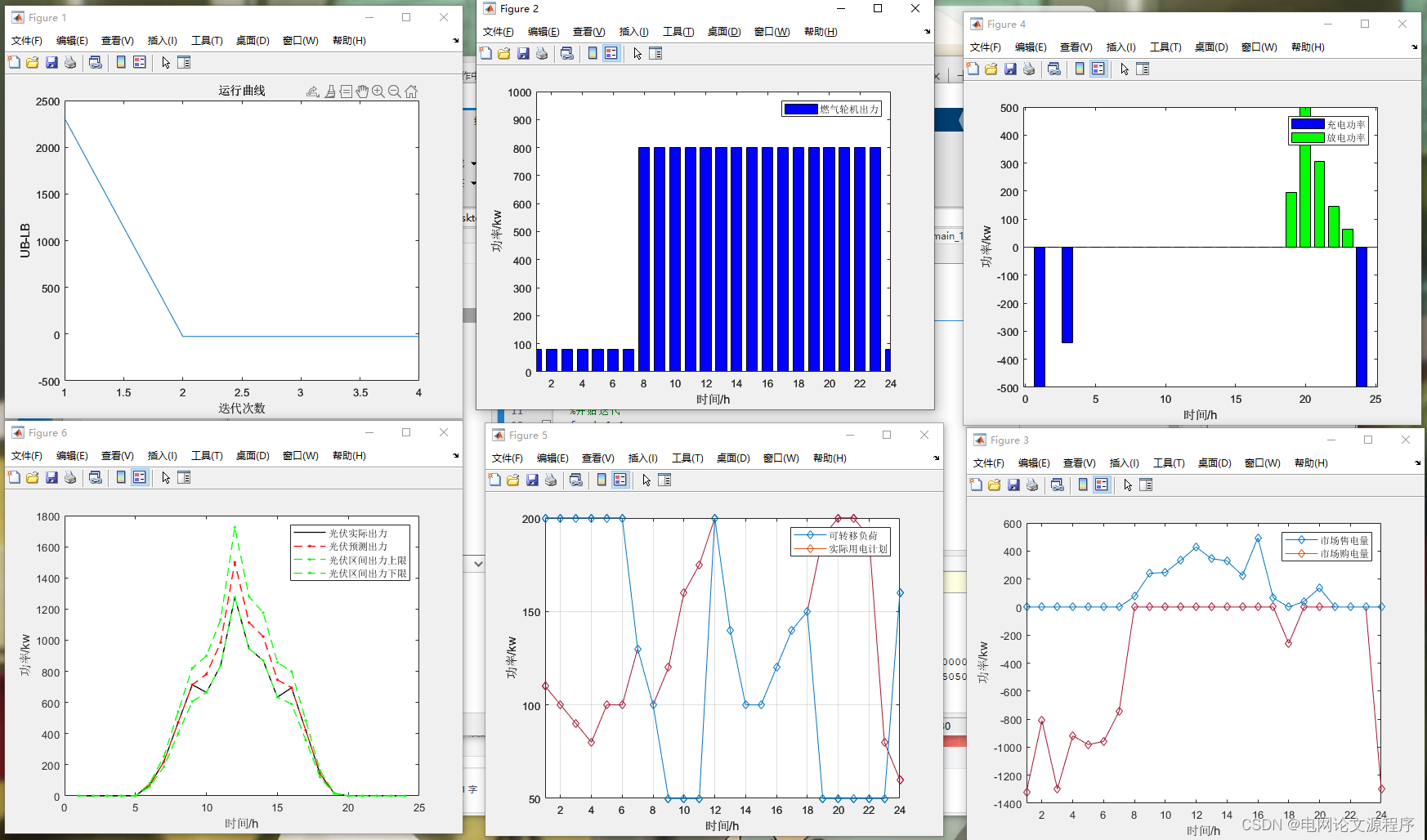
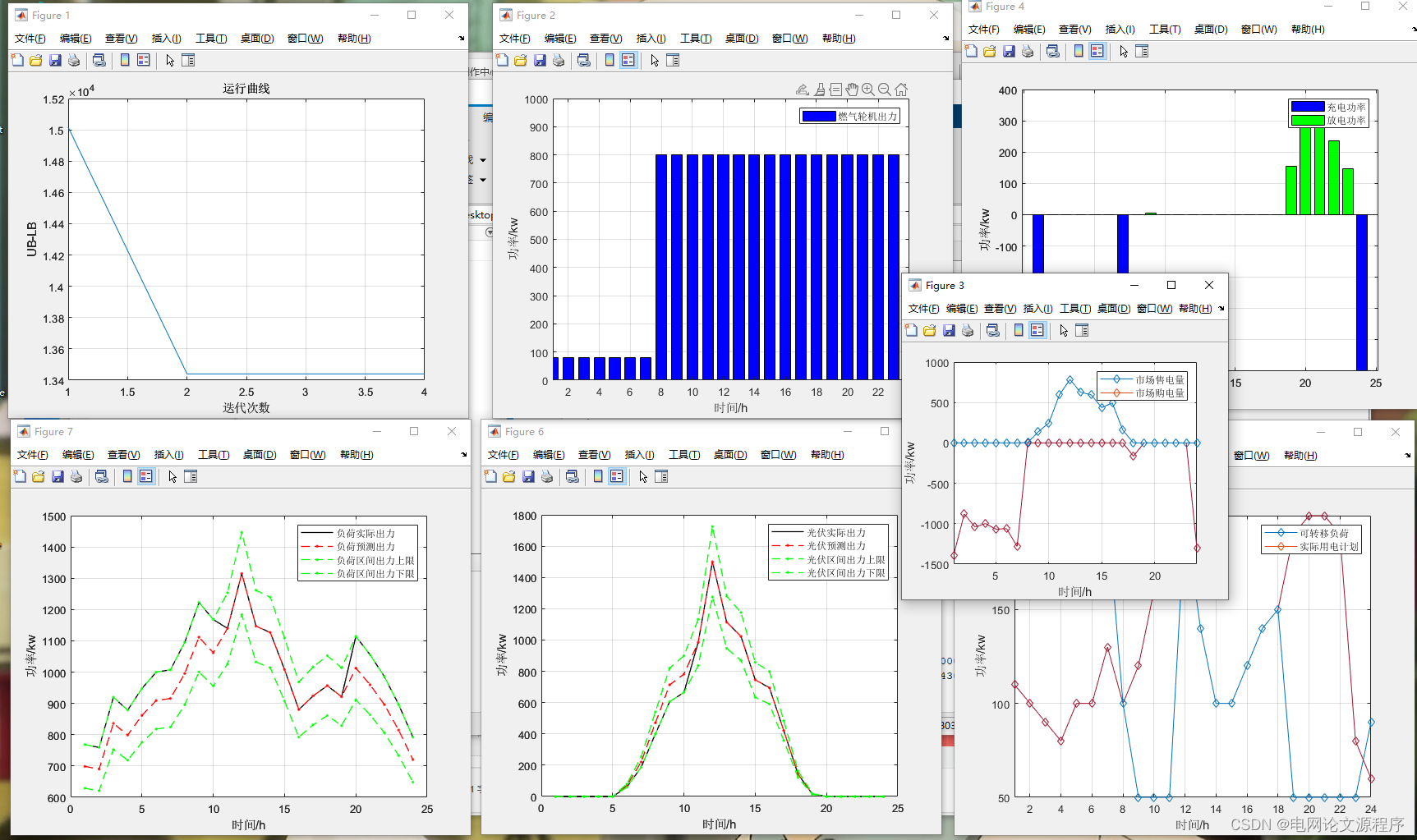
👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆下载资源链接👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆