正定矩阵的四个重要性质（附例子）

目录

一. 写在前面

二. 正定矩阵的基本定义

三. 从正定矩阵 到 特征值

四. 从特征值 到 正定矩阵

五. 从正定矩阵 到 行列式

六. 从正定矩阵 到 矩阵的主元

七. 从矩阵的主元 到 正定矩阵

八. 简单的讨论

8.1 行列式检验

8.2 特征值检验

总结

---

一. 写在前面

在格密码的安全性归约证明中，有时要求格基是正定矩阵，本文章梳理正定矩阵的四个性质，也可以将其作为正定矩阵的判定方法。

需要用到几个线性代数的基础结论：

1. 矩阵特征值的和等于对角线元素的和，求和的结果为矩阵的迹（trace）
2. 矩阵特征值的积等于矩阵的行列式；
3. 对称矩阵拥有标准正交的特征向量；
4. 矩阵的主元等于相邻子矩阵行列式的比值；

二. 正定矩阵的基本定义

正定矩阵的前提要求是对称矩阵，要求对任意非零向量，满足：

先看一个简单的2行2列矩阵：

正定矩阵在格密码中的应用（知识铺垫）-CSDN博客

这篇文章告诉我们，满足如下条件的矩阵A即可被称之为正定矩阵：

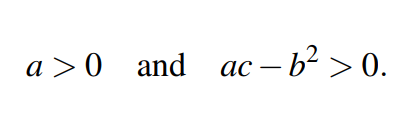
矩阵特征值的和等于对角线元素的和，也就是矩阵的迹，很明显：

矩阵特征值的积等于矩阵的行列式，2行2列的矩阵有2个特征值，所以可得：

综上可以初步感受到正定矩阵的特征值均为正数。

还有另外一个有用的参数，叫矩阵的主元（pivot）。如果将的结果表示成完全平方差的结果，既可以得到矩阵的主元，如下：

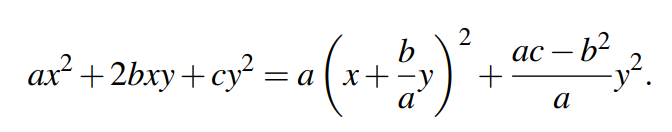
第一个完全平方式的系数为a，第二个完全平方式的系数为，这两个元素的值即为矩阵的主元。

备注：2行2列矩阵的主元有两个。

很明显函数系数均为正数，即主元均为正数的话，就可以直接判定矩阵的正定性。

三. 从正定矩阵 到 特征值

证明：正定矩阵的特征值均为正数。

设特征值为，特征向量为x，由此可得：

两边同时乘以向量x的转置，可得：

正定矩阵的定义告诉我们，左边为正数。所以，右边为正数，也就是所有特征值为正数。

证明完毕

四. 从特征值 到 正定矩阵

证明：矩阵的特征值均为正数时，该矩阵为正定矩阵。

也就是已知：

尝试证明：

注意此处的x要求对任意向量成立，而不仅仅是特征向量。

线性代数基础知识告诉我们，对称矩阵拥有标准正交的特征向量（orthonormal eigenvectors），将其表示为，所以给定任意向量x都可以表示成标准正交的特征向量，如下：

由此，将矩阵A与向量x的运算，改写为：

第一个等号：将向量x直接改写，并将常数c提到最前面；

第二个等号：特征值与特征向量的关系；简单复习下标准正交的性质。正交性告诉我们:

标准性（normalization）告诉我们：

由此将刚才的等式两边同时乘以向量x的转置，可得：

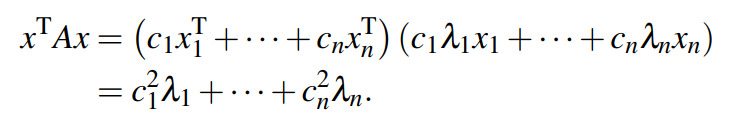
第一个等号：将向量x的转置表示成标准正交特征向量的格式；

第二个等号：正交性与标准性质；

当所有的特征值大于0，也就是时，可得左边也为正数，也就是。

证明完毕。

五. 从正定矩阵 到 行列式

先看一个简单例子：

很容易计算，该矩阵的行列式为1，detA=1。

但这个矩阵是负的单位阵：

很明显不是正定矩阵，更准确来讲是负定矩阵（negative definite）。这也说明单纯看行列式的正负是不能反应矩阵的正定性。

那怎么办？

对于n维的矩阵来讲，从左上角开始，它的子矩阵，并且要求是方阵的情况，一共有n种，如下：

证明：正定矩阵的子矩阵行列式均为正的。

解：

任意矩阵A的行列式即为特征值的乘积。已经证明了，正定矩阵的特征值均为正数，那么说明矩阵A的行列式也肯定为正数，但现在，它的子矩阵怎么证明呢？

给出任意n维向量，我们考虑前k项任意，但要求后n-k项为0，那么可得：

也就是：

那么我们可以运算得到:

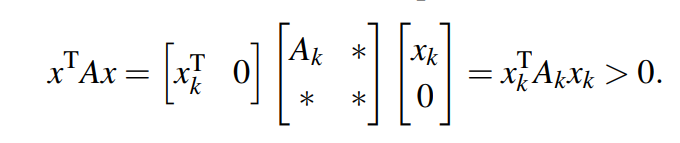
其中“*”代表原始矩阵A剩下的元素。

由此证明子矩阵也是正定的。该子矩阵的特征值也是正的，也就可以推出该子矩阵的行列式肯定为正数。

证明完毕。

六. 从正定矩阵 到 矩阵的主元

证明：正定矩阵的主元均为正数

解：

将矩阵的第k个主元叫，我们知道该值可以利用行列式求：

以上证明告诉我们，正定矩阵的行列式均为正数，子矩阵的行列式也为正数，所以可得矩阵的主元也为正数。

证明完毕。

七. 从矩阵的主元 到 正定矩阵

证明：当矩阵的主元均为正数时，该矩阵为正定矩阵。

解：

2行2列的矩阵肯定符合，这个我们在正定矩阵的定义中就证明过。

推广到任意n维矩阵时，需要将矩阵进行分解。分解成下三角矩阵和对称矩阵，如下：

接下来我们举个例子会更加清楚。

举一个三阶矩阵分解的例子，如下：

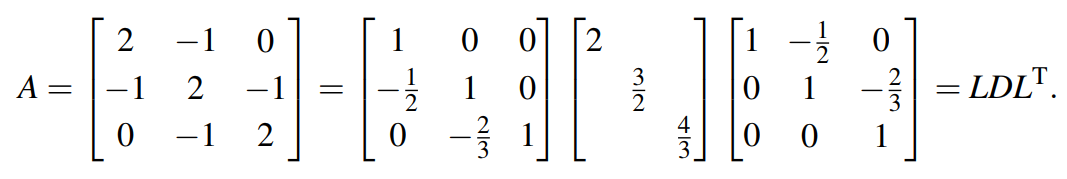
结合正定矩阵的要求，我们运算：

三阶矩阵的对称三维向量，可以先做下三角矩阵与向量的运算：

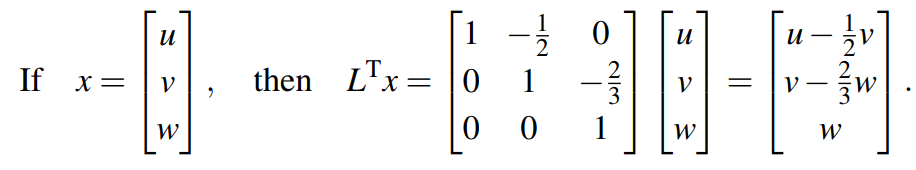
紧接着我们可以把矩阵与向量运算的结果表示成函数的格式。在写之前，我们就知道了矩阵的主元是位于完全平方差系数的位置，由此可得：

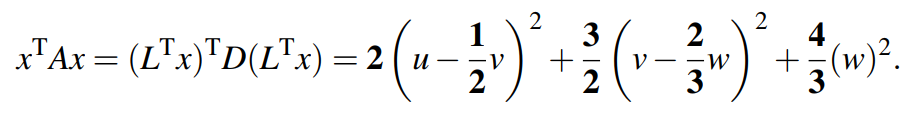
很显然当矩阵主元均为正数时，该函数也肯定恒为正数，也就是为正数，也就是A为正定矩阵。

证明完毕。

备注：特征值与矩阵的主元是两个完全不一样的元素。

八. 简单的讨论

还是以刚才三阶矩阵为例子。

8.1 行列式检验

我们可以首先用特征值对每个子矩阵进行判断下：

全为正数，再次说明A为正定矩阵。

8.2 特征值检验

三阶对称矩阵的特征值有三个数，可得：

全为正数，再次说明A为正定矩阵。

总结

正定矩阵拥有如下性质：

• 正定矩阵的特征值均为正数。
• 正定矩阵的子矩阵行列式均为正的。
• 正定矩阵的主元均为正数
• 正定矩阵对任意向量x，满足

以上均为充分必要条件，也就是可以将这四个作为正定矩阵的判定条件，也是可以的。在格密码利用矩阵进行安全性分析时，以上性质会非常有用，比如格基矩阵怎么取等等。