LORA的基本原理

本文将介绍如下内容：

• 什么是Lora
• 高效微调的基本原理
• LORA的实现方式
• LORA为何有效？

一、什么是LoRA

LoRA 通常是指低秩分解（Low-Rank Decomposition）算法，是一种低资源微调大模型方法，论文如下: LoRA: Low-Rank Adaptation of Large Language Models。
使用LORA，训练参数仅为整体参数的万分之一、GPU显存使用量减少2/3且不会引入额外的推理耗时。

二、高效微调的基本原理

以语言模型为例，在微调过程中模型加载预训练参数 ${\Phi }_0$进行初始化,并通过最大化条件语言模型概率进行参数更新 ${\Phi }_0$+$\Delta \Phi$，即：

这种微调方式主要的缺点是我们学习到的参数增量$\Delta \Phi$的维度和预训练参数${\Phi }_0$是一致的，这种微调方式所需的资源很多，一般被称为full fine-tuing。
研究者认为能用更少的参数表示上述要学习的参数增量$\Delta \Phi$=$\Delta \Phi (\Theta )$，其中$|\Theta |$<<$|{\Phi }_0|$，原先寻找$\Delta \Phi$的优化目标变为寻找$\Theta$：

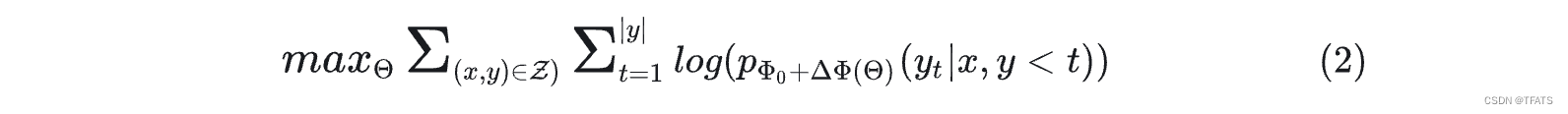
这种仅微调一部分参数的方法称为高效微调。针对高效微调，研究者有很多的实现方式(如Adapter、prefixtuing等)。本文作者旨在使用一个低秩矩阵来编码$\Delta \Phi$，相比于其他方法，LORA不会增加推理耗时且更便于优化。

三、LORA的实现方式

1、Instrisic Dimension

我们先思考两个问题：为何用数千的样本就能将一个数十亿参数的模型微调得比较好？为何大模型表现出很好的few-shot能力？
Aghajanyan的研究表明：预训练模型拥有极小的内在维度(instrisic dimension)，即存在一个极低维度的参数，微调它和在全参数空间中微调能起到相同的效果。
同时Aghajanyan发现在预训练后，越大的模型有越小的内在维度，这也解释了为何大模型都拥有很好的few-shot能力。

2、LORA

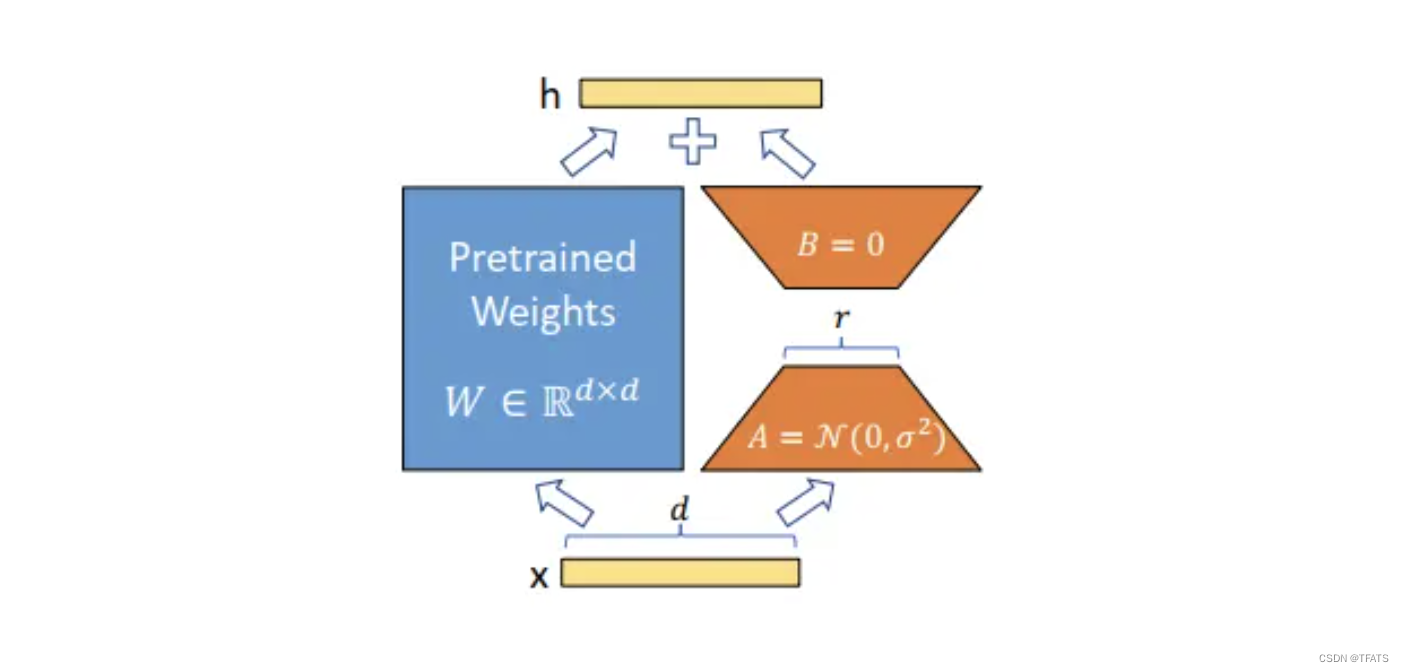
受instrisic dimension工作的启发，作者认为参数更新过程中也存在一个‘内在秩’。对于预训练权重矩阵$W_0$ $\in$ ${\mathbf{R}}^{\mathbf{d}?\mathbf{k}}$，我们可以用一个低秩分解来表示参数更新
$\Delta W$，即：

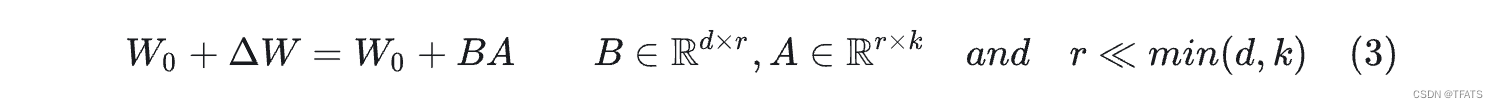
训练过程中冻结参数$W_0$，仅训练A和B中的参数。如上图所示，对于$h=W_{0}x$，前向传播过程变为：

四、LORA为何有效？

通过大量的对比实验，作者证明了LORA的有效性，但是作者希望进一步解释这种从下游任务中学到的低秩适应(low-rank adaptation)的特性。为此，作者提出了三个问题：

1、LORA应该作用于Transformer的哪个参数矩阵？

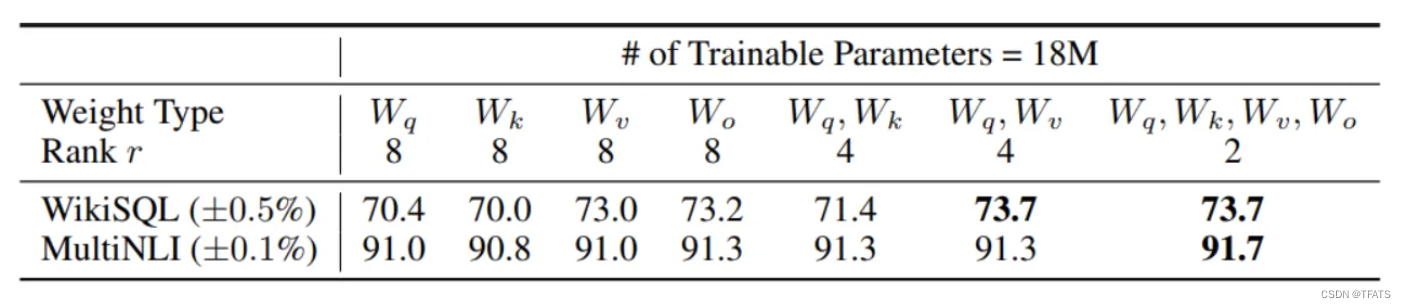
从上图我们可以看到：

• 将所有微调参数都放到attention的某一个参数矩阵的效果并不好，将可微调参数平均分配到$W_q$和$W_k$的效果最好。
• 即使是秩仅取4也能在$\Delta W$中获得足够的信息。

因此在实际操作中，应当将可微调参数分配到多种类型权重矩阵中，而不应该用更大的秩单独微调某种类型的权重矩阵。

2、LORA最优的秩r是多少？

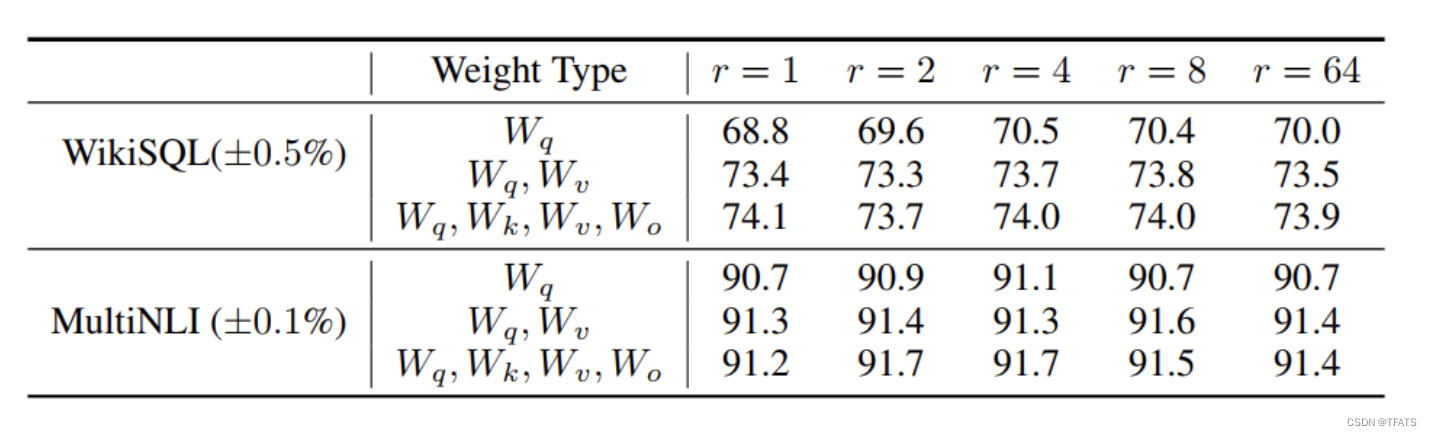
从上述实验结论我可以看到，在秩小到1或者2的时候，LORA的仍有不错的效果。因此作者假设:更新参数矩阵$\Delta W$可能拥有极小的‘内在秩’。为求证此假设，作者需要计算不同秩对应的子空间之间的重叠程度，如下：
对于 $r=8$ 和 $r=64$ 两个秩，首先进行奇异值分解得到两个右奇异矩阵$U_{Ar=8}$和$U_{Ar=64}$。作者希望得到：$U_{Ar=8}$ 的top-i奇异向量有多少被包含在$U_{Ar=64}$的top-j个向量中。可用格拉斯曼距离来表示这种子空间之间的相似关系：


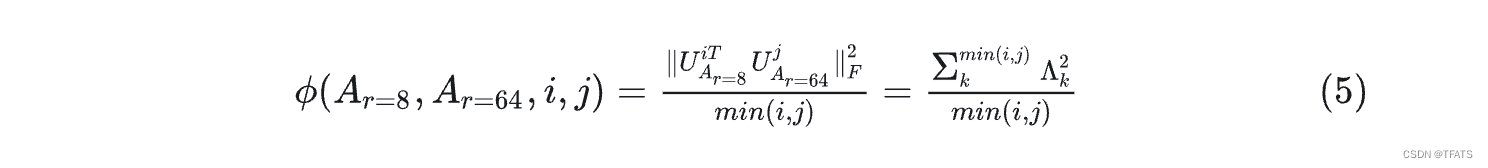
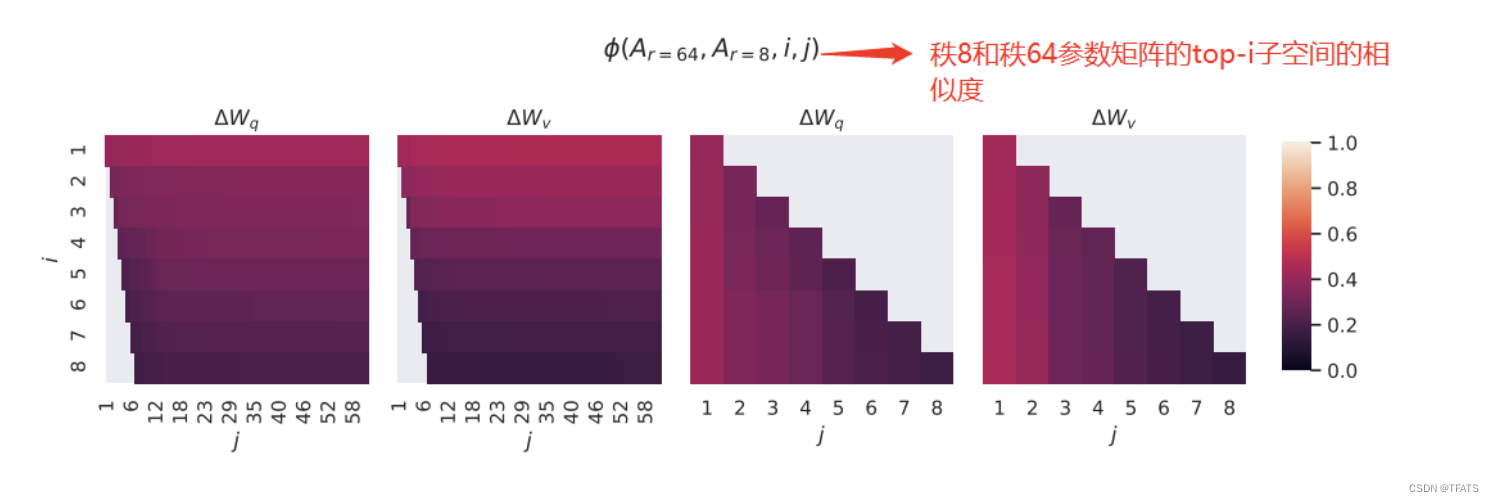
从上图可以看出$r=8$和$r=64$中的top奇异向量重叠得最多(颜色越小表示相似程度越高)，也就是说top奇异向量的作用最大，其他的奇异可能会引入更多的噪声。这证明了更新参数矩阵
$\Delta W$存在极小的‘内在秩’。

3、参数增量$\Delta W$和$W$的关系？

为揭示微调过程的内在原理，作者进行了如下实验：

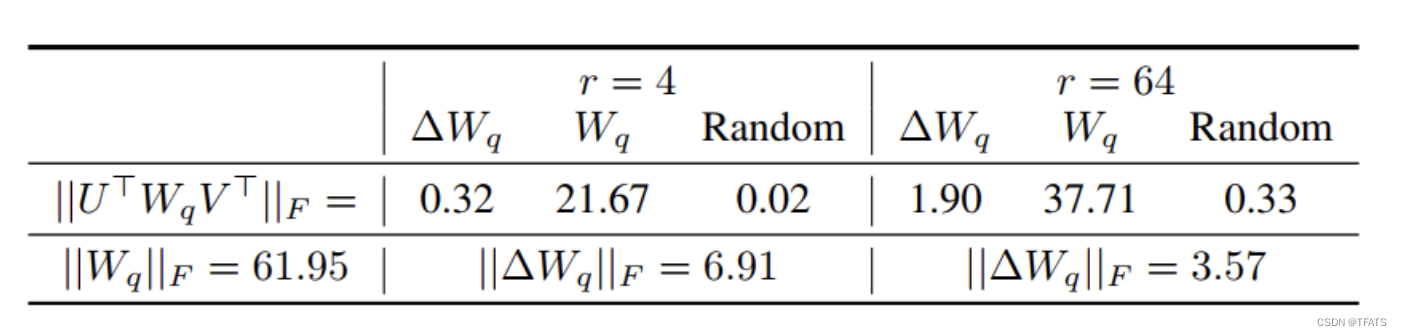
从上图的对比结果，作者发现三个现象：

• 相比于随机矩阵，$\Delta W$和 $W$有强关联。 从表中的$0.32>>0.02$可以看出。
• $\Delta W$仅放大了$W$中任务相关的特征， 并未放大头部特征。我们知道F范数的平方等于奇异值和的平方，因此从表中的$0.32<<21.67$可以看出$\Delta W$和$W$的头部奇异向量并无关联。
• r等于4时，$\Delta W$的放大系数已经很大了。 计算$6.91/0.32\approx 21.5$可知$\Delta W$能将 $W$ 中相关的特征向量放大21.5倍。

因此我们可以得到结论：在训练过程中，低秩的适应矩阵$\Delta W$仅仅放大了对下游任务有用的特征，而不是预训练模型中的主要特征。

参考：

• LORA微调系列(一)：LORA和它的基本原理