【滑动窗口精选题目】详解8道题

讲解【滑动窗口系列】的8道经典练习题，在讲解题目的同时给出AC代码??【注：点击题目即可打开链接】

注：滑动窗口最重要的是想到为什么要用【满足双指针同向】，而怎么用是次要的

目录

1、长度最小的子数组

2、无重复字符的最长子串

3、最大连续1的个数 III

4、将 x 减到 0 的最小操作数

5、水果成篮

6、找到字符串中所有字母异位词

7、串联所有单词的子串

8、?最小覆盖子串

---

1、长度最小的子数组

?解法一、暴力求解（会超时）：

「从前往后」枚举数组中的任意一个元素，把它当成起始位置。然后从这个「起始位置」开始，然后寻找一段最短的区间，使得这段区间的和「大于等于」目标值。将所有元素作为起始位置所得的结果中，找到「最小值」即可。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int ret = INT_MAX;
        int n = nums.size();

        //枚举出所有>=target的子数组[start,end]，并取最小值
        //枚举开始位置
        for (int start = 0; start < n; start++)
        {
            int sum = 0;
            //寻找结束位置
            for (int end = start; end < n; end++)
            {
                sum += nums[end];//加上当前位置的值

                if (sum >= target)
                {
                    ret = min(ret, end - start + 1);
                    break;//因为此时以start为开头的区间内连续子数组长度最小值已找到
                }
            }
        }
        //如果没有答案则返回0
        return ret == INT_MAX ? 0 : ret;
    }
};

解法二、滑动窗口 （概念引入+思路）

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int n = nums.size(), ret = INT_MAX, sum = 0;
        for (int left = 0, right = 0; right < n; right++)
        {
            sum += nums[right];//入窗口
            while (sum >= target)
            {
                ret = min(ret, right - left + 1);//取每次符合条件下的最小长度
                sum -= nums[left++]; //出窗口
            }
        }
        return ret == INT_MAX ? 0 : ret; 
    }
};

---

2、无重复字符的最长子串

解法一、暴力求解+哈希表（不会超时，可以通过）：

枚举「从每一个位置」开始往后，无重复字符的子串可以到达什么位置。找出其中?度最大的即可。在往后寻找无重复子串能到达的位置时，可以利用「哈希表」统计出字符出现的频次，来判断什么时候子串出现了重复元素。

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int ret = 0;//记录结果
        int n = s.size();

        //枚举起始位置
        for (int i = 0; i < n; i++)
        {
            //创建哈希表，统计出现频率
            //用数组就可以是因为本题只有字符
            int hash[128] = { 0 };
            //寻找终止位置
            for (int j = i; j < n; j++)
            {
                hash[s[j]]++; //出现字符的频次++
                if (hash[s[j]] > 1) break;//出现重复字符，则不符合要求
                ret = max(ret, j - i + 1);
            }
        }
        return ret;
    }
};

?解法二、滑动窗口+哈希

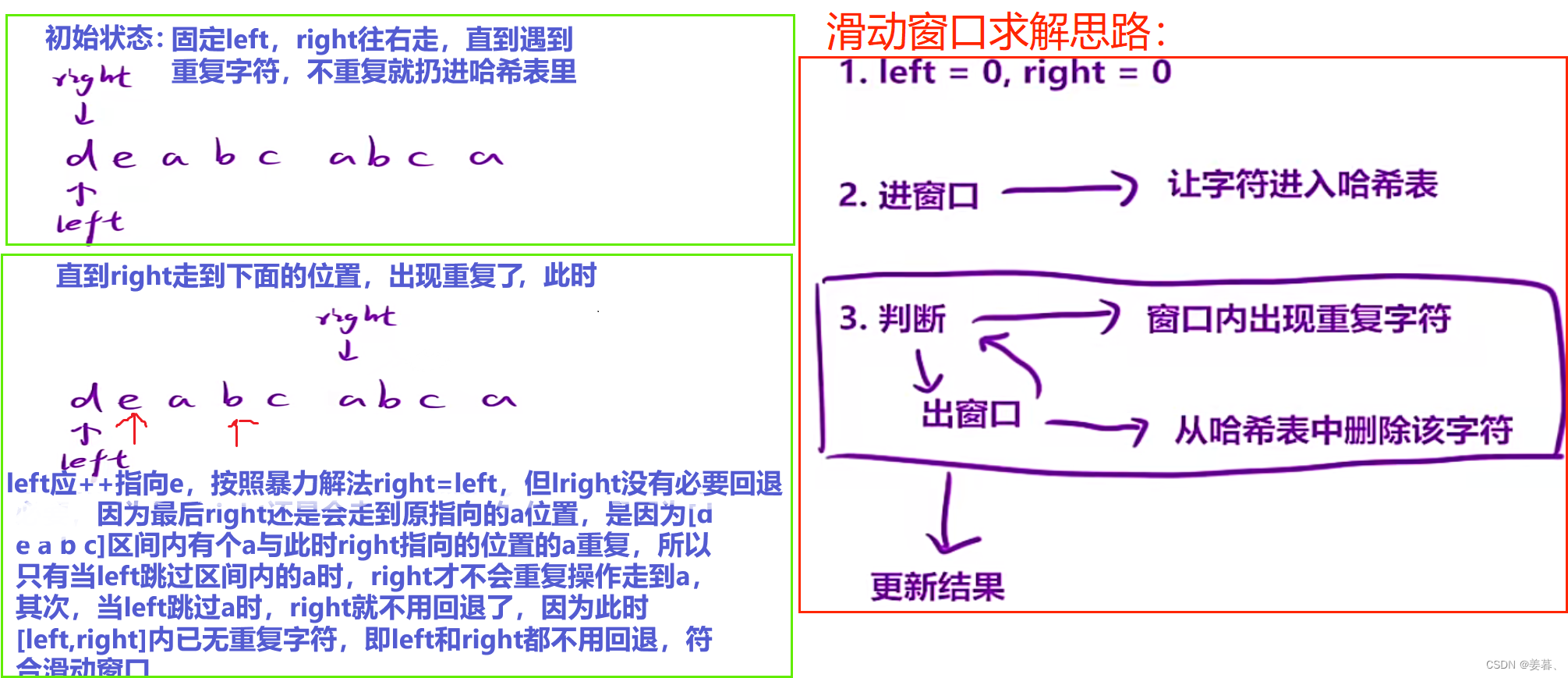
研究的对象依旧是一段连续的区间，因此继续使用「滑动窗口」思想来优化。
让滑动窗口满足：窗口内所有元素都是不重复的。
做法：右端元素?ch 进入窗口的时候，哈希表统计这个字符的频次：

• 如果这个字符出现的频次超过?1 ，说明窗口内有重复元素，那么就从左侧开始划出窗口，直到?ch 这个元素的频次变为?1 ，然后再更新结果。
• 如果没有超过?1 ，说明当前窗口没有重复元素，可以直接更新结果?

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int hash[128] = {0};//哈希表记录字符出现频次
        int left = 0, right = 0, n = s.size();
        int ret = 0;
        while (right < n)
        {
            hash[s[right]]++;//入窗口
            while (hash[s[right]] > 1)//判断
                hash[s[left++]]--;//出窗口，直到窗口内无重复元素
            ret = max(ret, right - left + 1);//更新结果
            right++;//让下一元素进入窗口
        }
        return ret;
    }
};

---

3、最大连续1的个数 III

?解法一、暴力枚举（超时）

class Solution {
public:
    int longestOnes(vector<int>& nums, int k) {
        int zero = 0;//计数器，统计子数组内0的个数
        int n = nums.size();
        int ret = 0, len = 0;
        for (int i = 0; i < n; i++)
        {//先固定i
            zero = 0;
            len = 0;
            for (int j = i; j < n; j++)
            {
                if (nums[j] == 0) zero++;
                if (zero > k) break;
                len++;
            }
            ret = max(ret, len);
        }
        return ret;
    }
};

至于为什么每次都先暴力枚举求解，是因为它是推出更优解法的前提

解法二、滑动窗口

class Solution {
public:
    int longestOnes(vector<int>& nums, int k) {
        int ret = 0;
        for (int left = 0, right = 0, zero = 0; right < nums.size(); right++)
        {
            if (nums[right] == 0) zero++;//入窗口
            while (zero > k)
            {//不满足条件，出窗口
                if (nums[left++] == 0) zero--;
            }
            ret =  max(ret, right - left + 1);
        }
        return ret;
    }
};

---

4、将 x 减到 0 的最小操作数

?题目分析：

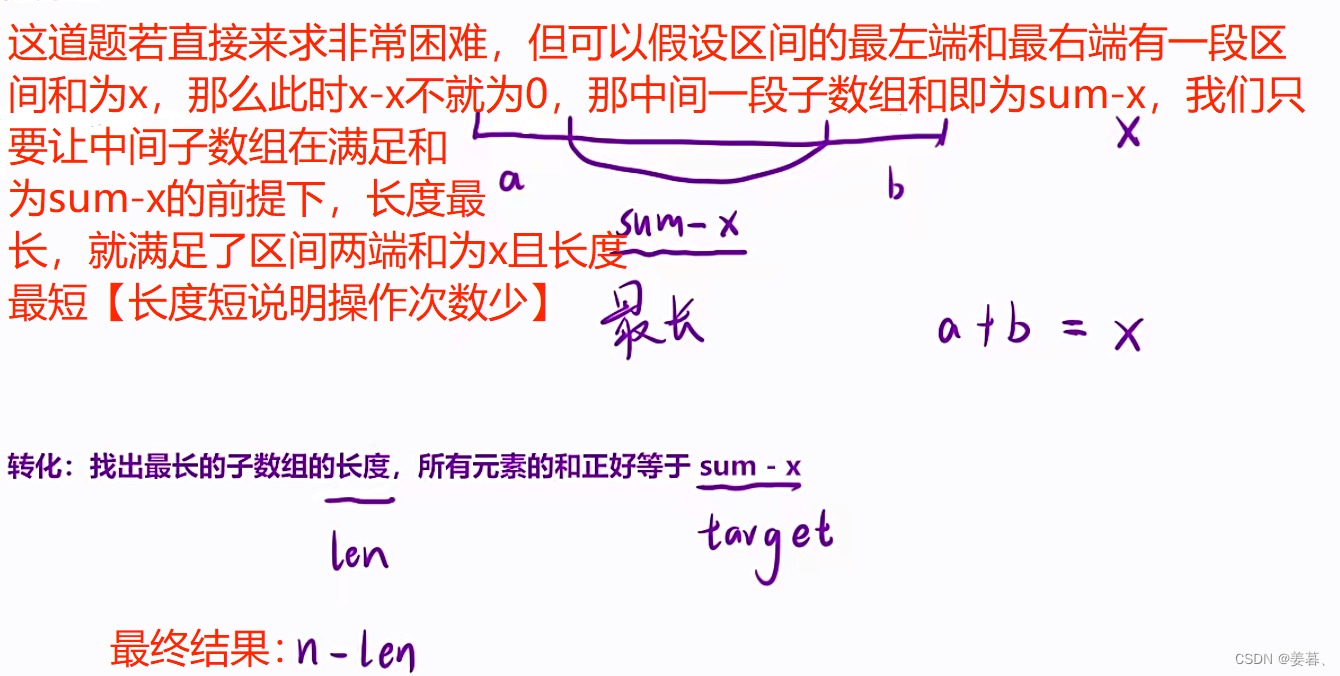
那么这个问题就转化为了本文讲的第一题的思路，再证明一下为什么要用滑动窗口?

class Solution {
public:
    int minOperations(vector<int>& nums, int x) {
        int sum = 0;
        for (auto e : nums) sum += e;
        int target = sum - x;
        if (target < 0) return -1;//所有和都比x小，则肯定不满足

        int ret = -1;
        for (int left = 0, right = 0, tmp = 0; right < nums.size(); right++)
        {
            tmp += nums[right];//进窗口
            while (tmp > target) tmp -= nums[left++];//出窗口
            if (tmp == target) ret = max(ret, right - left + 1);
        }   
        if (ret == -1) return -1;
        else return nums.size() - ret;//减掉最长的即最短的长度，即最少操作次数
    }
};

---

5、水果成篮

?题目分析：

最重要的是理解fruits数组中是这棵树含有的水果种类，而不是说种类有几种。比如示例2：[0,1,2,2]表示的是第一棵树上有0号水果，第二棵树上有1号水果，第三和第四棵树上有2号水果。

我们可以把问题转化为找出一个最长的子数组的长度，且子数组中不超过两种类型的水果

解法一、暴力枚举 + 哈希?

解法二、滑动窗口 + 哈希

下面是为什么要用滑动窗口的证明【重点】和如何使用滑动窗口 ：

①、 初始化哈希表hash来统计窗口内水果的种类和数量；
②、初始化变量：左右指针left=0，right=0，记录结果的变量ret=0；
③、当right小于数组大小的时候，一直执行下列循环：
i. 将当前水果放入哈希表中；
ii. 判断当前水果进来后，哈希表的大小：

• 如果超过2：
• 将左侧元素滑出窗口，并且在哈希表中将该元素的频次减一；
• 如果这个元素的频次减一之后变成了0，就把该元素从哈希表中删除；
• 重复上述两个过程，直到哈希表中的大小不超过2；

iii. 更新结果ret；
iv. right++，让下一个元素进入窗口；
④、 循环结束后，ret存的就是最终结果。

单单文字不好描述，最好是看看代码再理解理解，我会写出详细注释：

class Solution {
public:
    int totalFruit(vector<int>& f) {
        //如果觉得参数fruits太长，我们可以直接修改为f【不影响结果】

        //key值表示水果种类有几个，value值对应每个水果种类的数量
        unordered_map<int, int> hash;
        int ret = 0;
        for (int left = 0, right = 0; right < f.size(); right++)
        {
            //进窗口
            hash[f[right]]++;//这个种类水果的数量++
            //如果水果种类>2，则出窗口，是个持续过程
            while (hash.size() > 2)
            {
                hash[f[left]]--;
                //如果这个水果种类的数量为0，就要把它从哈希表中移除
                //本质是水果种类--，方便后续判断
                if (hash[f[left]] == 0) hash.erase(f[left]);
                left++;
            }
            ret = max(ret, right - left + 1);
        }
        return ret;
    }
};

因为题目中明确给了数据规模最大为100000，而哈希表的删除是影响效率的，删除的本质是去掉这个水果种类，所以可以优化一下，用一个变量kinds来直接求解

class Solution {
public:
    int totalFruit(vector<int>& f) {
        int hash[100010] = { 0 };

        int ret = 0;
        for (int left = 0, right = 0, kinds = 0; right < f.size(); right++)
        {
            if (hash[f[right]] == 0) kinds++;//如果进窗口前水果数量为0，则kinds++即可
            hash[f[right]]++;//进窗口
            //如果水果种类>2，则出窗口，是个持续过程
            while (kinds > 2)
            {
                hash[f[left]]--;//该种类的水果数量--
                if (hash[f[left]] == 0) kinds--;
                left++;
            }
            ret = max(ret, right - left + 1);
        }
        return ret;
    }
};

---

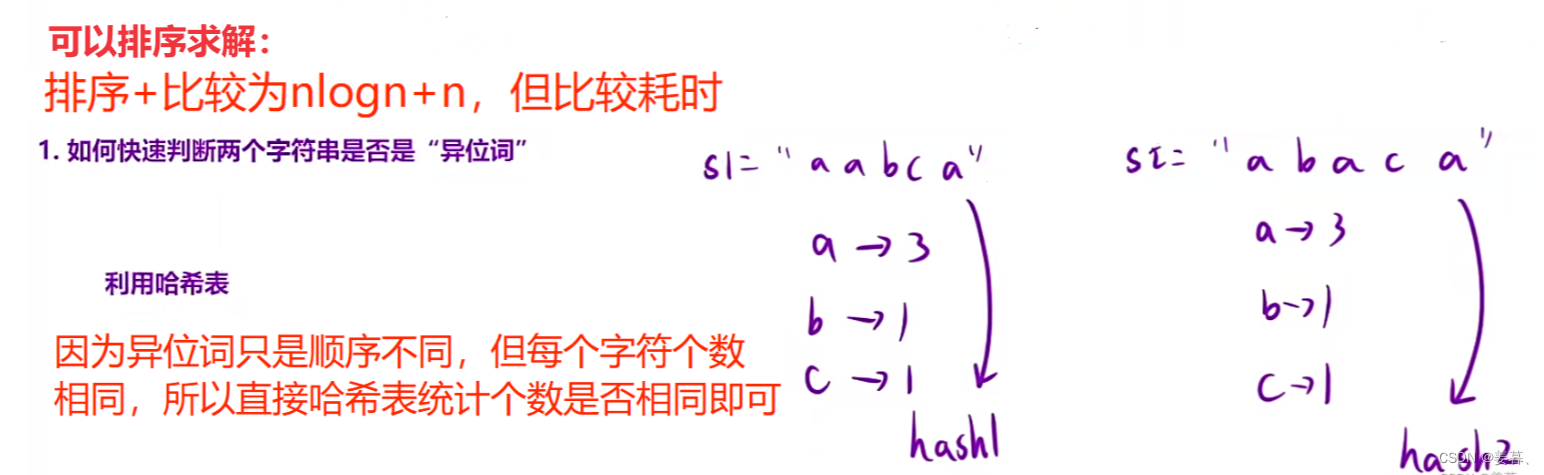
6、找到字符串中所有字母异位词

?

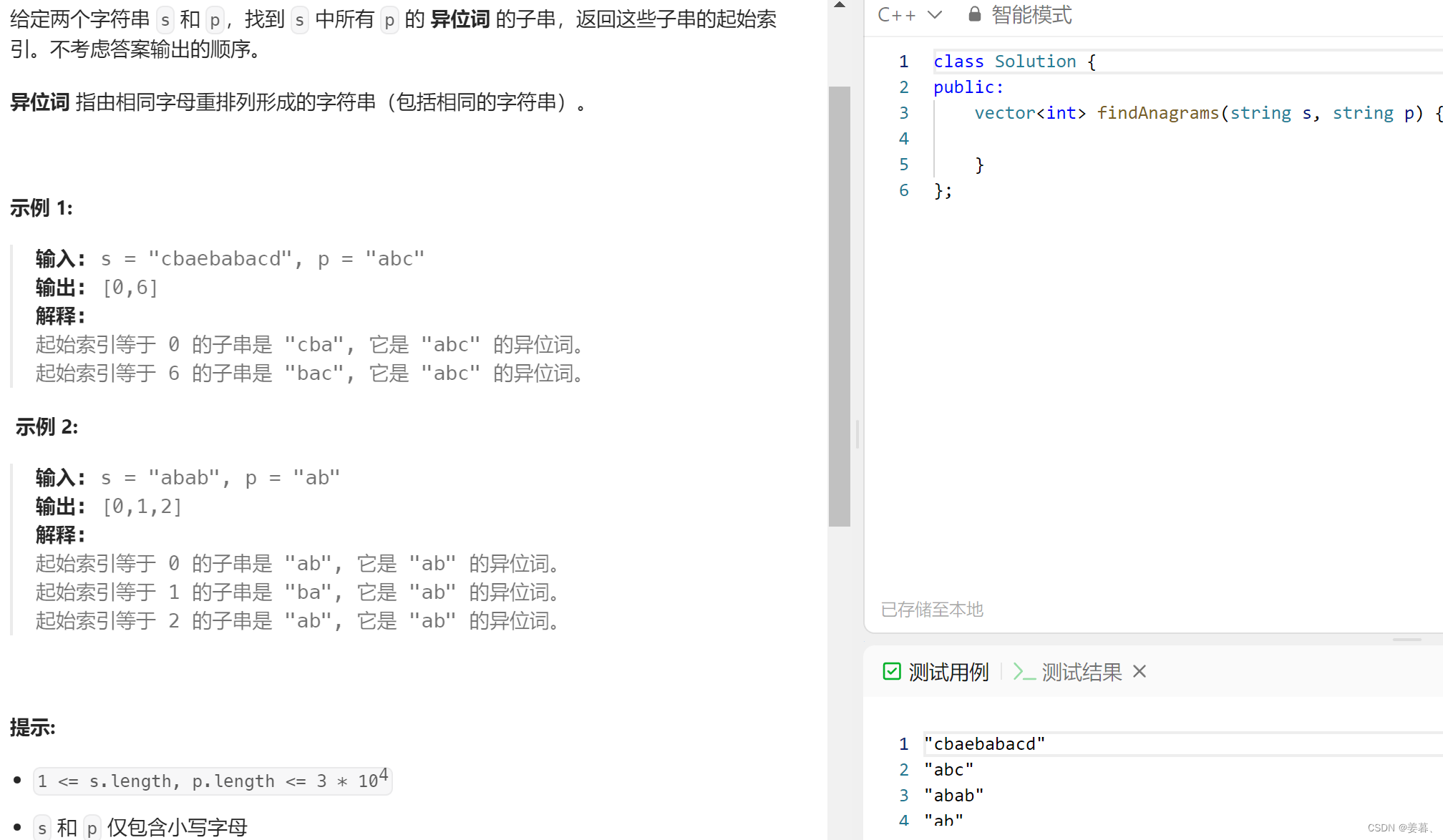解法一、暴力

解法二、滑动窗口?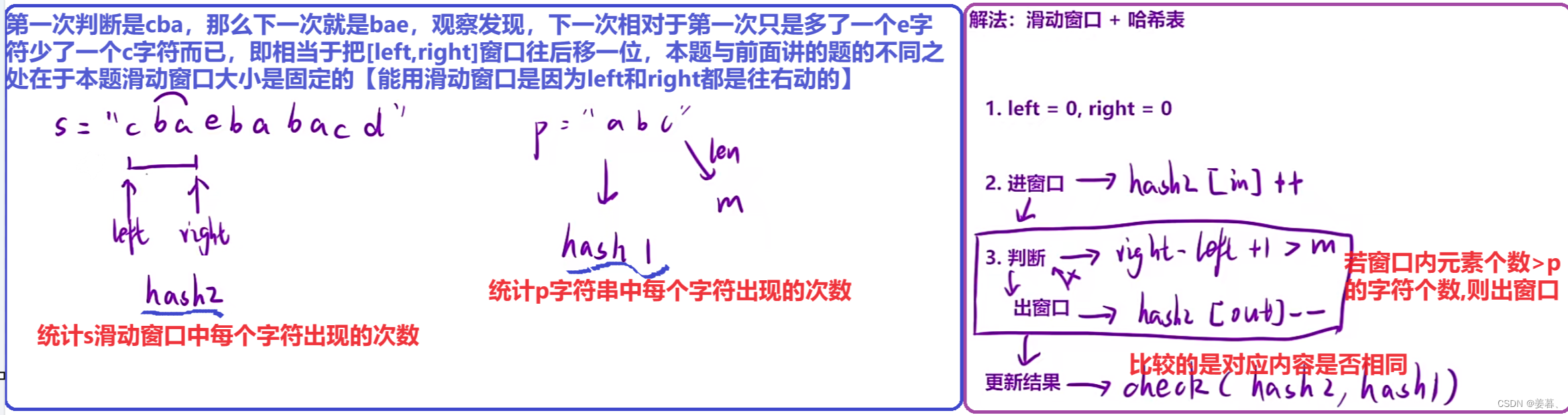

?上面解法的复杂度为26*N即O(N),上面解法因为都是字符，所以哈希表开个26空间的即可，但若每个元素都是个字符串呢【即等下讲的第7题】，就不具有通用性，所以接下来讲解一下通用解法

优化【重点】：

?

class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        vector<int> ret;
        int hash1[26] = {0};//统计p中每个字符出现的次数
        for (auto ch : p) hash1[ch - 'a']++;

        int hash2[26] = {0};//统计窗口中每个字符出现的次数
        int m = p.size();
        for (int left = 0, right = 0, count = 0; right < s.size(); right++)
        {
            char in = s[right];
            //判断s中right位置的字符进入窗口后，它的次数是否<=p中该字符的出现次数
            if (++hash2[in - 'a'] <= hash1[in - 'a']) count++;//进窗口+维护count
            //与之前的滑动窗口不同，这里判断一次即可，因为窗口每次就只会操作一个字符，
            //而之前讲的left可以移动好几次，所以是while，而这里if即可
            if (right - left + 1 > m)//若窗口内个数>p字符个数，则出窗口
            {
                char out = s[left++];//得到此字符后left一定会++
                //删除字符前判断是否要更新count
                if (hash2[out - 'a']-- <= hash1[out - 'a']) count--;
            }
            if (count == m) ret.push_back(left);//插入出现的其实下标
        }
        return ret;
    }
};

---

7、串联所有单词的子串

?

class Solution {
public:
    vector<int> findSubstring(string s, vector<string>& words) {
        vector<int> ret;//保存结果
        unordered_map<string, int> hash1;//统计每个字符串出现次数
        for (auto& s : words) hash1[s]++;

        int len = words[0].size(), m = words.size();
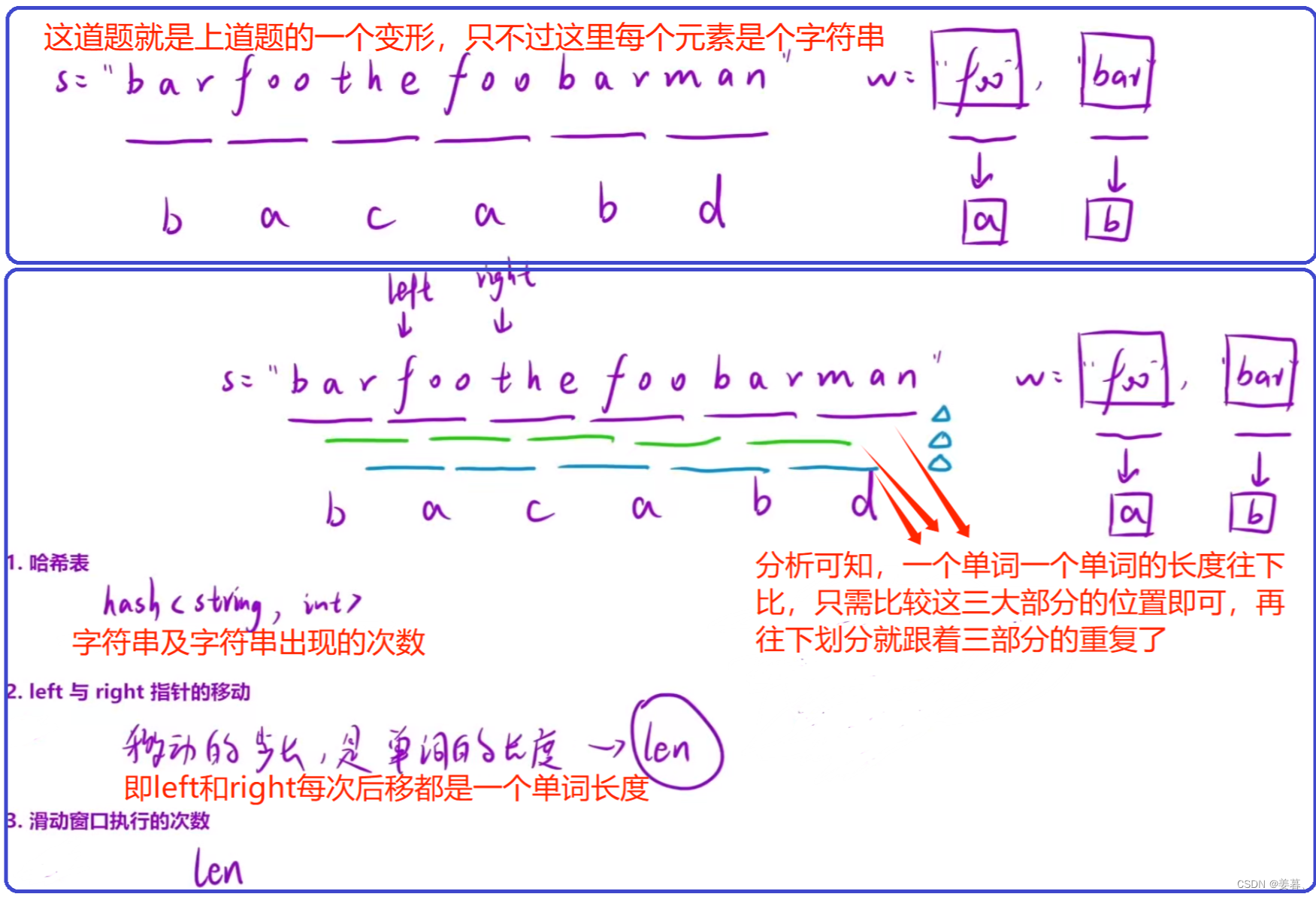
        for (int i = 0; i < len; i++)
        {//left和right起始位置[0,len-1]，并判断len次，由图分析出的
            //unordered_map一定每次循环定义一下，这样初始的size都为0，相当于重现开始
            unordered_map<string, int> hash2;//统计窗口内每个字符串出现次数
            for (int left = i, right = i, count = 0; right + len <= s.size(); right += len)
            {
                //进窗口+维护count
                string in = s.substr(right, len);//从当前right位置截取len长度的字符串
                hash2[in]++;//出现的字符串次数++
                //先判断hash1中有无in字符串，没有的话因为是unordered_map则会先插入字符串
                //会降低效率，所以这里优化下，先判断，即hash1.count(in)判断这个字符串在不在
                if (hash1.count(in) && hash2[in] <= hash1[in]) count++; 
                //出窗口
                if (right - left + 1 > len * m)//用right-left + len判断也行
                {
                    string out = s.substr(left, len);
                    //出窗口前先判断出现次数的关系以便维护count值
                    if (hash1.count(out) && hash2[out] <= hash1[out]) count--;
                    hash2[out]--;//出现次数--
                    left += len;
                }
                if (count == m) ret.push_back(left);
            }
        }
        return ret;
    }
};

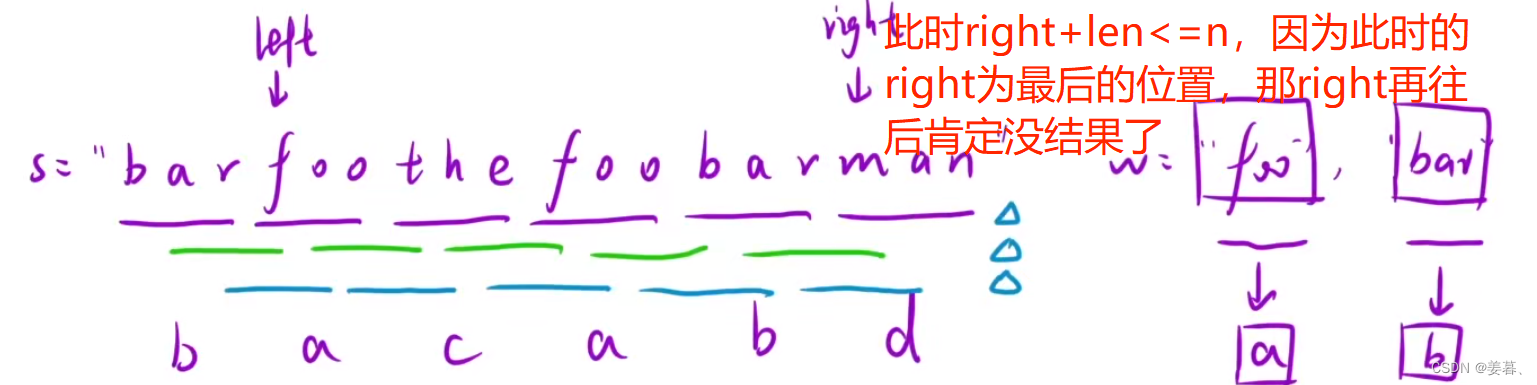
问题：为什么是right+len<=n作为循环条件？

---

8、?最小覆盖子串

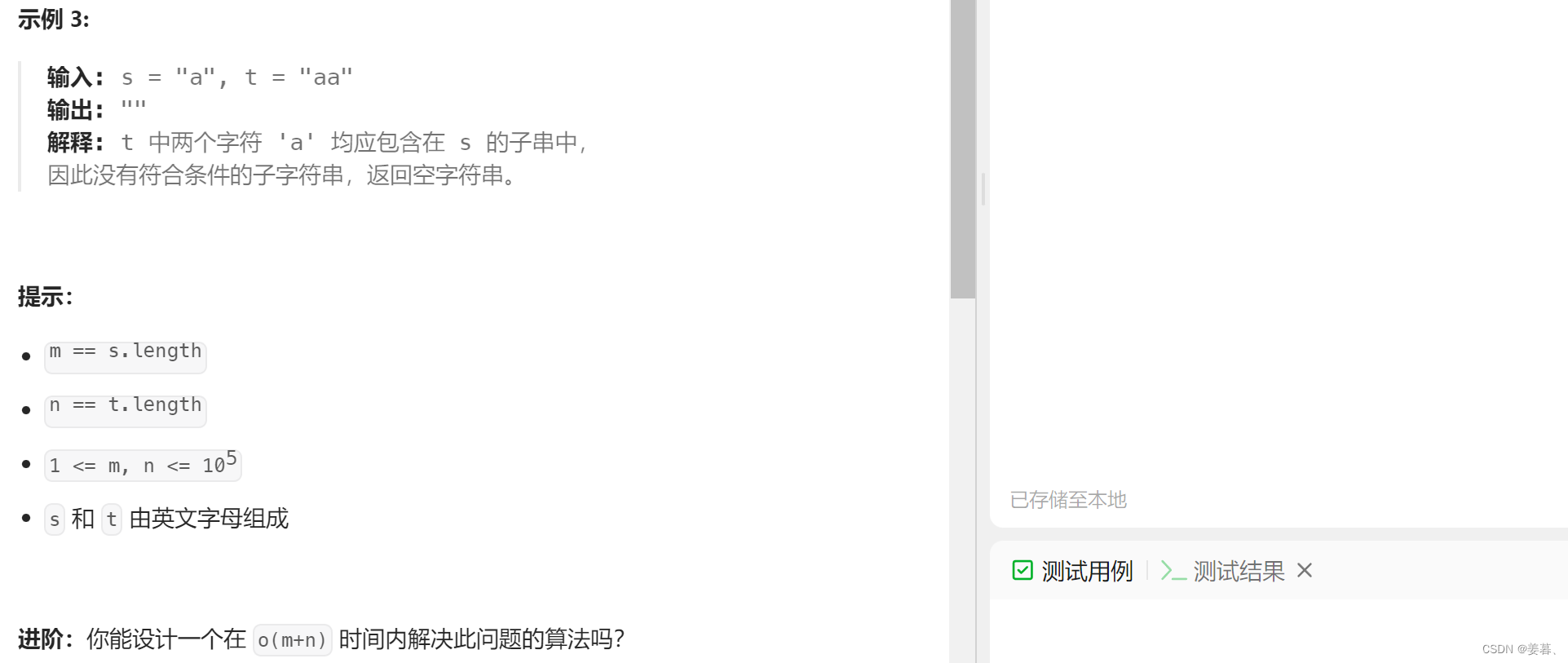
?解法一、暴力枚举+哈希表

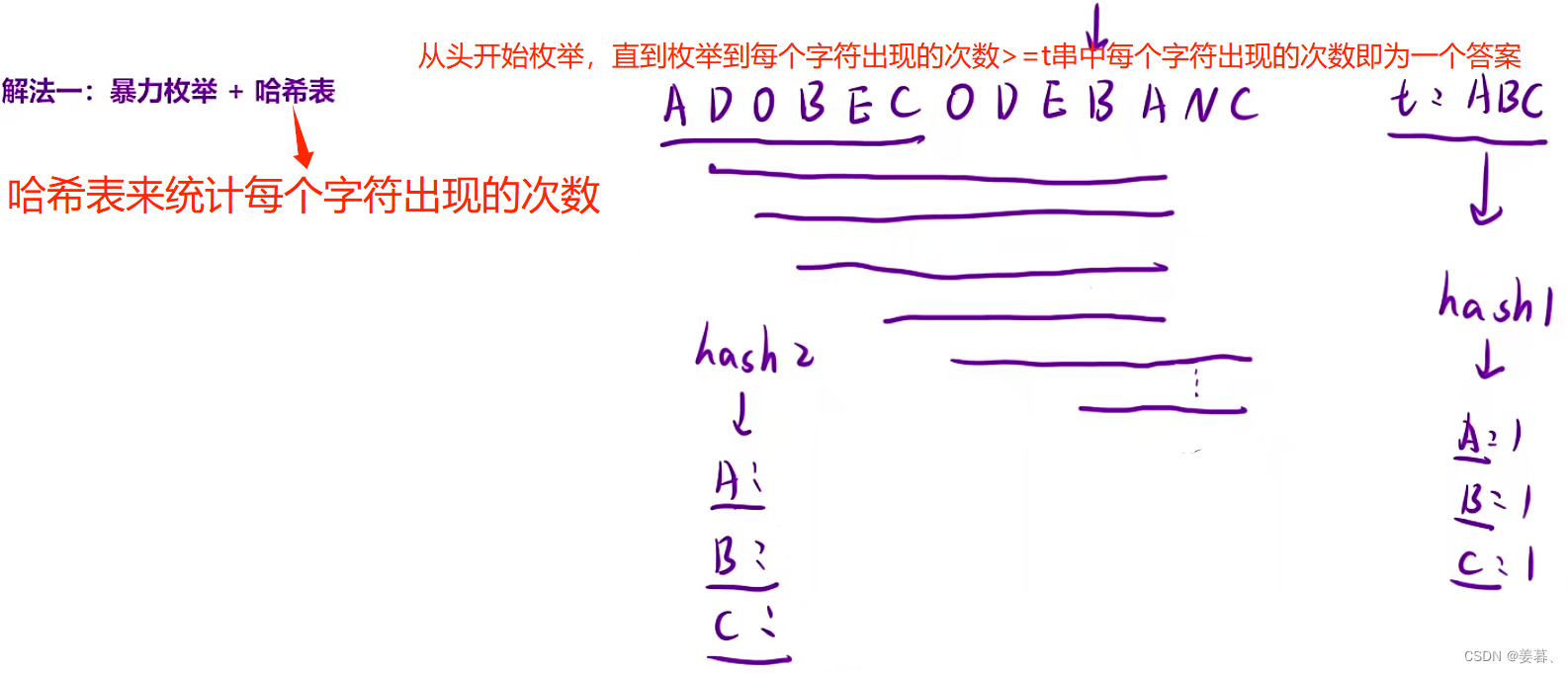
解法二、滑动窗口+哈希表

?为什么要使用滑动窗口？【更重要】

?怎么使用滑动窗口？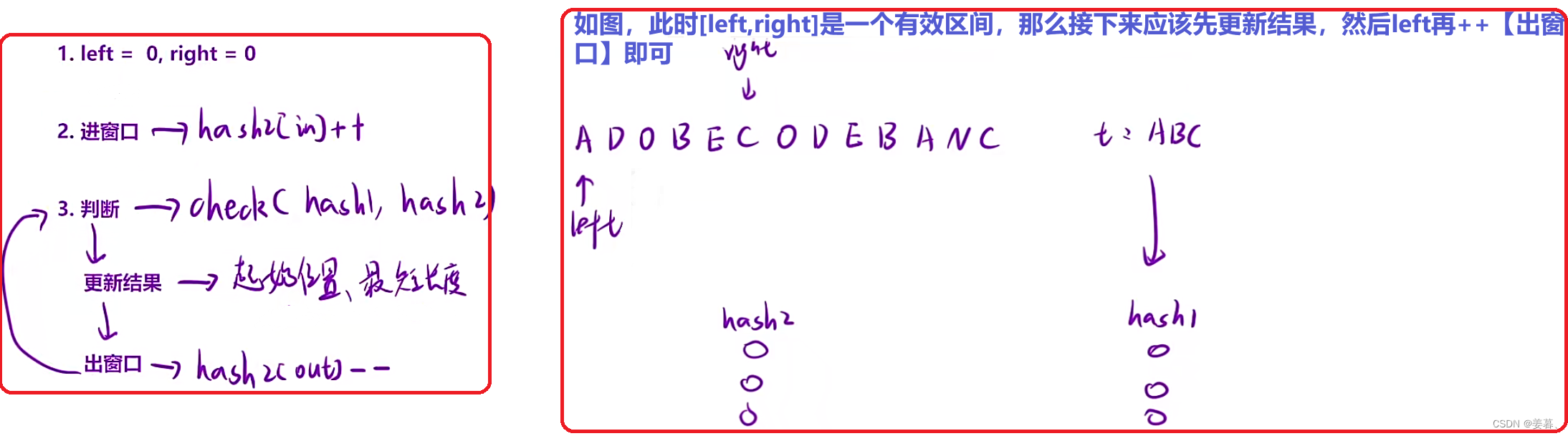

优化【为提高效率】?

class Solution {
public:
    string minWindow(string s, string t) {
        //能用数组哈希，最好用数组，用诸如unordered_map的容器来实现
        //哈希，会降级效率，况且本题范围只有字母
        int hash1[128] = { 0 };//统计每个字符出现次数
        int kinds = 0;//统计有效字符有多少种
        //在统计出现次数的同时统计种类
        for (auto ch : t) if (hash1[ch]++ == 0) kinds++;
        
        int hash2[128] = { 0 };//统计窗口内每个字符出现次数
        int minlen = INT_MAX, begin = -1;//最小长度和起始位置
        for (int left = 0, right = 0, count = 0; right < s.size(); right++)
        {
            //count记录窗口内有效字符的种类
            //进窗口+维护count
            char in = s[right];
            if (++hash2[in] == hash1[in]) count++;
            //出窗口+维护count【在种类==count时出窗口】
            while (kinds == count)
            {
                //出窗口前先更新结果
                if (right - left + 1 < minlen)
                {
                    minlen = right - left + 1;
                    begin = left;//最小覆盖子串的起始位置
                }
                //出窗口
                char out = s[left++];
                if (hash2[out]-- == hash1[out]) count--;
            }
        }
        if (begin == -1) return "";
        else return s.substr(begin, minlen);
    }
};

---