【算法实验】实验六

实验6-1 硬币找钱问题—贪心

问题描述：

　　设有6 种不同面值的硬币，各硬币的面值分别为5 分，1 角，2 角，5 角，1 元，2 元。现要用这些面值的硬币来购物和找钱。购物时可以使用的各种面值的硬币个数存于数组Coins［1:6 ］中，商店里各面值的硬币有足够多。在1 次购物中希望使用最少硬币个数。

　　例如，1 次购物需要付款0.55 元，没有5 角的硬币，只好用2*20+10+5 共4 枚硬币来付款。如果付出1 元，找回4 角5 分，同样需要4 枚硬币。但是如果付出1.05 元（1 枚1 元和1 枚5 分），找回5 角，只需要3 枚硬币。这个方案用的硬币个数最少。

编程任务：

　　对于给定的各种面值的硬币个数和付款金额，编程计算使用硬币个数最少的交易方案。

数据输入：

由文件input.txt 给出输入数据。每一行有6 个整数和1 个有2 位小数的实数。分别表示

可以使用的各种面值的硬币个数和付款金额。文件以6 个0 结束。

结果输出:

　　将编程计算出的最少硬币个数输出到文件output.txt 。结果应分行输出，每行一个数据。如果不可能完成交易，则输出”impossible”。

输入文件示例

input.txt

2 4 2 2 1 0?? 0.95

2 4 2 0 1 0?? 0.55

0 0 0 0 0 0

输出文件示例

output.txt

2

3

#include<bits/stdc++.h> 
const int N = 20000 ;
int ch[N]; 
int dp[N]; // dp[i]为当前拥有的硬币数量条件下表示面值为i的最少硬币个数
int v[ 6 ] = { 1 , 2 , 4 , 10 , 20 , 40 }; // 每种硬币对应面值，依次为1，2,4,10,20,40个五分，即5,10,20,50,100,200；
int nm[ 6 ]; // 对应于当前拥有的每种硬币个数
void init() // 计算ch[i]
{
	int i,j;
	for (i = 0 ;i < N;i ++ )ch[i] =- 1 ;
	ch[ 0 ] = 0 ;
	for (i = 0 ;i < 6 ;i ++ )
	{
		for (j = v[i];j < N;j ++ ) 
		{
			if (ch[j - v[i]] !=- 1 )
			{
				int temp = ch[j - v[i]] + 1 ;
				if (ch[j] ==- 1 || temp < ch[j])ch[j] = temp;
			}
		}
	}
}
int main()
{
	init(); 

	while (scanf( " %d%d%d%d%d%d " , & nm[ 0 ], & nm[ 1 ], & nm[ 2 ], & nm[ 3 ], & nm[ 4 ], & nm[ 5 ]) != EOF)
	{
		int sum = 0 ;
		int kk;
		for (kk = 0 ;kk < 6 ;kk ++ )sum += nm[kk];
		if (sum == 0 ) break ;
		double weight;
		scanf( " %lf " , & weight);
		weight = weight * 100 ;
		int w = int (weight + 0.0000001 ); 	
		if (w % 5 != 0 ) 
		{
			printf( " impossible\n " );
			continue ;
		}
		else
			w = w / 5 ;
		int i,j;
		memset(dp, - 1 , sizeof (dp));
		dp[ 0 ] = 0 ;
		int bigger = 0 ;
		for (i = 0 ;i < 6 ;i ++ )//计算顾客支付面值i需要的最少硬币数dp[i]
		{
			while (nm[i] -- ) 
			{
				bigger = bigger + v[i];
				for (j = bigger;j >= v[i];j -- )
				{
					if (dp[j - v[i]] !=- 1 )
					{
						int temp = dp[j - v[i]] + 1 ;
						if (dp[j] ==- 1 || temp < dp[j])
						{
							dp[j] = temp;
						}
					}
				}	
			}
		}
		int ans =- 1 ;
		for (i = w;i <= bigger;i ++ )//寻找最少硬币组合
		{
			if (dp[i] !=- 1 )
			{
				int need = i - w;
				if (ch[need] !=- 1 )
				{
					int temp = dp[i] + ch[need];
					if (ans ==- 1 || ans > temp)ans = temp;
				}
			}
		}
		if (ans !=- 1 )
			printf( " %d\n " ,ans);
		else
			printf( " impossible\n " );
	}
	return 0 ;
}

解决思路：

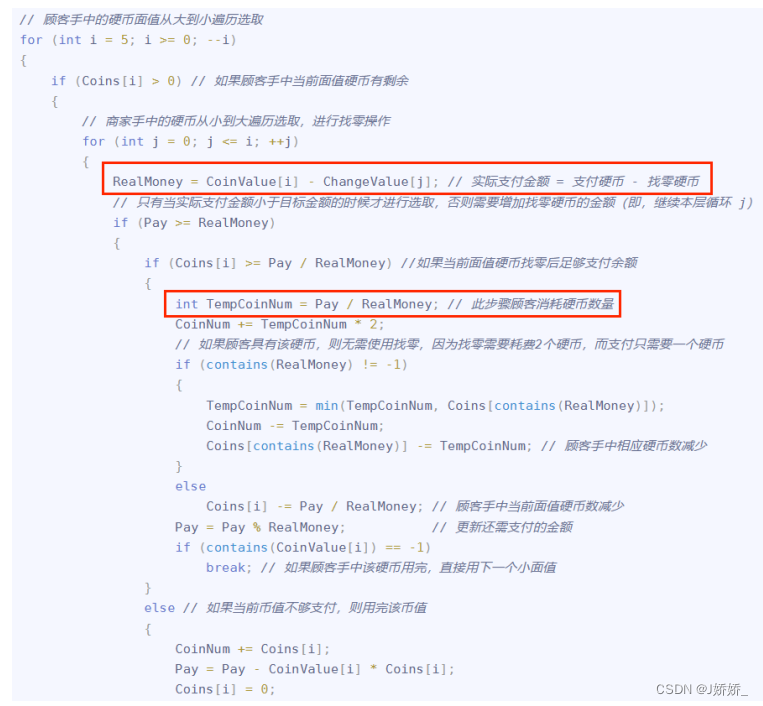
首先，我们要明确一下贪心算法的思想：每次尽可能选取面值最大的硬币，直到无法选取为止。这样可以保证找钱的硬币数量最少。

根据这个思想，我们可以先对硬币的面值按照从大到小的顺序进行排列，即2元、1元、5角、2角、1角和5分。然后，对于需要找的钱数，

我们从大到小依次考虑每种面值的硬币，先使用尽可能多的最大面值硬币，然后再考虑次大面值硬币，以此类推，直到钱数为0为止。

具体的步骤如下：

1.对硬币面值进行排序，顺序为2元，1元，5角，2角，1角，5分]。

2.对于需要找的钱数，从大到小依次考虑每种面值的硬币。

3.对于每种面值的硬币，先使用尽可能多的最大面值硬币，直到这种面值的硬币用完或者钱数不足该面值硬币的数量。

4.如果该种面值的硬币用完了，就考虑下一种面值的硬币。

5.重复以上步骤，直到钱数为0为止。

需要注意的是，在使用每种面值的硬币时，我们需要判断当前购物时可用的该种面值硬币数量是否足够，如果不够，则需要向下一种面值

的硬币继续考虑。

在实际操作中，我们可以设计一个循环，每次选择当前最大面值的硬币，然后扁历整个硬币数组，依次从当前最大面值的硬币个数到0

个，尝试找到一种可行的方案。如果可以找到一种方案，就更新钱数和对应的硬币数量。如果遍历完整个硬币数组仍然无法找到方案，则

说明无法完成找钱操作。

?

实验6-2 会场安排问题

问题描述：

　　假设要在足够多的会场里安排一批活动，并希望使用尽可能少的会场。设计一个有效的贪心算法进行安排。(这个问题实际上是著名的 。若将每一个活动作为图的一个顶点，不相容活动间用边相连。使相邻顶点着有不同颜色的最小着色数，相应于要找的最小会场数。)

编程任务：

　　对于给定的k 个待安排的活动，编程计算使用最少会场的时间表。

数据输入：

　　由文件input.txt 给出输入数据。第一行有1 个正整数k，表示有k 个待安排的活动。接下来的k 行中，每行有2 个正整数，分别表示k 个待安排的活动开始时间和结束时间。时间以0 点开始的分钟计。

结果输出:

　　将编程计算出的最少会场数输出到文件output.txt 。

输入文件示例输出文件示例

input.txt?????????????????????? output.txt

5???????????????????????????? 3

1 23

12 28

25 35

27 80

36 50

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int N = 1e4 + 5;
int n, a[N], b[N], ans;

int main() {
    // 打开输入文件
    freopen("input.txt", "r", stdin);
    // 从文件读取输入
    scanf("%d", &n);
    for(int i = 0; i < n; ++i) 
        scanf("%d%d", &a[i], &b[i]);

    sort(a, a + n);
    sort(b, b + n);

    int j = 0;
    ans = 0;
    for(int i = 0; i < n; ++i) {
        if(a[i] < b[j]) ans++;
        else j++;
    }

    // 打开输出文件
    freopen("output.txt", "w", stdout);
    // 向文件写入输出
    printf("%d", ans);

    // 关闭文件
    fclose(stdin);
    fclose(stdout);

    return 0;
}

算法具体描述：

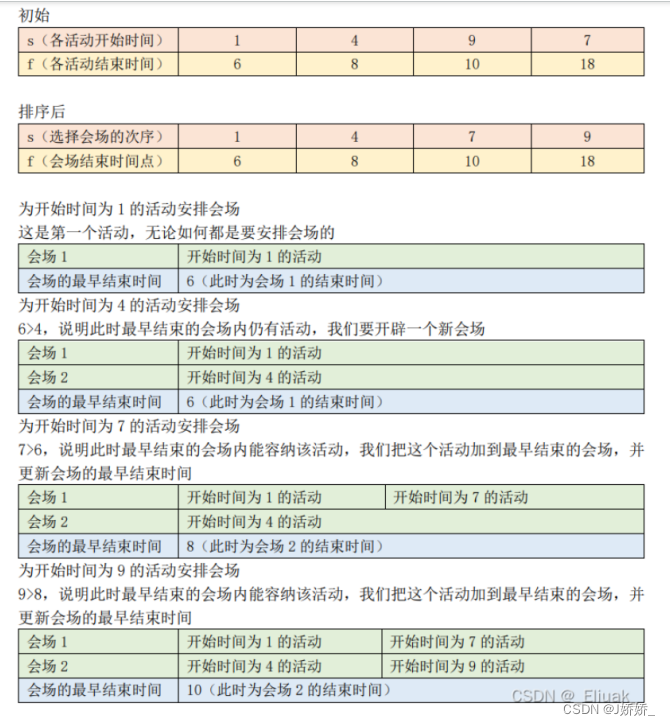
1）用数组s和f分别存储各活动的开始时间和结束时间，将s按非递减排序，该次序为各活动选择会场的次序；将f按非递减排序, 由于会场的结束时间由活动的结束时间决定，排序后的数组也是会场的结束时间点。

2）先为最早开始的活动开辟一个会场，此时会场的最早结束时间为该活动的结束时间，然后遍历剩下的活动，对于每个活动，判断当前最早结束的会场内是否仍有活动（即会场的最早结束时间大于该活动的开始时间），如果有，开辟一个新会场；如果没有，说明当前最早结束的会场能容纳当前的活动，更新会场的结束时间点，保证最早结束的会场最先开始下一个活动。

举例

设有4个活动，每个活动的开始和结束时间分别为{1, 6}, {4, 8}, {9, 10}, {7, 18}

实验6-3 文件压缩（Huffman Tree）

【问题描述】给定一个文件，文件由n个字符组成，但他们出现的频度不相同。要求对该文件中的字符集构造哈夫曼树，并计算编码后的文件长度。 【输入形式】

输入的第1行有1个数字n，表示文件中总的字符个数。接下来1行中有n个数字，分别表示n个字符出现的频度。 【输出形式】

输出1行包含1个数字，表示使用哈夫曼编码后该文件的长度。 【样例输入】

5

20 7 10 4 18 【样例输出】

129 【样例说明】

使用哈夫曼编码后，各字符的编码长度分别为2 3 2 3 2，文件长度为220+37+210+34+2*18=129

#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,ans;
int num[100100];
priority_queue<int>q;
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;++i)
	{
		int x;
		scanf("%d",&x);
		q.push(-x);
	}
	while(q.size()>1)
	{
		int cur=q.top();
		q.pop();
		int cur2=q.top();
		q.pop();
		int sum=cur+cur2;
		q.push(sum);
		ans+=-sum;
	}
	printf("%d",ans);
	return 0;
}