Grind75第13天 | 208.实现Trie、54.螺旋矩阵、721.账户合并

208.实现Trie

题目链接：https://leetcode.com/problems/implement-trie-prefix-tree

解法：

这个题非常经典，背下来。

首先需要自己实现Node的类，属性为children和是否为单词的标记，再去初始化Trie的类。

在插入和查询的过程中，都要不断让指针指向children。

参考题解：实现Trie

边界条件：无

class TrieNode:
    def __init__(self):
        self.children = {}
        self.is_word = False

class Trie:
    def __init__(self):
        self.root = TrieNode()

    def insert(self, word: str) -> None:
        node = self.root
        for c in word:
            if c not in node.children:
                node.children[c] = TrieNode()
            node = node.children[c]
        node.is_word = True

    def search_prefix(self, word):
        node = self.root
        for c in word:
            if c not in node.children:
                return None
            node = node.children[c]
        return node

    def search(self, word: str) -> bool:
        node = self.search_prefix(word)
        return node is not None and node.is_word

    def startsWith(self, prefix: str) -> bool:
        node = self.search_prefix(prefix)
        return node is not None


# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)

54.螺旋矩阵

题目链接：https://leetcode.com/problems/spiral-matrix

解法：

顺时针打印矩阵的顺序是?“从左向右、从上向下、从右向左、从下向上”?循环。代码实现就是去模拟这个过程。

思路很直观，但是要处理好最后（最内部）的一个元素、一行或者一列，还是比较有讲究。如果循环时的边界处理不当，那么最内部的元素、一行或一列可能需要单独处理，这样就麻烦了。

按照以下的遍历顺序去处理，注意到从左到右和其他的三个方向不一样，从左到右把一行的所有元素都遍历了，而其他方向的遍历则少一个元素。这样却比较好处理最后的元素。

把代码运行一遍就理解了。

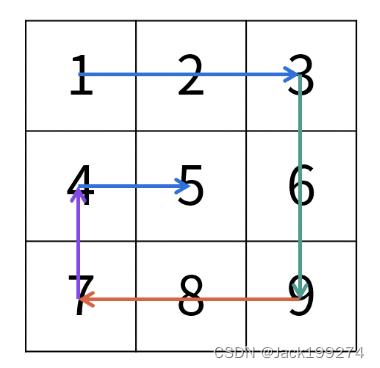
参考题解：螺旋矩阵

边界条件：

时间复杂度：O(mn)，其中?m和?n分别是输入矩阵的行数和列数

空间复杂度：O(1)

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        if not matrix: return []
        l, r, t, b = 0, len(matrix[0])-1, 0, len(matrix)-1
        res = []
        while True:
            for i in range(l, r+1):
                res.append(matrix[t][i])
                # t要马上加1，因为下面的遍历是从下一行开始的
            t += 1
            if t > b: break

            for i in range(t, b+1):
                res.append(matrix[i][r])
            r -= 1
            if l > r: break

            for i in range(r, l-1, -1):
                res.append(matrix[b][i])
            b -= 1
            if t > b:break

            for i in range(b, t-1, -1):
                res.append(matrix[i][l])
            l += 1
            if l > r:
                break

        return res

721.账户合并

题目链接：https://leetcode.com/problems/accounts-merge

解法：

并查集基础：图论——并查集(详细版)_哔哩哔哩_bilibili

并查集的代码是作为模板直接用的，有三个部分：初始化，查找父节点（寻根），合并。功能一般是用于查询两个节点是不是有相同的根（相同的集合中）。

一个容易理解的例子是：给出若干个pair对（张三和张五，李四和李六），pair对表示这俩人是亲戚关系，那么可以构建亲戚图谱（合并操作）。再给出一个pair对（张三和李六），问他们俩是不是亲戚（查询是否有相同的根）。

对于并查集的优化有路径压缩和按秩合并。路径压缩实现简单，这里只用了路径压缩。

具体实现直接看代码比较直观。

参考题解：并查集

边界条件：

时间复杂度：O(nlogn)，其中?n是不同邮箱地址的数量，logn 是路径压缩的复杂度。另外对邮箱排序的复杂度也是O(nlogn)

空间复杂度：O(n)

class UnionFind:
    def __init__(self, n):
        self.parent = list(range(n))

    def find(self, idx):
        # 查找idx的根节点
        if self.parent[idx] != idx:
            self.parent[idx] = self.find(self.parent[idx])
        return self.parent[idx]

    def union(self, idx1, idx2):
        # 找到idx1和idx2的根节点，然后合并
        root1 = self.find(idx1)
        root2 = self.find(idx2)
        self.parent[root1] = root2

class Solution:
    def accountsMerge(self, accounts: List[List[str]]) -> List[List[str]]:
        email_index = {}
        email_name = {}

        # 把email转化为idx，以便直接使用并查集的模板
        for account in accounts:
            name = account[0]
            for email in account[1:]:
                if email not in email_index:
                    email_index[email] = len(email_index)
                    email_name[email] = name

        # 使用并查集合并邮箱
        uf = UnionFind(len(email_index))
        for account in accounts:
            first_idx = email_index[account[1]]
            for email in account[2:]:
                next_idx = email_index[email]
                uf.union(first_idx, next_idx)
            
        # 把作为根节点的邮箱所连接的所有邮箱收集起来（包含本身）
        idx_emails = defaultdict(list)
        for email, idx in email_index.items():
            root = uf.find(idx)
            idx_emails[root].append(email)

        # 添加name，获取结果
        res = []
        for emails in idx_emails.values():
            res.append([email_name[emails[0]]] + sorted(emails))
        return res