Speech | 人工智能中语音质量评估方法详解及代码

音频级别	MOS值	评价标准
优	4.0~5.0	很好，听得清楚；延迟小，交流流畅
良	3.5~4.0	稍差，听得清楚；延迟小，交流欠流畅，有点杂音
中	3.0~3.5	还可以，听不太清；有一定延迟，可以交流
差	1.5~3.0	勉强，听不太清；延迟较大，交流需要重复多遍
劣	0~1.5	极差，听不懂；延迟大，交流不通畅

一般MOS应为4或者更高，这可以被认为是比较好的语音质量，若MOS低于3.6，则表示大部分被测不太满意这个语音质量。?

MOS测试一般要求：

足够多样化的样本（即试听者和句子数量）以确保结果在统计上的显著；
控制每个试听者的实验环境和设备保持一致；
每个试听者遵循同样的评估标准。
?

1.2.CMOS?

comparative mean opinion score的缩写，naturalspeech论文中提出的相关概念，通过采用“平均意见分”（Mean Opinion Score, MOS）来衡量 TTS 质量，因为MOS 对于区分声音质量的差异不是非常敏感，只是对两个系统的每条句子单独打分，没有两两互相比较。而 CMOS（Comparative MOS）在评测过程中可以对两个系统的句子两两对比并排打分，并且使用七分制来衡量差异，所以对质量差异更加敏感。

1.3.ABX Test

ABX测试是一种常用的主观评估方法，用于比较两个声音样本中哪一个更接近于第三个参考样本。参与者在三次听觉对比中选择A或B与X相匹配。这种测试常用于评估音频编解码器、语音合成系统等的效果。

1.4.MUSHRA（MUltiple Stimuli with Hidden Reference and Anchor）

MUSHRA是一种主观评估方法，用于比较多个音频样本（被评估的）与隐藏的参考音频样本。评估者需要对参考音频和每个样本进行评分，以确定哪个样本最接近参考音频。

客观评价方法

1.5.MCD

论文题目：Mel-cepstral distance measure for objective speech quality assessment

论文地址：Mel-cepstral distance measure for objective speech quality assessment | IEEE Conference Publication | IEEE Xplore

Github：MattShannon/mcd: Mel cepstral distortion (MCD) computations in python. (github.com)

梅尔倒谱畸变（MCD）是衡量两个序列的不同程度的量度梅尔·塞普斯特拉（Mel Cepstra）是用于评估参数语音合成系统的质量，包括统计参数语音合成系统，其想法是合成的 mel 倒谱序列和天然的 mel 倒谱序列之间的 MCD 越小，合成语音更接近于再现自然语音。它绝不是评估合成质量的完美指标语音，但通常与其他指标结合使用是一个有用的指标。

MCD的计算方法如下：

提取MFCCs：首先，从合成语音和目标语音中提取MFCCs。这涉及将语音信号转换为频谱表示，然后应用梅尔滤波器组并使用倒谱分析获得MFCC系数。
计算距离：接下来，通过比较合成语音和目标语音之间的MFCC系数来计算距离。通常使用欧几里得距离（Euclidean distance）或动态时间规整（Dynamic Time Warping，DTW）等方法来衡量两个语音信号之间的相似性或差异。
求取平均值：对所有帧（或时间段）的距离进行平均，得到整个语音信号的MCD分数。MCD分数越低表示合成语音和目标语音之间的差异越小，质量越高。

MCD 是衡量语音合成质量的一种常用指标，但它只是梅尔倒谱系数之间的距离度量，不能完全代表语音合成的质量。在使用 MCD 时需要注意，它是一种客观评价指标，还需要结合其他指标和主观评价来全面评估语音合成系统的性能。

?但研究发现，它与人们主观感受到的音质的相关性并不够强。在我看到的几乎所有论文中，没有使用此方法·

在MCD（Mel Cepstral Distortion）的计算过程中，三种模式（plain、dtw、dtw_sl）表示了不同的计算方式，主要体现在计算梅尔倒谱距离时的方法上：

Plain（普通模式）：

这种模式下的 MCD 计算是基于梅尔倒谱系数的直接欧氏距离。它是最简单、直接的计算方式，没有额外的变换或校正。

DTW（动态时间规整）：

动态时间规整是一种通过比较两个序列的相似性的方法，在MCD中，使用DTW来对齐两个序列，以最小化它们之间的距离。它允许序列在时间轴上有一定程度的弹性对齐，可以处理一些在时间上略微错位的情况。

DTW_SL（DTW with Straight-line Constraint，带直线约束的DTW）：

这种模式下的DTW在进行对齐时，增加了直线约束。这意味着对齐过程中的路径是在不太影响整体相似性的情况下，尽量保持直线，从而减少了可能不必要的弯曲和错位。

1.6.PESQ（Perceptual Evaluation of Speech Quality）

PESQ是一种客观评估方法，用于测量语音质量。它计算原始语音和经过处理（压缩、编码等）的语音之间的差异，以提供语音质量的分数。这个指标常用于衡量语音编解码器或通信系统的性能。

1.7.STOI（Short-Time Objective Intelligibility）

STOI 是用于测量语音清晰度和可懂度的客观评价方法，特别适用于测量语音合成的可懂度和识别率。

STOI（Short-Time Objective Intelligibility）是一种用于测量语音信号质量的客观评估指标。它旨在衡量清晰度和可懂度之间的相关性，是一种针对语音信号的质量评估方法。

STOI 主要通过比较原始语音和失真/噪声语音之间的频谱相关性来评估语音信号的可懂度。它的核心思想是，在人耳感知语音时，大脑会对频谱相关性进行敏感的处理。因此，STOI利用了频谱之间的相关性来估计语音信号的清晰度和可懂度。

这个方法的一般步骤如下：

短时傅立叶变换（STFT）：语音信号被分成短时间段，并进行STFT，将信号转换成频谱形式。
频谱相关性计算：对原始语音和失真/噪声语音的频谱进行相关性计算。通常是通过计算频谱帧之间的相似度来衡量。
相关性平均：计算所有频谱帧的相关性，并求得平均值，作为整个信号的STOI评分。

STOI的结果介于0到1之间，数值越接近1表示语音信号的可懂度越高，越接近0表示可懂度较低。

这个评价方法在语音信号的音质、清晰度和可懂度方面提供了一种定量的评估，通常用于语音信号处理领域，特别是在语音增强、降噪、编解码和语音合成等应用中，可以帮助评估算法的效果。

1.8.LLR（Log Likelihood Ratio）

用于评估模型生成的语音是否属于给定的语音分布。

2.在语音任务中的使用【详细代码】

语音合成
语音转换
语音克隆

语音合成中常使用的主要是MOS和CMOS，但是因为主观性比较大，差异可能也比较大~

2.1.MOS计算


import math
import numpy as np
import pandas as pd
from scipy.linalg import solve
from scipy.stats import t


def calc_mos(data_path: str):
    '''
    计算MOS，数据格式：MxN，M个句子，N个试听人，data_path为MOS得分文件，内容都是数字，为每个试听的得分
    :param data_path:
    :return:
    '''
    data = pd.read_csv(data_path)
    mu = np.mean(data.values)
    var_uw = (data.std(axis=1) ** 2).mean()
    var_su = (data.std(axis=0) ** 2).mean()
    mos_data = np.asarray([x for x in data.values.flatten() if not math.isnan(x)])
    var_swu = mos_data.std() ** 2

    x = np.asarray([[0, 1, 1], [1, 0, 1], [1, 1, 1]])
    y = np.asarray([var_uw, var_su, var_swu])
    [var_s, var_w, var_u] = solve(x, y)
    M = min(data.count(axis=0))
    N = min(data.count(axis=1))
    var_mu = var_s / M + var_w / N + var_u / (M * N)
    df = min(M, N) - 1  # 可以不减1
    t_interval = t.ppf(0.975, df, loc=0, scale=1)  # t分布的97.5%置信区间临界值
    interval = t_interval * np.sqrt(var_mu)
    print('{} 的MOS95%的置信区间为：{} +—{} '.format(data_path, round(float(mu), 3), round(interval, 3)))


if __name__ == '__main__':
    data_path = ''
    calc_mos(data_path)

2.2.使用MCD进行计算

单语音对比

from pymcd.mcd import Calculate_MCD
 
# instance of MCD class
# three different modes "plain", "dtw" and "dtw_sl" for the above three MCD metrics
mcd_toolbox = Calculate_MCD(MCD_mode="plain")

 
# two inputs w.r.t. reference (ground-truth) and synthesized speeches, respectively
# 同样的元语音和生成语音对比
mcd_value = mcd_toolbox.calculate_mcd("1.wav", "gen_1.wav")
print(mcd_value)

批量

from pymcd.mcd import Calculate_MCD
import os
import numpy as np


def batch_calculate_mcd(original_folder, generated_folder):
    mcd_toolbox = Calculate_MCD(MCD_mode="dtw")
    mcd_values = []

    # 获取文件夹中的文件列表，并按照文件名排序
    original_files = sorted(os.listdir(original_folder))
    generated_files = sorted(os.listdir(generated_folder))

    # 逐对比较语音文件
    for orig_file, gen_file in zip(original_files, generated_files):
        orig_path = os.path.join(original_folder, orig_file)
        gen_path = os.path.join(generated_folder, gen_file)

        # 进行MCD值的计算
        mcd_value = mcd_toolbox.calculate_mcd(orig_path, gen_path)
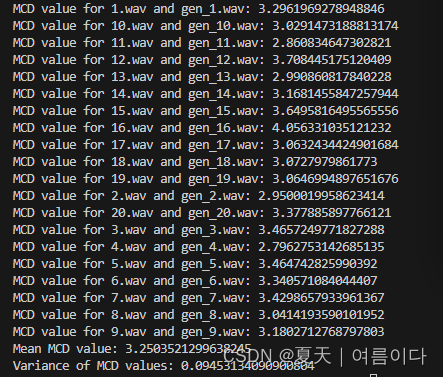
        print(f"MCD value for {orig_file} and {gen_file}: {mcd_value}")
        mcd_values.append(mcd_value)

    # 计算均值和方差
    mean_mcd = np.mean(mcd_values)
    variance_mcd = np.var(mcd_values)

    print(f"Mean MCD value: {mean_mcd}")
    print(f"Variance of MCD values: {variance_mcd}")

original_folder_path = './original_data'
generated_folder_path = './gen_data'


batch_calculate_mcd(original_folder_path, generated_folder_path)

2.3.STOI

单语音对比

# pip install scipy numpy

import numpy as np
from scipy.io import wavfile
from scipy.signal import stft

def stoi(x, y, fs):
    win_len = int(fs * 0.025)  # 窗长为25ms
    hop_len = int(fs * 0.010) # 窗移为10ms

    _, _, Pxo = stft(x, fs=fs, nperseg=win_len, noverlap=hop_len)
    _, _, Pyo = stft(y, fs=fs, nperseg=win_len, noverlap=hop_len)

    # 计算时间频率上的STOI
    stoi_values = []
    for i in range(Pxo.shape[1]):
        Pxo_i = np.abs(Pxo[:, i])
        Pyo_i = np.abs(Pyo[:, i])

        
        Rxy = np.sum(Pxo_i * Pyo_i) / np.sqrt(np.sum(Pxo_i ** 2) * np.sum(Pyo_i ** 2))
        stoi_values.append(Rxy)

    return np.mean(stoi_values)

# 读取原始语音和生成语音
rate_orig, orig_audio = wavfile.read('original_data/1.wav')
rate_gen, gen_audio = wavfile.read('gen_data/gen_1.wav')


if rate_orig != rate_gen:
    print("If the sampling rate of the original audio and the generated audio are different, please adjust the sampling rate of the generated audio to the sampling rate of the original audio.")


# 计算STOI值
stoi_value = stoi(orig_audio, gen_audio, rate_orig)
print("stoi value:", stoi_value)

?批量对比

import os
import numpy as np
from scipy.io import wavfile
from scipy.signal import stft

def stoi(x, y, fs):
    win_len = int(fs * 0.025)  # 窗长为25ms
    hop_len = int(fs * 0.010)  # 窗移为10ms

    _, _, Pxo = stft(x, fs=fs, nperseg=win_len, noverlap=hop_len)
    _, _, Pyo = stft(y, fs=fs, nperseg=win_len, noverlap=hop_len)

    stoi_values = []
    for i in range(Pxo.shape[1]):
        Pxo_i = np.abs(Pxo[:, i])
        Pyo_i = np.abs(Pyo[:, i])

        # 计算频谱之间的相关性
        Rxy = np.sum(Pxo_i * Pyo_i) / np.sqrt(np.sum(Pxo_i ** 2) * np.sum(Pyo_i ** 2))
        stoi_values.append(Rxy)

    return np.mean(stoi_values)

def calculate_stoi_for_files(original_folder, generated_folder):
    original_files = os.listdir(original_folder)
    generated_files = os.listdir(generated_folder)

    for orig_file, gen_file in zip(original_files, generated_files):
        orig_path = os.path.join(original_folder, orig_file)
        gen_path = os.path.join(generated_folder, gen_file)

        rate_orig, orig_audio = wavfile.read(orig_path)
        rate_gen, gen_audio = wavfile.read(gen_path)

        # 调整采样率...
        # 如果需要的话，进行采样率调整...

        # 计算STOI值
        stoi_value = stoi(orig_audio, gen_audio, rate_orig)
        print(f"STOI值 - {orig_file} vs {gen_file}: {stoi_value}")

# 原始语音和生成语音文件夹路径
original_folder_path = 'path_to_original_audio_folder'
generated_folder_path = 'path_to_generated_audio_folder'

# 计算STOI值
calculate_stoi_for_files(original_folder_path, generated_folder_path)

3.测试总结

3.1.在MCD测试中总结

模式为plain，测试了同一个说话人的三个不同语音语句，结果如下

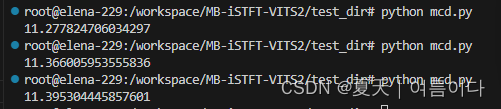
?而模式为dtw时

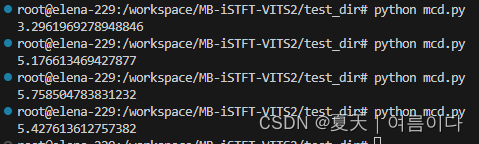
?第一个为真实生成，其他三个为不同语句，由此可见MCD的值并不能完全代表语音生成结果的还坏！

3.2.在STIO测试中总结

数据对比时，容易出现nan和index索引问题，

【扩展】

使用MCD值，求均值和方差，画出直方图

# pip install matplotlib seaborn

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np


# 语音和对应的数值
speeches = ['1', '2', '3', '4', '5', '6', '7', '8', '9', '10', '11', '12', '13', '14', '15', '16', '17', '18,','19', '20']
#data = np.random.rand(10, 10) 
data = [5,8,7,6,8,4,10,7,9,6,7,5,6,8,10,11,8,10,9,8]  # 与每个语音对应的数值

# 计算均值和方差
mean_value = np.mean(data)
variance_value = np.var(data)

# 创建直方图
plt.figure(figsize=(10, 6))  # 设置图的大小
x = np.arange(len(speeches))  # 使用语音的索引作为x轴
plt.bar(x, data, color='skyblue', edgecolor='black')  # 绘制直方图，设置颜色和边缘颜色
plt.xlabel('Speeches')  # x轴标签
plt.ylabel('Value')  # y轴标签
plt.title('Values for Each Speech')  # 设置标题

# 设置x轴标签为语音名称
plt.xticks(x, speeches)

# 显示均值和方差
plt.axhline(mean_value, color='red', linestyle='--', label=f'Mean: {mean_value:.2f}')  # 添加均值线
plt.axhline(mean_value + np.sqrt(variance_value), color='green', linestyle=':', label='Std Dev')  # 上方标准差线
plt.axhline(mean_value - np.sqrt(variance_value), color='green', linestyle=':', label='_nolegend_')  # 下方标准差线

plt.grid(axis='y')  # 只在y轴上显示网格线
plt.legend()  # 显示图例
plt.tight_layout()  # 调整布局
plt.show()  # 显示图表

文章来源:https://blog.csdn.net/weixin_44649780/article/details/135399901
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！