面试算法108：单词演变

题目

输入两个长度相同但内容不同的单词（beginWord和endWord）和一个单词列表，求从beginWord到endWord的演变序列的最短长度，要求每步只能改变单词中的一个字母，并且演变过程中每步得到的单词都必须在给定的单词列表中。如果不能从beginWord演变到endWord，则返回0。假设所有单词只包含英文小写字母。
例如，如果beginWord为"hit"，endWord为"cog"，单词列表为[“hot”，“dot”，“dog”，“lot”，“log”，“cog”]，则演变序列的最短长度为5，一个可行的演变序列为"hit"→"hot"→"dot"→"dog"→"cog"。

分析

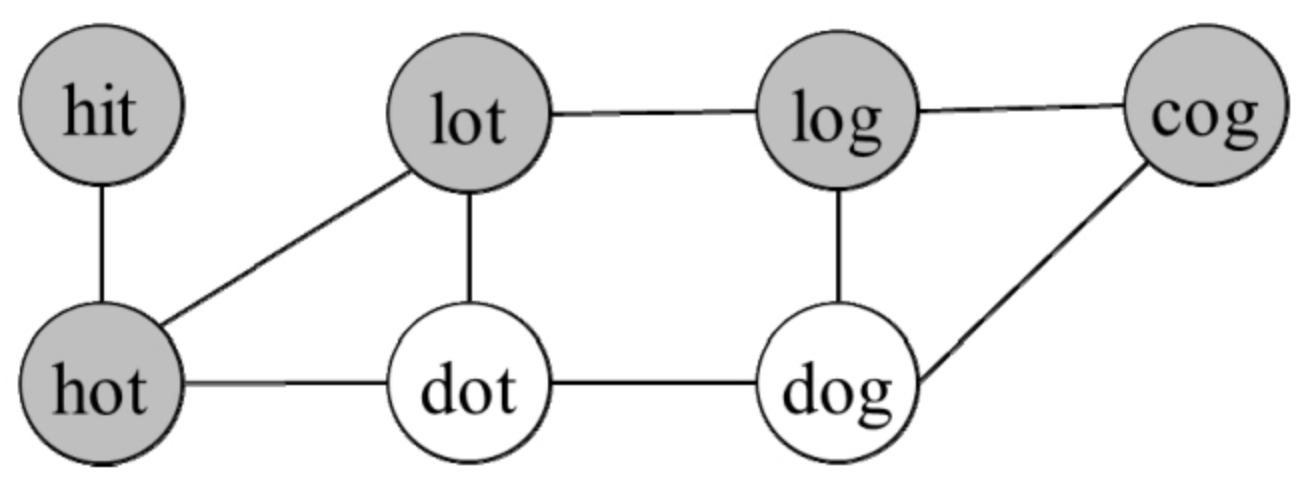
应用图相关算法的前提是找出图中的节点和边。这个问题是关于单词的演变的，所以每个单词就是图中的一个节点。如果两个单词能够相互演变（改变一个单词的一个字母能变成另一个单词），那么这两个单词之间有一条边相连。

为了求得两个节点之间的最短距离，常见的解法是用两个队列实现广度优先搜索算法。一个队列queue1中存放离起始节点距离为d的节点，当从这个队列中取出节点并访问的时候，与队列queue1中节点相邻的节点离起始节点的距离都是d+1，将这些相邻的节点存放到另一个队列queue2中。当队列queue1中的所有节点都访问完毕时，再访问队列queue2中的节点，并将相邻的节点放入queue1中。可以交替使用queue1和queue2这两个队列由近及远地从起始节点开始搜索所有节点。

解： 单向广度优先搜索

public class Test {
    public static void main(String[] args) {
        List<String> wordList = Arrays.asList("hot", "dot", "dog", "lot", "log", "cog");
        int result = ladderLength("hit", "cog", wordList);
        System.out.println(result);
    }

    public static int ladderLength(String beginWord, String endWord, List<String> wordList) {
        Queue<String> queue1 = new LinkedList<>();
        Queue<String> queue2 = new LinkedList<>();
        Set<String> notVisited = new HashSet<>(wordList);
        int length = 1;
        queue1.add(beginWord);
        while (!queue1.isEmpty()) {
            String word = queue1.remove();
            if (word.equals(endWord)) {
                return length;
            }

            List<String> neighbors = getNeighbors(word);
            for (String neighbor : neighbors) {
                if (notVisited.contains(neighbor)) {
                    queue2.add(neighbor);
                    notVisited.remove(neighbor);
                }
            }

            if (queue1.isEmpty()) {
                length++;
                queue1 = queue2;
                queue2 = new LinkedList<>();
            }
        }

        return 0;
    }

    private static List<String> getNeighbors(String word) {
        List<String> neighbors = new LinkedList<>();
        char[] chars = word.toCharArray();
        for (int i = 0; i < chars.length; i++) {
            char old = chars[i];

            for (char ch = 'a'; ch <= 'z'; ++ch) {
                if (old != ch) {
                    chars[i] = ch;
                    neighbors.add(new String(chars));
                }
            }

            chars[i] = old;
        }

        return neighbors;
    }

}