LeetCode 48 旋转图像

题目描述

旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

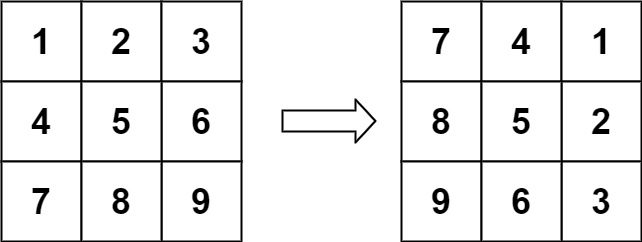
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

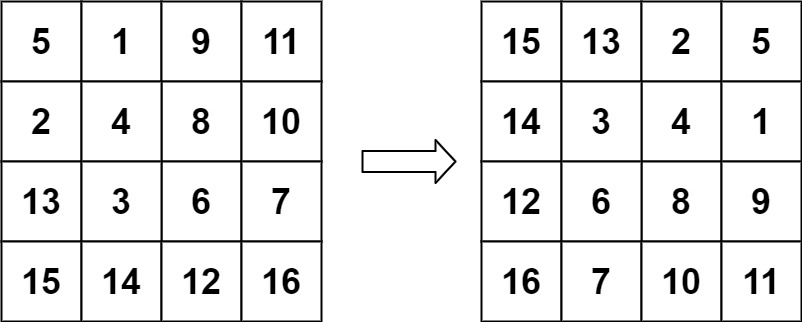
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

解法

1. 解法1：临时数组

旋转特点：

• 第一行而言，在旋转后，它出现在倒数第一列的位置；矩阵中的第二行而言，在旋转后，它出现在倒数第二列的位置
• 以此类推得到规律：对于矩阵中第 i 行的第 j 个元素，在旋转后，它出现在倒数第 i 列的第 j 个位置。
• 即：对于矩阵中的元素 matrix[row][col]，在旋转后，它的新位置为 matrix_new[col][n?row?1]

代码思路:

• 我们使用一个与 matrix 大小相同的辅助数组 matrix_new ，临时存储旋转后的结果。
• 然后遍历 matrix中的每一个元素，根据上述规则将该元素存放到 matrix_new中对应的位置。
• 在遍历完成之后，再将 matrix_new中的结果复制到原数组中即可。

java代码：

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        int[][] matrixNew = new int[n][n];
        for (int i = 0; i <n; i++) {
            for (int j = 0; j < n; j++) {
                matrixNew[j][n-i-1] = matrix[i][j];
            }
        }
        for (int i = 0; i <n; i++) {
            for (int j = 0; j < n; j++) {
                matrix[i][j] = matrixNew[i][j];
            }
        }
    }
}

复杂度

• 时间复杂度：O(N^2)， 其中 N 是 matrix的边长
• 空间复杂度：O(N^2)。

2. 解法2：用翻转代替旋转

思路：先水平轴翻转，再主对角线翻转，证明过程参考：旋转图像官方讲解

java代码：

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        // 水平翻转
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < n; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = temp;
            }
        }
        // 主对角线翻转
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }
}

复杂度

• 时间复杂度：O(N^2)， 其中 N 是 matrix的边长
• 空间复杂度：O(1)。