【数据结构入门精讲 | 第十八篇】考研408、企业面试图专项练习（一）

在上一篇中我们学习了图的相关知识点，在这一篇中我们进行图的专项练习。

判断题

1

选择两城市间最经济的航行路线用迪杰斯特拉算法（对）

2

从某顶点出发进行深度优先遍历，最先退出dfs过程的是拓扑序列的最后一个顶点。（对）

3

对任意一个图，从某顶点出发进行一次深度优先或广度优先遍历，可访问图的所有顶点。（错）
若存在回路，则结束遍历，剩下的节点就不能被访问。

4

检查有向图是否存在回路的一种方法是使用无前驱顶点优先算法对有向图进行拓扑排序。（ 对 ）

5
一个邻接矩阵如下：

0 1 1 0 1 0
1 0 0 1 0 0
1 0 0 0 1 1
0 1 0 0 1 0
1 0 1 1 0 1
0 0 1 0 1 0

若用广度优先进行遍历，则可能得到的顶点序列为？

解，由邻接矩阵可得：
第一行第二列、第一行第三列、第一行第五列为1，所以
1>2，1>3，1>5，即1>2>3>5
同理
2>1>4
3>1>5>6
4>2>5
5>1>3>4>6
6>3>5
所以1>2>4>5>6>3是可能的

6
如果G是有28条边的连通无向图，则顶点个数为多少？
解：除孤立点外，n个顶点构成的无向完全图最多有n(n-1)/2条
故解得n为8，加上孤立点，故顶点个数为9

7解析：图是非线性的，表示多对多的关系。

9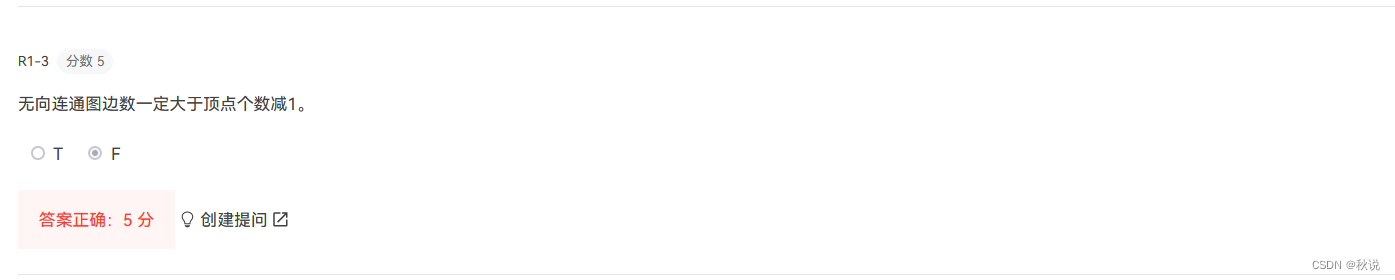

解析：无向连通图是指对图中任意顶点u，v，都存在路径使u、v连通。

o--o--o
这是无向连通图，边数为2，不会大于顶点数减一

10

11

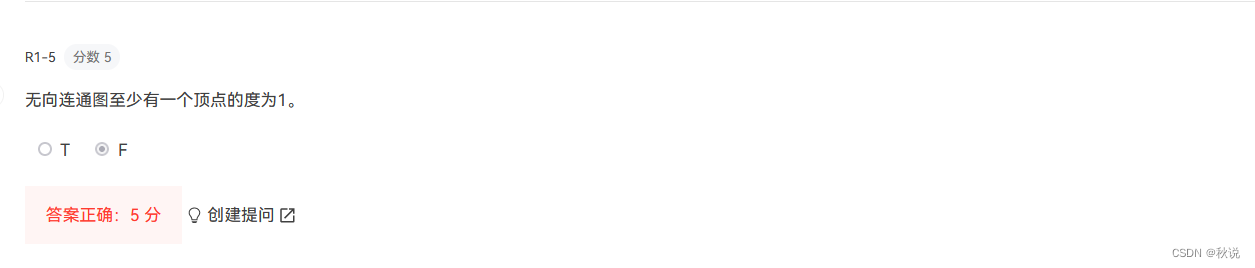
解析：
    o
   / \
  o - o
每个顶点的度为2  

12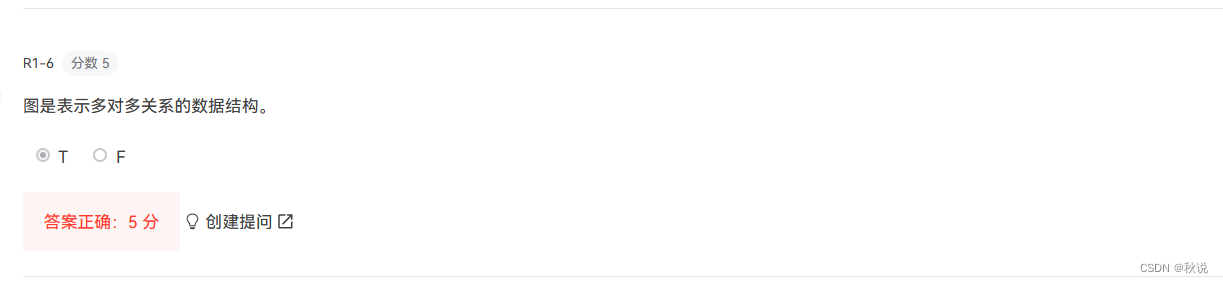
13

14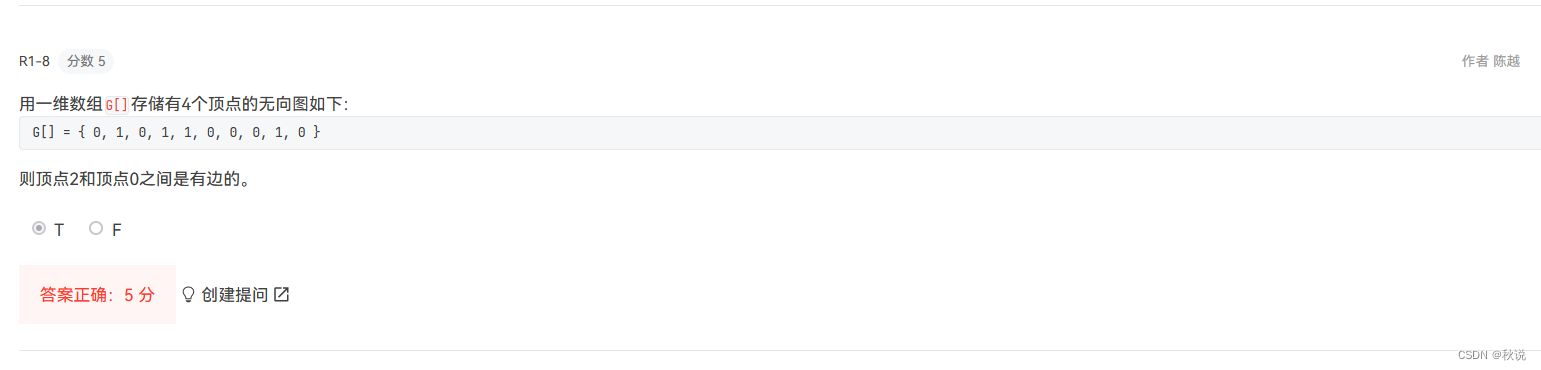

15、16

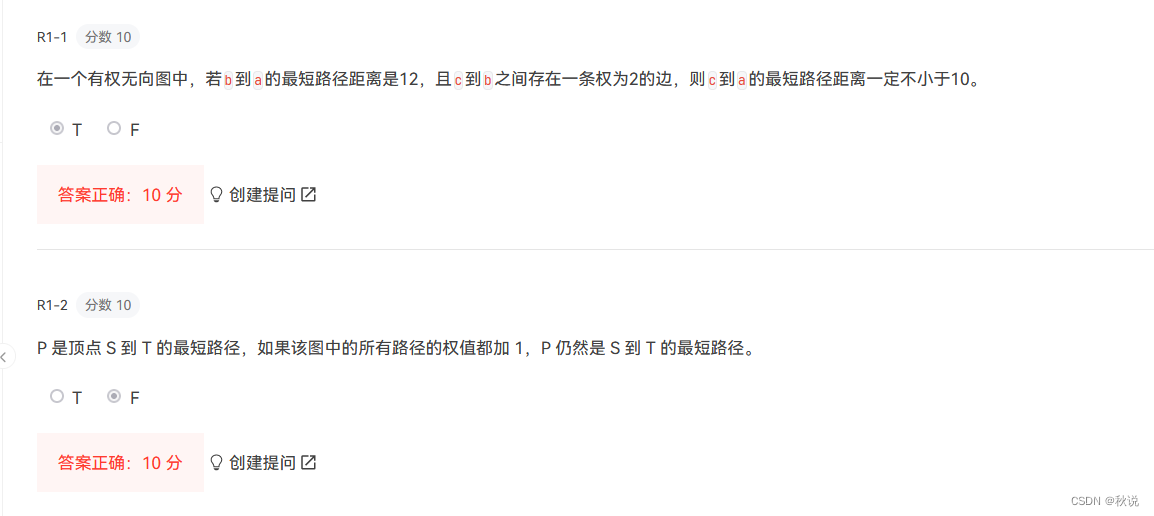
解析：
对于15，c可能在a、b之间，也可能在a、b之外，故对

16不再赘述。

17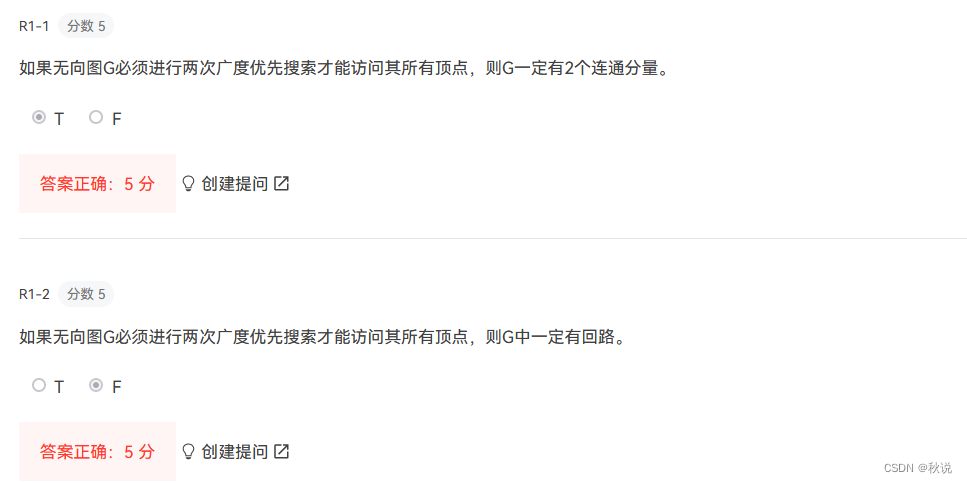

18

解析：不一定，如图，5到4的路径并不是最短路径

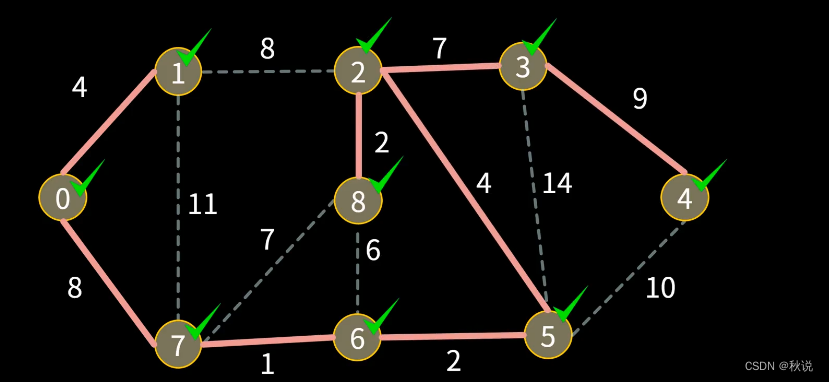
19

20

21

22
23若图G有环，则G不存在拓扑排序序列。（对）

解析：拓扑排序的前提是有向无环图

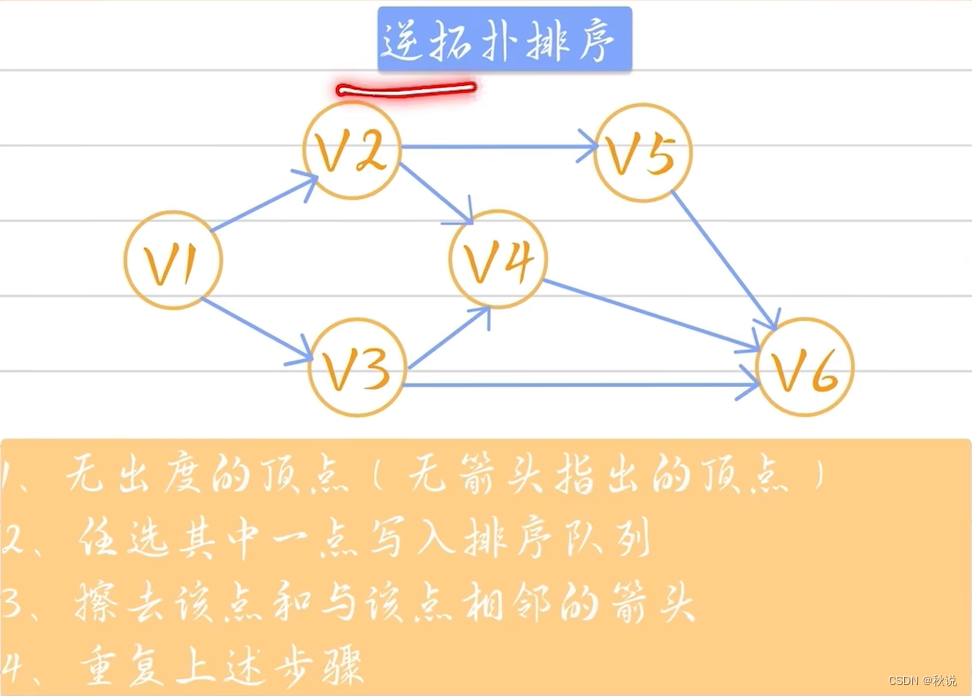
24如果从有向图 G 的每一点均能通过深度优先搜索遍历到所有其它顶点，该图一定不存在拓扑序列（对）

选择题

1.对于一个具有 N 个顶点，m条边的无向图，若采用邻接表来表示，则该邻接表的大小是？

对于无向图，每个顶点最多与其他 N-1 个顶点相连，因此邻接表的大小为 O(N)。而每条边都会在邻接表中占用一个节点，所以边的数量 m 也会影响邻接表的大小。综合起来，邻接表的大小是 O(m + N)。

2.采用邻接矩阵存储图时，广度优先搜索遍历算法的时间复杂度为 C

A. O（n） B. O（n+e） C. O（n^2） D. O（n^3）

3

矩阵为N阶矩阵，故选B

4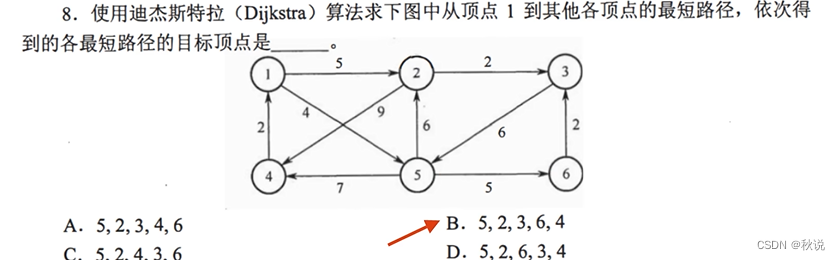

1到2 为5
1到3 为7
1到4 为11
1到5 为4
1到6 为9

排序得到4 5 7 9 11
即对应 5 2 3 6 4

5

6.如果从无向图的任一顶点出发进行一次深度优先搜索即可访问所有顶点，则该图一定是（连通图）

7.下列说法正确的是（ D ）。
A、连通分量是无向图的极小连通子图
B、生成树是无向图的极大连通子图
C、具有n个顶点，少于n-1条边的无向图可能是连通图
D、具有n个顶点，多于n-1条边的无向图必存在环

8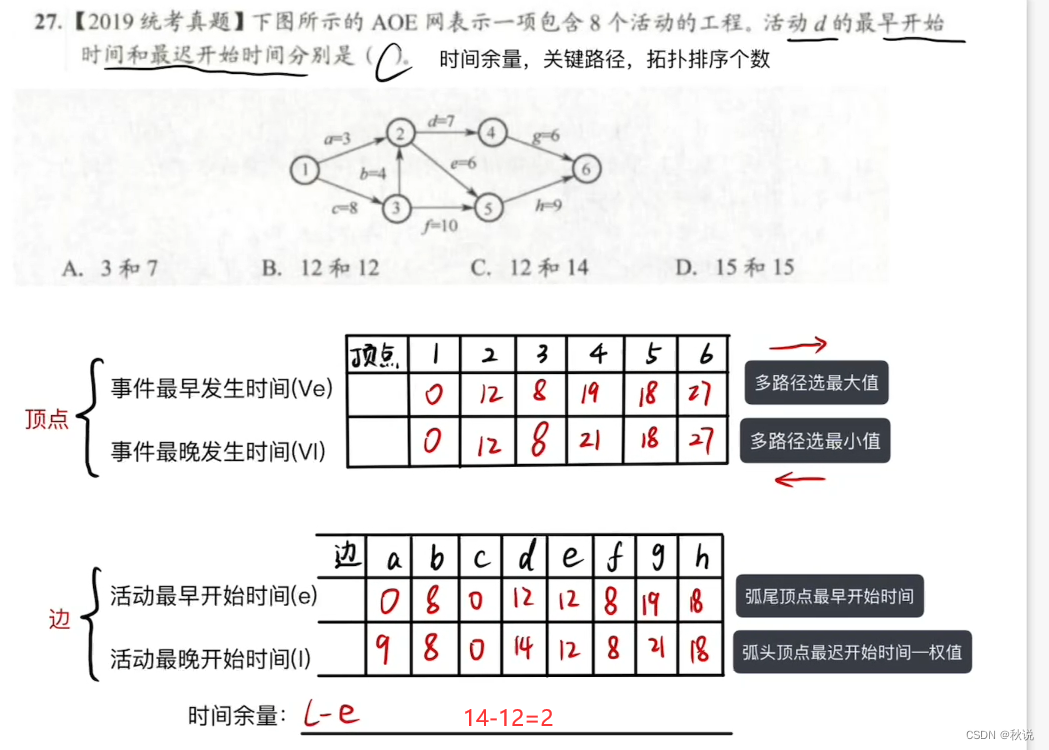

对于活动最早开始时间，找线段中没有箭头的一端，取该端的最早开始时间
例如b
b没有箭头的一端为3
3的最早开始时间为8，所以写8

9

10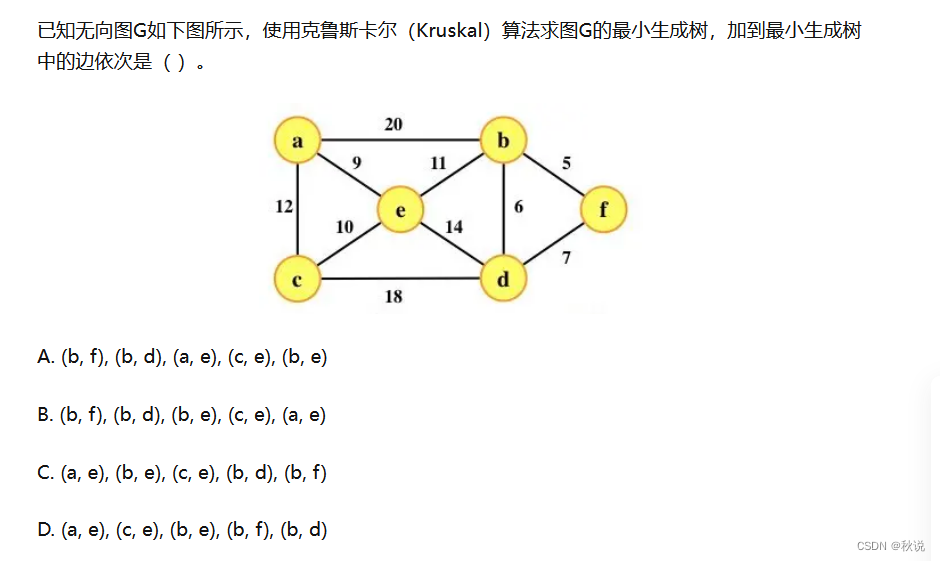

11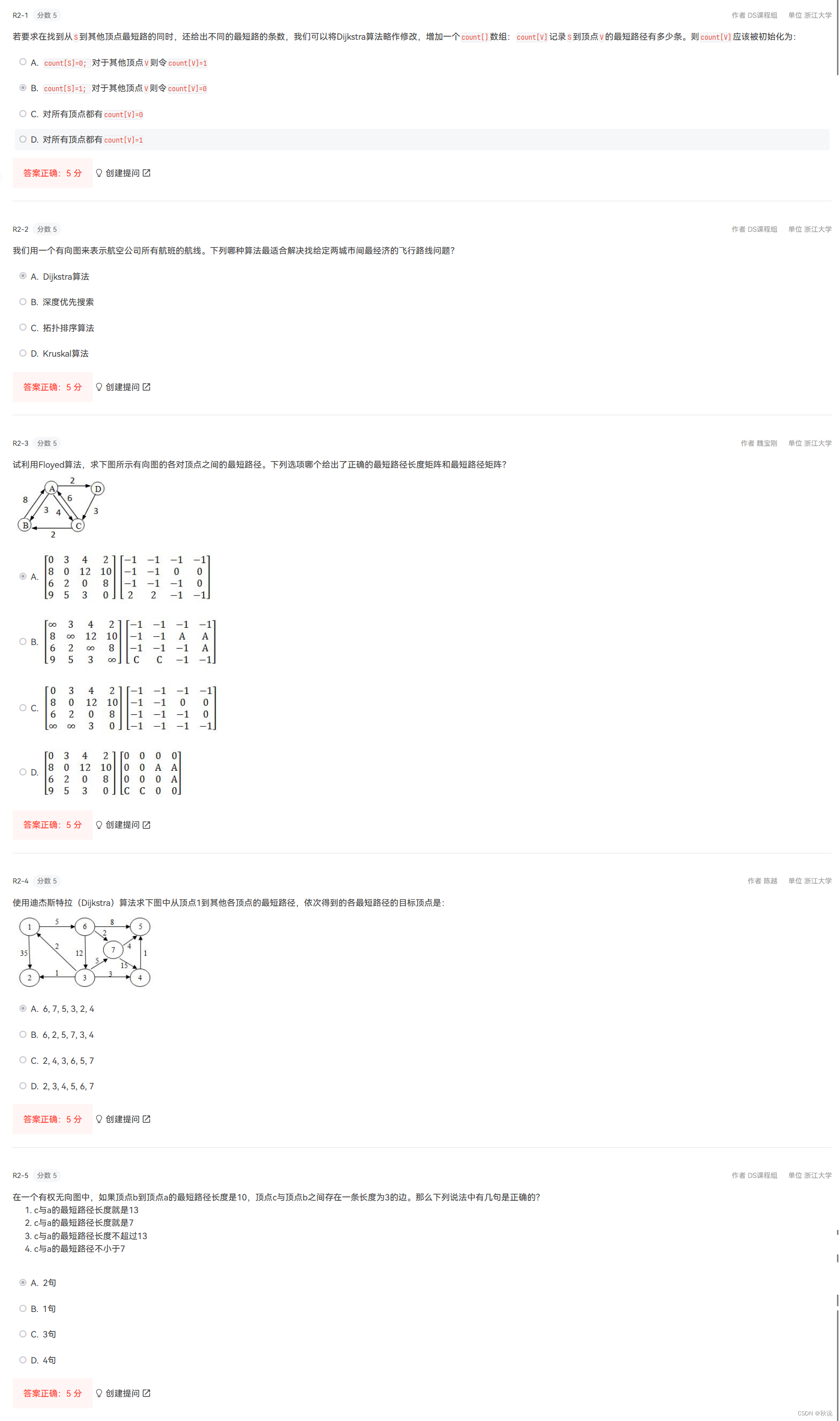
12
13

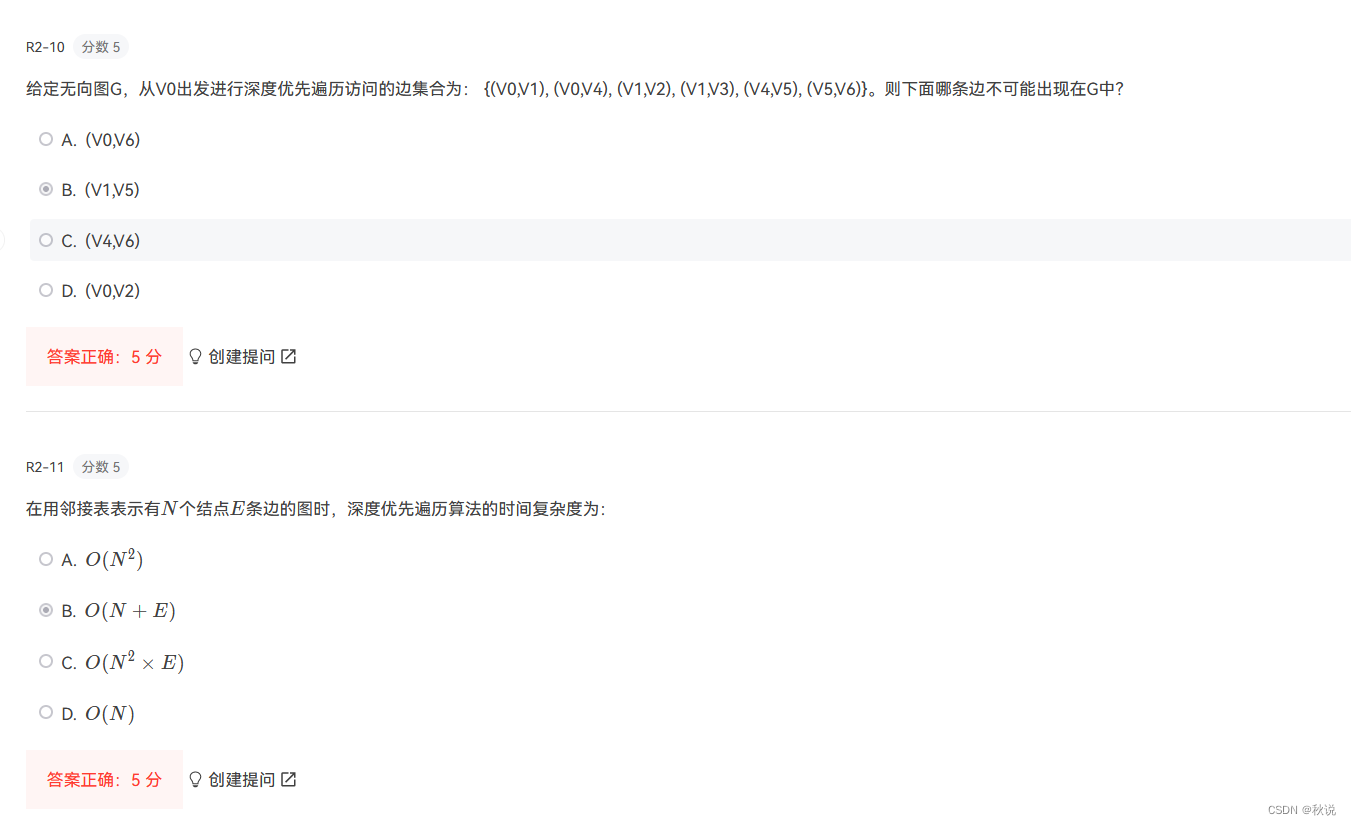
14

6个顶点的无向图最多15条边
3个顶点的无向图最多3条边
6个顶点15条边的图和3个顶点2条边的图以及41个顶点，共计43个连通分量
7个顶点的无向图最多21条边，
7个顶点17条边的图和43个顶点，共计44个连通分量，此时满足最大的要求

15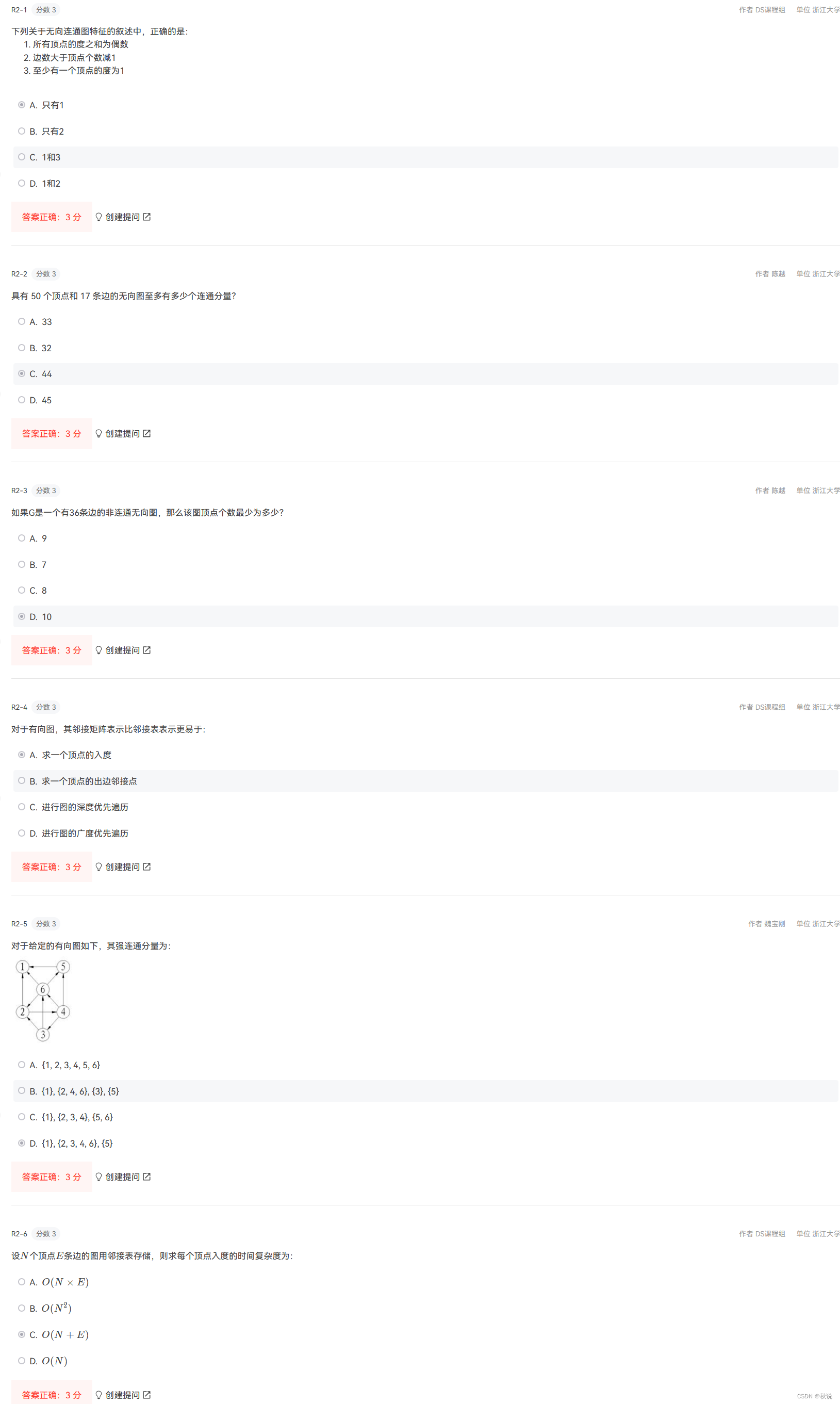
16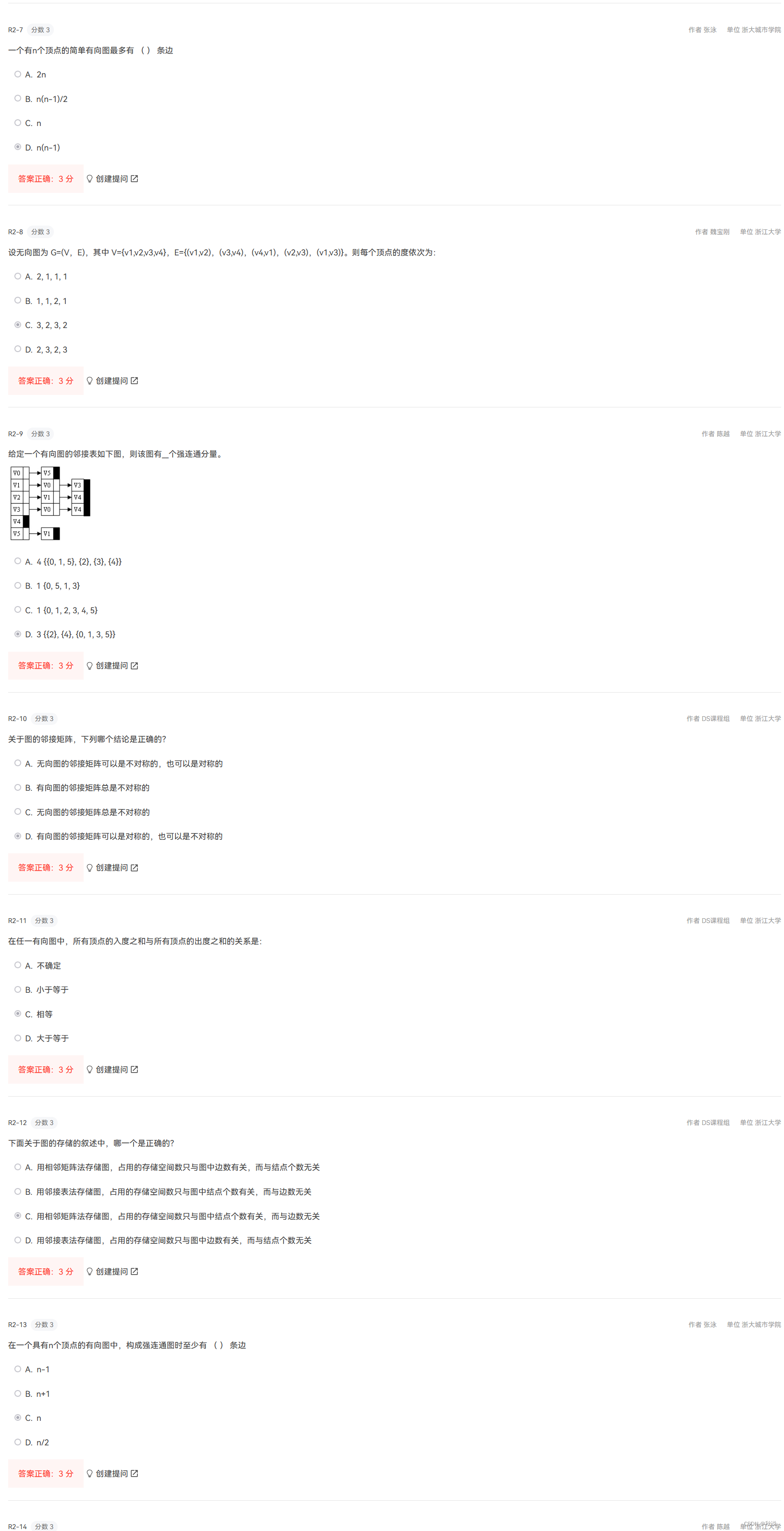

17.具有 100 个顶点和 12 条边的无向图至多有多少个连通分量？（95）

n个顶点的无向图最多有n(n-1)/2条边
n个顶点的无向图最少有n-1条边

而6个顶点最多有15条边
所以
将100个顶点中拿六个顶点构成12条边，形成一个连通分量
此时剩94个点，让它们不相连、各自成为点，所以剩下的94个顶点有94个连通分量，共95个连通分量

编程题

R7-1 社交网络图中结点的“重要性”计算

在社交网络中，个人或单位（结点）之间通过某些关系（边）联系起来。他们受到这些关系的影响，这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用，可以增强也可以减弱。而结点根据其所处的位置不同，其在网络中体现的重要性也不尽相同。

输入样例:

9 14
1 2
1 3
1 4
2 3
3 4
4 5
4 6
5 6
5 7
5 8
6 7
6 8
7 8
7 9
3 3 4 9

输出样例:

Cc(3)=0.47
Cc(4)=0.62
Cc(9)=0.35

#include <bits/stdc++.h>
using namespace std;
const int N = 1010, M = 10010, INF = 1e9;
long long res = 0; // 存储最短路径之和
int n, m, q, x;   // n为顶点数，m为边数，q为查询次数，x为查询的顶点编号
int d[N][N];      // 存储图中每对顶点之间的距离

// Floyd算法求解最短路径
void floyd() {
    for (int k = 1; k <= n; k++) {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
            }
        }
    }
}

int main() {
    cin >> n >> m; // 输入顶点数和边数
    // 初始化距离矩阵
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (i == j)
                d[i][j] = 0;
            else
                d[i][j] = INF;
        }
    }

    // 输入边的信息，更新距离矩阵
    for (int i = 0; i < m; i++) {
        int a, b;
        cin >> a >> b;
        d[a][b] = d[b][a] = 1;
    }

    floyd(); // 求解最短路径

    cin >> q; // 输入查询次数
    bool fg = false;
    for (int i = 0; i < q; i++) {
        res = 0;
        cin >> x; // 输入查询的顶点编号

        // 如果有顶点到其他顶点的最短路径为无穷大，则无法计算Cc(x)，直接输出0.00
        if (!fg) {
            for (int j = 1; j <= n; j++) {
                if (x == j)
                    continue;
                if (d[x][j] > INF / 2) {
                    fg = true;
                    break;
                }
                res += d[x][j];
            }
        }

        if (fg)
            printf("Cc(%d)=0.00\n", x);
        else {
            double ans = (double)(n - 1) / res;
            printf("Cc(%d)=%.2lf\n", x, ans); // 输出结果，保留两位小数
        }
    }
    return 0;
}

R7-2 列出连通集

给定一个有N个顶点和E条边的无向图，请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N?1编号。进行搜索时，假设我们总是从编号最小的顶点出发，按编号递增的顺序访问邻接点。

输入格式:

输入第1行给出2个整数N(0<N≤10)和E，分别是图的顶点数和边数。随后E行，每行给出一条边的两个端点。每行中的数字之间用1空格分隔。

输出格式:

按照"{ v1 v2 … vk }"的格式，每行输出一个连通集。先输出DFS的结果，再输出BFS的结果。

输入样例:

8 6
0 7
0 1
2 0
4 1
2 4
3 5

输出样例:

{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int a[15][15], vis[15];  // 定义邻接矩阵a和访问标记数组vis
int n, e;  // 定义顶点数n和边数e

void DFS(int x)
{
    vis[x] = 1;  // 标记顶点x为已访问
    for (int i = 0; i < n; i++)
    {
        if (a[x][i] == 1 && vis[i] == 0)  // 若顶点i与x相连且未访问过
        {
            printf(" %d", i);  // 输出顶点i
            DFS(i);  // 递归访问顶点i的相邻顶点
        }
    }
}

void BFS(int x)
{
    int q[15];  // 定义队列q用于广度优先搜索
    int front = -1, rear = -1;  // 定义队列的头尾指针
    vis[x] = 1;  // 标记顶点x为已访问
    q[++rear] = x;  // 将顶点x入队
    while (rear > front)
    {
        int t = q[++front];  // 出队一个顶点t
        for (int i = 0; i < n; i++)
        {
            if (a[t][i] == 1 && vis[i] == 0)  // 若顶点i与t相连且未访问过
            {
                printf(" %d", i);  // 输出顶点i
                vis[i] = 1;  // 标记顶点i为已访问
                q[++rear] = i;  // 将顶点i入队
            }
        }
    }
}

int main()
{
    scanf("%d %d", &n, &e);  // 输入顶点数n和边数e
    while (e--)
    {
        int u, v;
        scanf("%d %d", &u, &v);
        a[u][v] = 1;  // 标记顶点u和v之间有边
        a[v][u] = 1;  // 无向图需要将邻接矩阵对称
    }
    memset(vis, 0, sizeof(vis));  // 初始化访问标记数组vis为0
    for (int i = 0; i < n; i++)  // 对每个顶点进行遍历
    {
        if (vis[i] == 0)  // 如果顶点i未被访问过
        {
            printf("{ %d", i);  // 输出当前连通分量的起始顶点i
            DFS(i);  // 对以i为起点的连通分量进行深度优先搜索
            printf(" }\n");
        }
    }
    memset(vis, 0, sizeof(vis));  // 重新初始化访问标记数组vis为0
    for (int i = 0; i < n; i++)  // 对每个顶点进行遍历
    {
        if (vis[i] == 0)  // 如果顶点i未被访问过
        {
            printf("{ %d", i);  // 输出当前连通分量的起始顶点i
            BFS(i);  // 对以i为起点的连通分量进行广度优先搜索
            printf(" }\n");
        }
    }
    return 0;
}

R7-3 分而治之

分而治之，各个击破是兵家常用的策略之一。在战争中，我们希望首先攻下敌方的部分城市，使其剩余的城市变成孤立无援，然后再分头各个击破。为此参谋部提供了若干打击方案。本题就请你编写程序，判断每个方案的可行性。

输入格式：

输入在第一行给出两个正整数 N 和 M（均不超过10 000），分别为敌方城市个数（于是默认城市从 1 到 N 编号）和连接两城市的通路条数。随后 M 行，每行给出一条通路所连接的两个城市的编号，其间以一个空格分隔。在城市信息之后给出参谋部的系列方案，即一个正整数 K （≤ 100）和随后的 K 行方案，每行按以下格式给出：

Np v[1] v[2] ... v[Np]

其中 Np 是该方案中计划攻下的城市数量，后面的系列 v[i] 是计划攻下的城市编号。

输出格式：

对每一套方案，如果可行就输出YES，否则输出NO。

输入样例：

10 11
8 7
6 8
4 5
8 4
8 1
1 2
1 4
9 8
9 1
1 10
2 4
5
4 10 3 8 4
6 6 1 7 5 4 9
3 1 8 4
2 2 8
7 9 8 7 6 5 4 2

输出样例：

NO
YES
YES
NO
NO

#include <bits/stdc++.h>
using namespace std;
vector<int>v[10001];  // 定义图的邻接表表示，v[i]表示与顶点i相邻的所有顶点
int n, m;  // 定义顶点数n和边数m
int book[10001];  // 定义标记数组book，用于标记顶点是否属于给定的顶点集合

bool cmp(int n)
{
    int i, j;
    for (i = 0; i < n; i++)  // 遍历所有顶点
    {
        for (j = 0; j < v[i].size(); j++)  // 遍历与顶点i相邻的所有顶点
        {
            if (!book[i] && !book[v[i][j]])  // 如果顶点i和v[i][j]都不属于给定的顶点集合
                return false;  // 返回false，说明当前顶点集合不是一个连通块
        }
    }
    return true;  // 如果遍历完所有顶点和相邻顶点都符合条件，则返回true，说明当前顶点集合是一个连通块
}

int main()
{
    scanf("%d %d", &n, &m);  // 输入顶点数n和边数m

    int a, b;
    for (int i = 0; i < m; i++)  // 输入每条边，构造邻接表
    {
        scanf("%d %d", &a, &b);
        v[a].push_back(b);
        v[b].push_back(a);
    }

    int k;
    scanf("%d", &k);  // 输入需要判断的顶点集合个数

    for (int i = 0; i < k; i++)  // 遍历每个需要判断的顶点集合
    {
        int np;
        scanf("%d", &np);  // 输入当前顶点集合的大小

        int city;
        memset(book, 0, sizeof(book));  // 初始化标记数组book为0
        for (int j = 0; j < np; j++)  // 输入当前顶点集合中的每个顶点，并标记为1
        {
            scanf("%d", &city);
            book[city] = 1;
        }

        if (cmp(n) == true)  // 判断当前顶点集合是否是一个连通块
            printf("YES\n");
        else
            printf("NO\n");
    }

    return 0;
}

以上就是图的相关练习，在下一篇中我们还会继续对图的编程进行讲解。