C++算法之递归与递推（1）

一、递归（所有递归=>递归搜索树）

---

1.求斐波拉且数列

分析过程

执行是前序遍历，回溯是后序遍历，和栈的思想相同，先进后出

代码实现

#include<iostream>
using namespace std;
int f(int n)
{
    if(n==1) return 1;
    if(n==2) return 2;
    return f(n-1)+f(n-2);
}
int main()
{
    int n;
    cin>>n;
    cout<<f(n)<<endl;
    return 0;
}

---

2.AcWing 92.递归实现指数型枚举

分析过程

首先我们看数据量n=15，由数据范围反推时间复杂度为或，因为从1~n，每个数有两种情况就有种情况，每个方案长度是n，所以时间复杂度为。

其次递归考虑顺序很重要，我们从1~n依次考虑每个数选或不选，记得要考虑每次递归结束和恢复现场。

代码实现

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;
const int N=16;
int n,st[N];//状态，记录每个位置当前的状态，0表示还没考虑，1表示选择，2表示不选择
void dfs(int u)
{
    if(u>n)//我们从1开始递归，然后递归会到下一位，此为结束条件
    {
        for(int i=1;i<=n;i++)
        {
            if(st[i]==1)
             printf("%d ", i);
        }
            printf("\n");
            return;//一个小分支的结束
    }
    //从第一个开始分两种情况进行递归
    //第一个选择
    st[u]=1;
    dfs(u+1);
    st[u+1]=0;//恢复现场
    //第一个不选择
    st[u]=2;
    dfs(u+1);
    st[u+1]=0;//恢复现场
}
int main()
{
    cin>>n;
    
    dfs(1);
    return 0;
}

---

3.AcWing 94.递归实现排列型枚举

分析过程

①依次枚举每个数放哪个位置

②依次枚举每个位置放哪个数

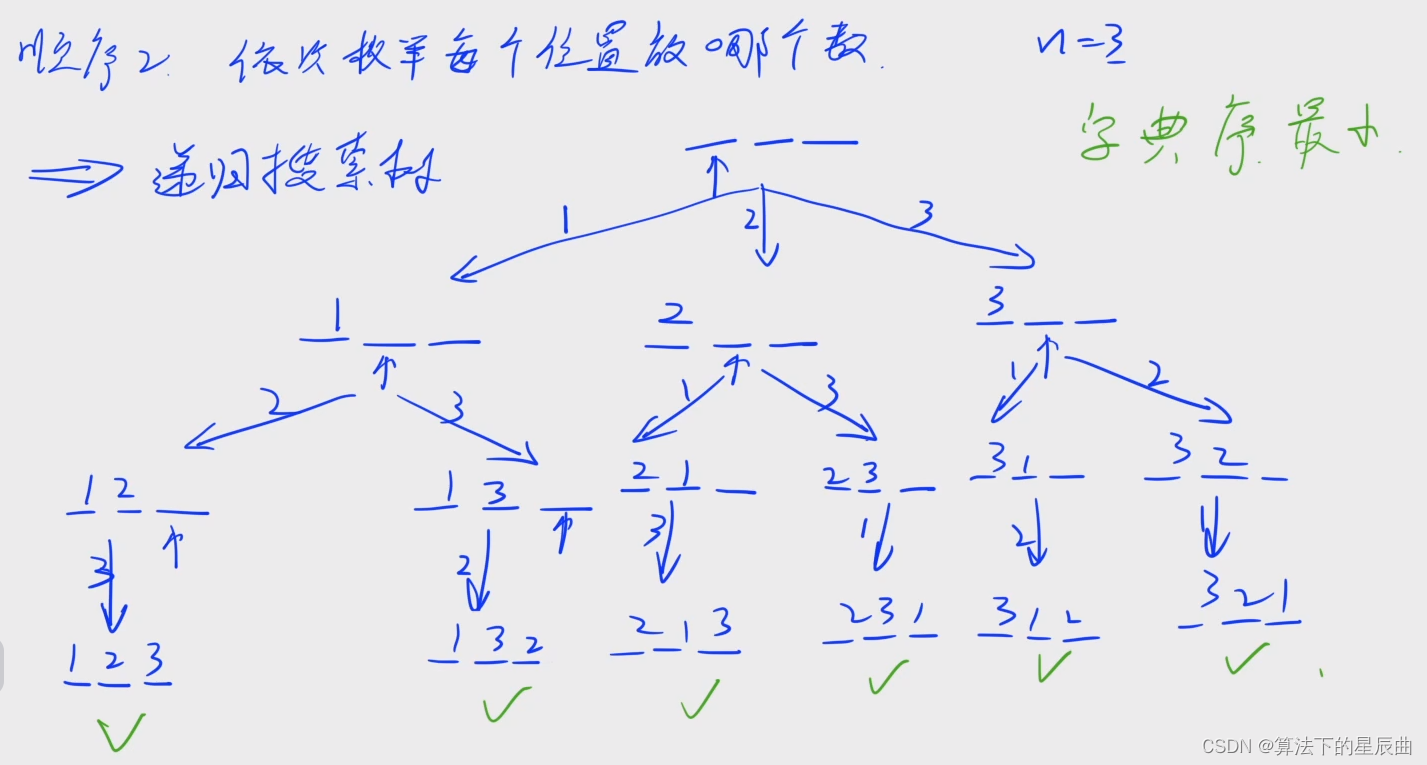
代码实现

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;
const int N=16;
int n,state[N];//0表示未使用，1~n表示放了哪个数
bool used[N];//true表示用过，false表示没有用过
void dfs(int u)
{
    if(u>n)//边界
    {
        for(int i=1;i<=n;i++)
        {
             printf("%d ", state[i]);//打印方案
        }
        cout<<endl;
            return;//一个小分支的结束
    }
    for(int i=1;i<=n;i++)
    {
        if(!used[i])
        {
            state[u]=i;
            used[i]=true;
            dfs(u+1);
            
            //恢复现场
            state[u]=0;
            used[i]=false;
        }
    }
}
int main()
{
    cin>>n;
    
    dfs(1);
    return 0;
}

注：此题也可采用STL知识用next_permutation函数来做

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e8;
int a[N];
int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)a[i] = i;
	do {
		for (int i = 1; i <= n; i++) printf("%d ", a[i]);
		puts("");
	} while (next_permutation(a + 1, a + n + 1));
	return 0;
}

---

4.AcWing 93.递归实现组合型枚举

分析过程

①画出递归搜索树

②搜索数=>代码实现=>dfs(参数)：1）位置 way[N]?2）当前该枚举哪个位置u 3）start 当前应该从哪个数开始枚举

注：此题dfs可优化，采用剪枝的方法，速度可快三倍！

代码实现

#include<iostream>
#include<cstdio>

using namespace std;
const int N=25;
int way[N],n,m;
void dfs(int u,int start)
{
    if(u+n-start<m)return;//剪枝优化
    if(u>m)//结束条件
    {
        for(int i=1;i<=m;i++)printf("%d ",way[i]);
        puts("");
        return;
    }
    for(int i=start;i<=n;i++)
        {
            way[u]=i;
            dfs(u+1,i+1);
            //恢复现场
            way[u]=0;
        }
}

int main()
{
    scanf("%d%d",&n,&m);
    
    dfs(1,1);
    return 0;
}

---

5.AcWing 1209.带分数

分析过程

①枚举a dfs_a

②枚举c dfs_c

③判断b题是否成立

代码实现

#include<bits/stdc++.h>
using namespace std;
const int N=10;
typedef long long LL;
bool st[N],backup[N];
int n;
int ans;
bool check(int a,int c)
{
    LL b=n*(LL)c-a*c;
    if(!a||!b||!c)  return false;
    //拷贝，不影响原有数组
    memcpy(backup,st,sizeof(st));
    //取出b的每一位看是否在a，c种已经出现过
    while(b)
    {
        int x=b%10;//取出个位
        b=b/10;//删除个位
        if(backup[x]||!x) return false;//已经用过或者小于零
        backup[x]=true;
    }
    //再检查是否1~9每位数都已经使用过
    for(int i=1;i<=9;i++)
    {
        if(!backup[i])
        return false;
    }
    return true;
}
void dfs_c(int u,int a,int c)
{
    if(u>9) return;
    //检验等式是否满足
    if(check(a,c)) ans++;
    
    for(int i=1;i<=9;i++)
    {
        if(!st[i])
        {
            st[i]=true;
            dfs_c(u+1,a,c*10+i);
            //恢复现场
            st[i]=false;
        }
    }
}
void dfs_a(int u,int a)
{
    if(a>=n) return;
    if(a) dfs_c(u,a,0);
    
    for(int i=1;i<=9;i++)
    {
        if(!st[i])
        {
            st[i]=true;
            dfs_a(u+1,a*10+i);//将a变成数字的方法
            //还原现场
            st[i]=false;
        }
    }
}
int main()
{
    cin>>n;
    
    dfs_a(0,0);
    
    cout<<ans;
    return 0;
}