《剑指 Offer》专项突破版 - 面试题 8 : 和大于或等于 k 的最短子数组（C++ 实现）- 详解同向双指针（滑动窗口算法）

目录

前言

一、暴力求解

二、同向双指针（滑动窗口算法）

---

?

---

前言

题目链接：. - 力扣（LeetCode）

题目：

输入一个正整数组成的数组和一个正整数 k，请问数组中和大于或等于 k 的连续子数组的最短长度是多少？如果不存在所有数字之和大于或等于 k 的子数组，则返回 0。例如，输入数组 [5, 1, 4, 3]，k 的值为 7，和大于或等于 7 的最短连续子数组是 [4, 3]，因此输出它的长度 2。

分析：

子数组由数组中一个或连续的多个数字组成。一个子数组可以用两个指针表示。如果第 1 个指针 left 指向子数组的第 1 个数字，第 2 个指针 right 指向子数组的最后一个数字，那么子数组就是由这两个指针之间的所有数字组成的。

---

一、暴力求解

最直观的解法就是：

1. 先固定指针 left（最开始指向数组中的第 1 个元素）。

2. 然后从 left 开始不断向右移动指针 right，直到两个指针之间的子数组中所有数字之和大于或等于 k（子数组的长度为 right - left + 1）。

3. 由于目标是找出和大于或等于 k 的最短子数组，要尝试所有的可能，所以 ++left，然后重复步骤 1 和 2，直至不存在和大于或等于 k 的子数组，或 left 超出范围，即 left > n - 1。

   

class Solution {
public:
 ? ?int minSubArrayLen(int target, vector<int>& nums) {
 ? ? ? ?int n = nums.size();
 ? ? ? ?int minLen = n + 1;
 ? ? ? ?for (int left = 0; left < n; ++left)
 ? ? ?  {
 ? ? ? ? ? ?int sum = 0;
 ? ? ? ? ? ?for (int right = left; right < n; ++right)
 ? ? ? ? ?  {
 ? ? ? ? ? ? ? ?sum += nums[right];
 ? ? ? ? ? ? ? ?if (sum >= target)
 ? ? ? ? ? ? ?  {
 ? ? ? ? ? ? ? ? ? ?if (right - left + 1 < minLen)
 ? ? ? ? ? ? ? ? ? ? ? ?minLen = right - left + 1;
 ? ? ? ? ? ? ? ? ? ?
 ? ? ? ? ? ? ? ? ? ?break;
 ? ? ? ? ? ? ?  }
 ? ? ? ? ?  }
 ? ? ? ? ? ?if (sum < target)
 ? ? ? ? ? ? ? ?break;
 ? ? ?  }
 ? ? ? ?return minLen == n + 1 ? 0 : minLen;
 ?  }
};

这种解法的时间复杂度是 O(n^2)。

---

二、同向双指针（滑动窗口算法）

可以对上述解法进行优化。指针 left 和 right 初始化的时候指向数组的第 1 个元素。

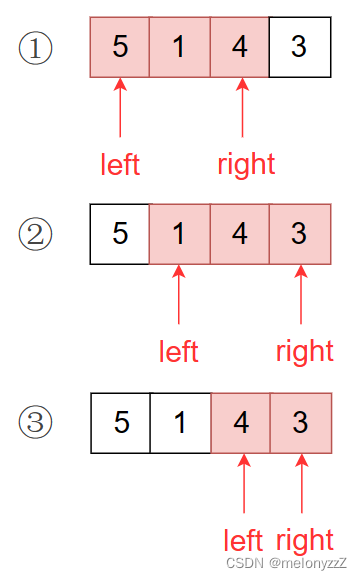
1. 不断向右移动指针 right，直到两个指针之间的子数组数字之和大于或等于 k。

2. 停止右移指针 right，转换不断向右移动指针 left，直到两个指针之间的子数组数字之和小于 k。

   这相当于利用了第 1 步的结果。

3. 重复步骤 2 和 3，直到 right 超出范围，即 right > n - 1。

class Solution {
public:
 ? ?int minSubArrayLen(int target, vector<int>& nums) {
 ? ? ? ?int n = nums.size();
 ? ? ? ?int minLen = n + 1;
 ? ? ? ?int left = 0;
 ? ? ? ?int sum = 0;
 ? ? ? ?for (int right = 0; right < n; ++right)
 ? ? ?  {
 ? ? ? ? ? ?sum += nums[right];
 ? ? ? ? ? ?while (sum >= target)
 ? ? ? ? ?  {
 ? ? ? ? ? ? ? ?if (right - left + 1 < minLen)
 ? ? ? ? ? ? ? ? ? ?minLen = right - left + 1;
 ? ? ? ? ? ? ? ?
 ? ? ? ? ? ? ? ?sum -= nums[left];
 ? ? ? ? ? ? ? ?++left;
 ? ? ? ? ?  }
 ? ? ?  }
 ? ? ? ?return minLen == n + 1 ? 0 : minLen;
 ?  }
};

尽管上述代码中有两个嵌套的循环，该解法的时间复杂度仍然是 O(n)。这是因为在这两个循环中，变量 left 和 right 都是只增加不减少，变量 right 从 0 增加到 n - 1，变量 left 从 0 最多增加到 n - 1，因此总的执行次数是 O(n)。