走迷宫——BFS

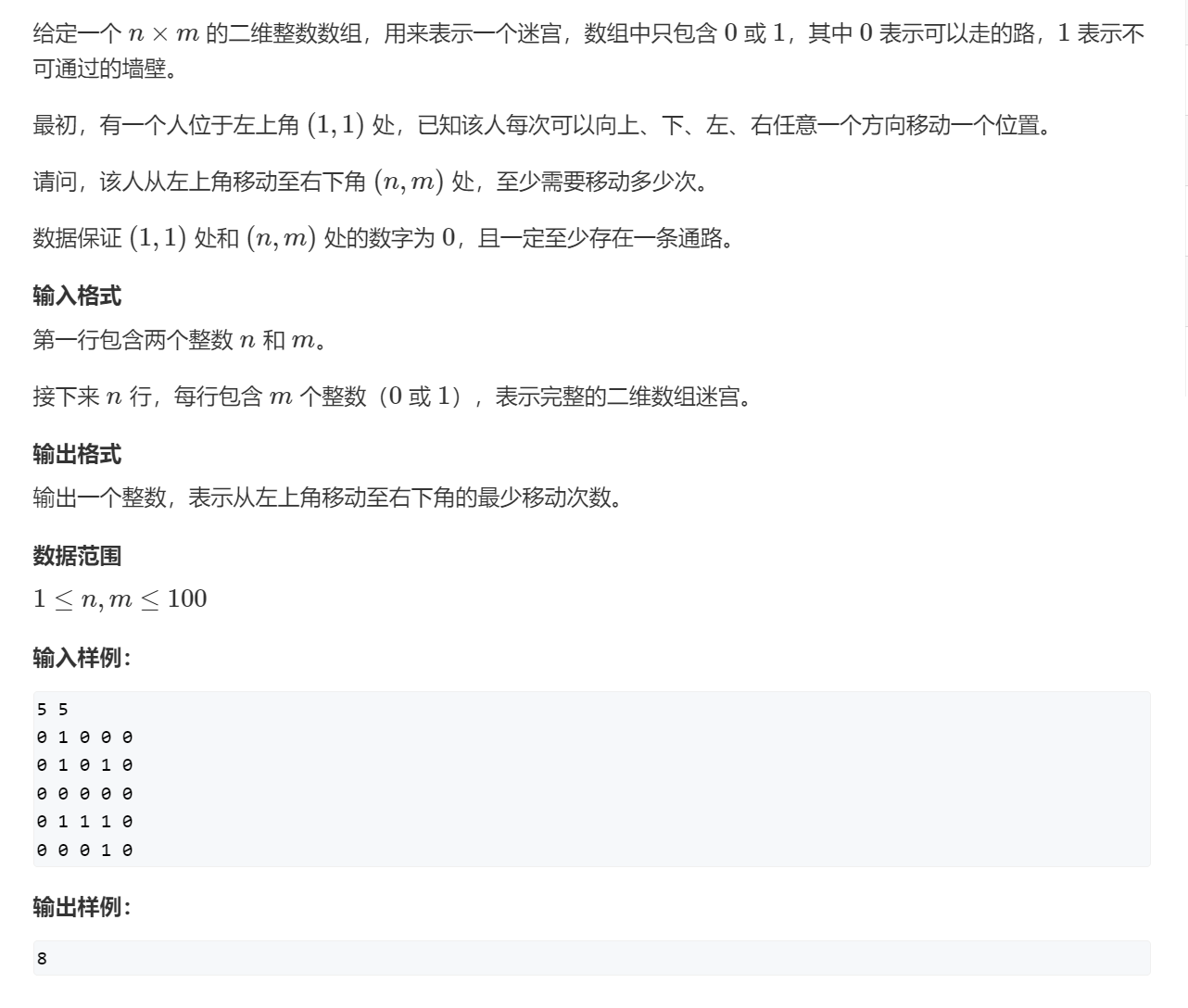
问题描述

思路

• 声明一个队列，存储走过的位置
• 初始化时，将（0， 0）存入队列中
• 每次从队头弹出一个元素，计算从当前元素能走到哪个位置，如果下一个位置符合条件，那么将下一个位置存入队尾中
• 直到队列中没有元素

代码实现

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

const int N = 110;

int n, m;
int d[N][N];	// 表示迷宫，也用来存储走到当前位置的移动次数
PII q[N * N];	// 用数组模拟队列，里面存储的是走过的位置

int bfs()
{
	int hh = 0, tt = 0;	// hh表示队头，tt表示队尾
	q[0] = {0, 0};	// 初始化队列，将（0， 0）存入队列中
	int dx[4] = {-1, 1, 0, 0}, dy[4] = {0, 0, -1, 1};	// 上下左右的偏移量
	while(hh <= tt)		// 队列不为空
	{
		PII t = q[hh++];	// 弹出队头
		for(int i = 0; i < 4; i++)	// 上下左右四个方向移动
		{
			int x = t.first + dx[i], y = t.second + dy[i];	// 从当前位置走到下一个位置
			if(x >= 0 && x < n && y >= 0 && y < m && d[x][y] == 0)	// 下一个位置在棋盘中、没有走过、没有墙壁
			{
				d[x][y] = d[t.first][t.second] + 1;	// 更新下一个位置的移动次数
				q[++tt] = {x, y};	// 将符合条件的下一个位置加入队尾中
			}
		}
	}
	
	return d[n-1][m-1];	// 返回走到（n-1， m-1）这个位置的移动次数
}

int main()
{
	cin >> n >> m;
	for(int i = 0; i < n; i++)
		for(int j = 0; j < m; j++) cin >> d[i][j];
	cout << bfs() << endl;
	
	return 0;
}