Trie 字典树(c++)（前缀）

题目链接：用户登录

题目：

样例：

5 3
aaa
aba
aabbaa
abbbbb
cdd
aabba
abc
abab

Y
N
N

思路：

? ? ? ? 根据题目意思，要用到 Trie 字典树算法。

Trie 字典树，顾名思义，“字典”，我们查字典的时候，都是找开头的几个字符，来获取我们的整个字符，Trie 字典树，就是通过 前缀字符的一步步扩展。最后查找的时候就是根据我们扩展字典树的步骤来变相查找。字典树，我们也要建立一个 root 跟

比如 ：给出以下的几个字符

abcdf

bgre

abfr

baef

最后获得的字典树为：

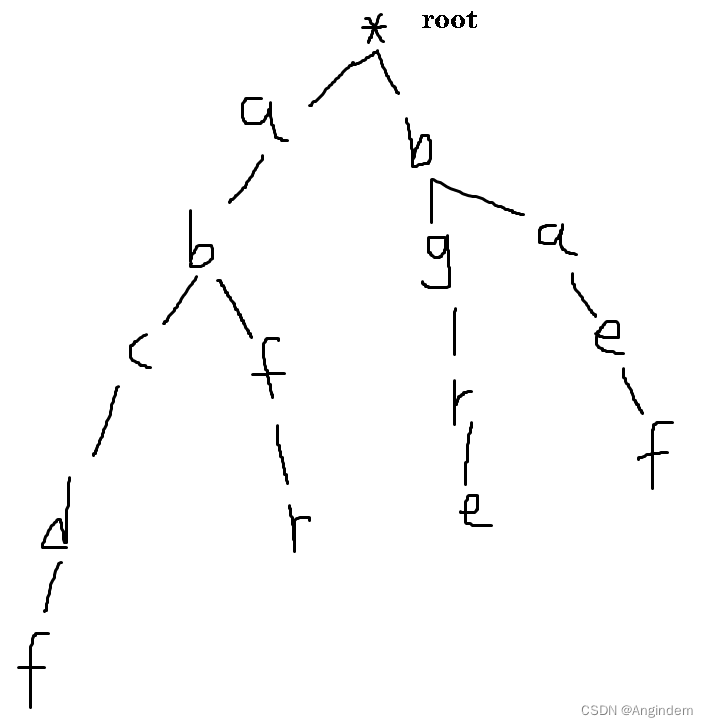
下面给出 Trie 字典树封装的结构体：

// 定义 Tries 结构体，封装
struct Tries
{
	// son 用于存储 字符，idx 对应映射整数地址
	int son[N][26],idx;
	
	// 构造 Tries 初始化
	inline Tries()
	{
		memset(son,0,sizeof son);
		idx = 0;
	}
	
	// 字符串 插入操作
	inline void Insert(string str)
	{
		int p = 0;	// 对应root根树的 映射地址
		int len = str.size();	// 计算 字符串 的长度，方便遍历
		for(int i = 0;i < len;++i)
		{
			int u = str[i] - 'a';	// 将 单个字符 转化为 映射整数地址
			if(!son[p][u]) son[p][u] = ++idx;	// 如果没有当前 地址，扩展映射
			p = son[p][u];	// 往 存在的结点地址 开始下一次检索
		}
		return ;
	}
	
	// 字符串 查找操作 和 插入操作相似，只是不会新建结点
	inline bool query(string str)
	{
		int p = 0;	// 对应root根树的 映射地址
		int len = str.size();	// 计算 字符串 的长度，方便遍历
		for(int i = 0;i < len;++i)
		{
			int u = str[i] - 'a';	// 将 单个字符 转化为 映射整数地址
			if(!son[p][u]) return false;	// 如果没有当前 地址，扩展映射
			p = son[p][u];	// 往 存在的结点地址 开始下一次检索
		}
		return true;
	}
}tree;

代码详解如下：

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#define endl '\n'
#define int long long
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;

// 定义 Tries 结构体，封装
struct Tries
{
	// son 用于存储 字符，idx 对应映射整数地址
	int son[N][26],idx;
	
	// 构造 Tries 初始化
	inline Tries()
	{
		memset(son,0,sizeof son);
		idx = 0;
	}
	
	// 字符串 插入操作
	inline void Insert(string str)
	{
		int p = 0;	// 对应root根树的 映射地址
		int len = str.size();	// 计算 字符串 的长度，方便遍历
		for(int i = 0;i < len;++i)
		{
			int u = str[i] - 'a';	// 将 单个字符 转化为 映射整数地址
			if(!son[p][u]) son[p][u] = ++idx;	// 如果没有当前 地址，扩展映射
			p = son[p][u];	// 往 存在的结点地址 开始下一次检索
		}
		return ;
	}
	
	// 字符串 查找操作 和 插入操作相似，只是不会新建结点
	inline bool query(string str)
	{
		int p = 0;	// 对应root根树的 映射地址
		int len = str.size();	// 计算 字符串 的长度，方便遍历
		for(int i = 0;i < len;++i)
		{
			int u = str[i] - 'a';	// 将 单个字符 转化为 映射整数地址
			if(!son[p][u]) return false;	// 如果没有当前 地址，扩展映射
			p = son[p][u];	// 往 存在的结点地址 开始下一次检索
		}
		return true;
	}
}tree;
int n,k;
string s;
inline void solve()
{
	cin >> n >> k;
	while(n--)
	{
		cin >> s;
		tree.Insert(s);
	}
	while(k--)
	{
		cin >> s;
		if(tree.query(s)) cout << "Y" << endl;
		else cout << "N" << endl;
	}
}

signed main()
{
//	freopen("a.txt", "r", stdin);
	IOS;
	int _t = 1;
//	cin >> _t;
	while (_t--)
	{
		solve();
	}

	return 0;
}

最后提交：