Open CASCADE学习|向量运算

目录

1、计算向量的模

2、计算向量的平方模

3、计算叉乘

4、向量三重积

5、计算点乘

6、标量三重积

---

gp_XYZ.hxx文件定义了gp_XYZ类，该类有3个私有变量：

Standard_Real x;
Standard_Real y;
Standard_Real z;

1、计算向量的模

//! computes Sqrt (X*X + Y*Y + Z*Z) where X, Y and Z are the three coordinates of this XYZ object.
Standard_Real Modulus() const { return sqrt (x * x + y * y + z * z); }

2、计算向量的平方模

//! Computes X*X + Y*Y + Z*Z where X, Y and Z are the three coordinates of this XYZ object.
Standard_Real SquareModulus() const { return (x * x + y * y + z * z); }

3、计算叉乘

//! @code
//! <me>.X() = <me>.Y() * theOther.Z() - <me>.Z() * theOther.Y()
//! <me>.Y() = <me>.Z() * theOther.X() - <me>.X() * theOther.Z()
//! <me>.Z() = <me>.X() * theOther.Y() - <me>.Y() * theOther.X()
//! @endcode
void Cross (const gp_XYZ& theOther);
//=======================================================================
//function : Cross
// purpose :
//=======================================================================
inline void gp_XYZ::Cross (const gp_XYZ& theRight)
{
  Standard_Real aXresult = y * theRight.z - z * theRight.y;
  Standard_Real aYresult = z * theRight.x - x * theRight.z;
  z = x * theRight.y - y * theRight.x;
  x = aXresult;
  y = aYresult;
}

4、向量三重积

向量三重积是三个向量中的一个和另两个向量的叉积相乘得到的叉积，其结果是个向量。

假如a，b，c线性独立（不共面），首先a×(b×c)必然落在b和c张成的平面上。因为b×c垂直于b和c，而a×(b×c)垂直于b×c，所以在三维空间中，必然落于b和c张成的平面上。那么a×(b×c)就可以写成b和c的线性组合。

  //! Triple vector product
  //! Computes <me> = <me>.Cross(theCoord1.Cross(theCoord2))
  void CrossCross (const gp_XYZ& theCoord1, const gp_XYZ& theCoord2);

  //! Triple vector product
  //! computes New = <me>.Cross(theCoord1.Cross(theCoord2))
  Standard_NODISCARD gp_XYZ CrossCrossed (const gp_XYZ& theCoord1, const gp_XYZ& theCoord2) const
  {
    gp_XYZ aCoord0 = *this;
    aCoord0.CrossCross (theCoord1, theCoord2);
    return aCoord0;
  }
//=======================================================================
//function : CrossCross
// purpose :
//=======================================================================
inline void gp_XYZ::CrossCross (const gp_XYZ& theCoord1, const gp_XYZ& theCoord2)
{
  Standard_Real aXresult = y * (theCoord1.x * theCoord2.y - theCoord1.y * theCoord2.x) -
                           z * (theCoord1.z * theCoord2.x - theCoord1.x * theCoord2.z);
  Standard_Real anYresult = z * (theCoord1.y * theCoord2.z - theCoord1.z * theCoord2.y) -
                            x * (theCoord1.x * theCoord2.y - theCoord1.y * theCoord2.x);
  z = x * (theCoord1.z * theCoord2.x - theCoord1.x * theCoord2.z) -
      y * (theCoord1.y * theCoord2.z - theCoord1.z * theCoord2.y);
  x = aXresult;
  y = anYresult;
}

这里的计算方法为：Coord =Coord×（theCoord1×theCoord2）

5、计算点乘

//! computes the scalar product between <me> and theOther
 Standard_Real Dot (const gp_XYZ& theOther) const { return(x * theOther.x + y * theOther.y + z * theOther.z); }

6、标量三重积

设已知三个向量a、b和c.如果先作两向量?a和b的向量积a×b，把所得到的向量与第三个向量?c再作数量积（a×b）·c，这样得到的数量叫做三向量a、b、c?的标量三重积，记作[abc].

标量三重积的数值等于以a、b、c为相邻3条棱边的平行6面体的体积。

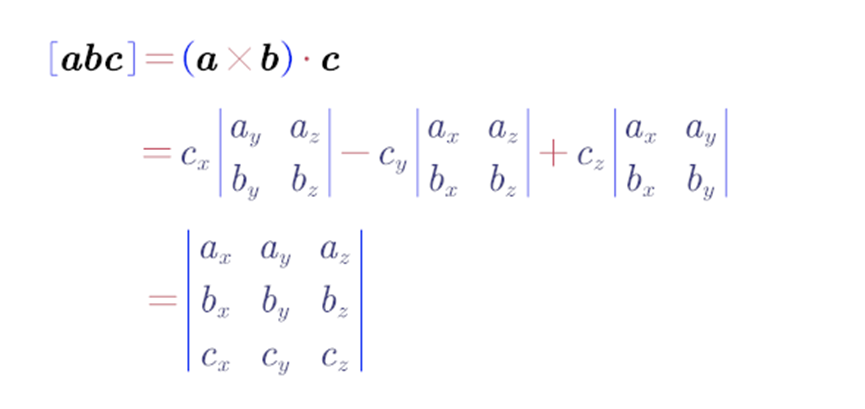
//! computes the triple scalar product
Standard_Real DotCross (const gp_XYZ& theCoord1, const gp_XYZ& theCoord2) const;
//=======================================================================
//function : DotCross
// purpose :
//=======================================================================
inline Standard_Real gp_XYZ::DotCross (const gp_XYZ& theCoord1, const gp_XYZ& theCoord2) const
{
  Standard_Real aXresult = theCoord1.y * theCoord2.z - theCoord1.z * theCoord2.y;
  Standard_Real anYresult = theCoord1.z * theCoord2.x - theCoord1.x * theCoord2.z;
  Standard_Real aZresult = theCoord1.x * theCoord2.y - theCoord1.y * theCoord2.x;
  return (x * aXresult + y * anYresult + z * aZresult);
}

这里的计算方法为：Coord =Coord·（theCoord1×theCoord2）