Python 手搓神经网络——BP反向传播

发布时间：2023年12月28日

摆烂…先写这么多，有空来更新（指的是矩阵求导部分懒得写现在）

本打算围绕《Learning representations by back-propagating errors》一文进行解读的

奈何没有中文版的文档（~~笔者懒得翻译 English~~）

所以文章内容只能根据笔者自身对 BP 反向传播算法的理解来编写咯~😅

在论文的标题里写道back-propagating errors，即反向传播误差

先通过前向传播计算得到输出结果（预测值）
进而计算输出结果与正确值之间的误差
将误差反向传播，并更新参数，得以实现“学习”的目的
至于…误差如何反向传播，参数如何得以更新，也是本文在探讨的

import random
import numpy as np
import tensorflow as tf
from matplotlib import pyplot as plt

定义激活函数、损失函数

这里只采用 ReLU、Sigmoid 作为神经网络的激活函数，MSE 作为损失函数

下面列了这仨的计算公式与导数的计算公式。除了定义计算公式，也定义了其求导公式，因为链式法则，懂吧？😁 就是为了方便后面的求导（也就是误差反向传播）

ReLU

$R e LU = ma x (0, x)$
$\frac{\mathrm{d} y}{\mathrm{d} x} = \left\{\begin{matrix} 1 \quad ,x > 0\\ 0 \quad ,x \le 0 \end{matrix}\right.$

Sigmoid

$Sigmoid=\frac{1}{1+e^{-x}}$
$\frac{\mathrm{d} y}{\mathrm{d} x} = x\cdot (1-x)$

MSE

$MSE=\frac{1}{n}\sum (pred-true)^{2}$
$\frac{\mathrm{d} y}{\mathrm{d} x} = pred-true$

# ReLU 激活函数
class ReLU:
    def __call__(self, x):
        return np.maximum(0, x)
    # 对 ReLU 求导
    def diff(self, x):
        x_temp = x.copy()
        x_temp[x_temp > 0] = 1
        return x_temp

# Sigmoid 激活函数
class Sigmoid:
    def __call__(self, x):
        return 1/(1+np.exp(-x))
    # 对 Sigmoid 求导
    def diff(self, x):
        return x*(1-x)

# MSE 损失函数
class MSE:
    def __call__(self, true, pred):
        return np.mean(np.power(pred-true, 2), keepdims=True)
    # 对 MSE 求导
    def diff(self, true, pred):
        return pred-true

relu = ReLU()
sigmoid = Sigmoid()
mse = MSE()

简单的 BP 反向传播

这里从最简单的开始，隐藏层只设置一个神经元，用sigmoid作为激活函数

一切随缘🔀，对于x、w、b、true全都随机生成。而这一个神经元的任务就是不断的卷（学习），让输出结果无限接进true

整个神经网络的模型图如下，将就着看吧，笔者懒得弄图😅😅😅

|————————————输入层
|   |————————隐藏层
|   |   |————输出层
〇——〇——〇

前向计算过程：x -> w·x+b -> sigmoid(w·x+b) -> mse(true, sigmoid(w·x+b))

反向计算过程：
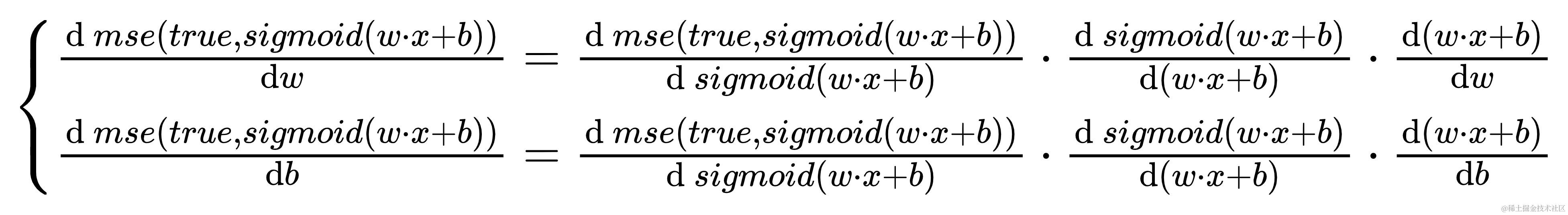
手搓神经网络——BP反向传播-1.jpg

天地！反向计算得过程好复杂哇🙀。但一句概括得话就是误差对参数求导，这里就是在用链式法则对w与b求导，仅此而已

而更新得计算方式就是，参数自身减去lr乘?误差对参数的求导结果
$\left\{\begin{matrix} w = w-lr\cdot \frac{\mathrm{d}\ mse(true, sigmoid(w·x+b))}{\mathrm{d}w} \\ b = b-lr\cdot \frac{\mathrm{d}\ mse(true, sigmoid(w·x+b))}{\mathrm{d}b} \\ \end{matrix}\right.$

约法 6 章：

x：输入的值
w：权重
b：偏置
true：我们要的正确值
lr：学习率
epochs：学习次数

x = random.random()
w = random.random()
b = random.random()
true = random.random()
print(f'x={x}   true={true}')

lr = 0.3
epochs = 520
# 用于记录 loss
loss_hisory = []
for epoch in range(epochs):
    # 获取预测值
    pred = sigmoid(w * x + b)
    # 计算损失
    loss = mse(true, pred)
    # 更新参数
    w -= lr * x * sigmoid.diff(pred) * mse.diff(true, pred)
    b -= lr * sigmoid.diff(pred) * mse.diff(true, pred)
    if epoch % 100 == 0:
        print(f'epoch {epoch}, loss={loss}, pred={pred}')
    loss_hisory.append(loss)

print(f'epoch {epoch+1}, loss={loss}, pred={pred}')
# 绘制 loss 曲线图
plt.plot(loss_hisory)
plt.show()
==============================
输出：
x=0.11313136923799194 true=0.8484027350076178
epoch 0, loss=0.017935159490587653, pred=0.7144805206793456
epoch 100, loss=0.0025295950301247104, pred=0.7981076554259657
epoch 200, loss=0.000615626922003235, pred=0.8235909047243993
epoch 300, loss=0.00018266148479303084, pred=0.8348875034227343
epoch 400, loss=5.94620257403187e-05, pred=0.8406915725958721
epoch 500, loss=2.0323334362411495e-05, pred=0.8438945941089311
epoch 520, loss=1.6631758505966922e-05, pred=0.8443245297030791

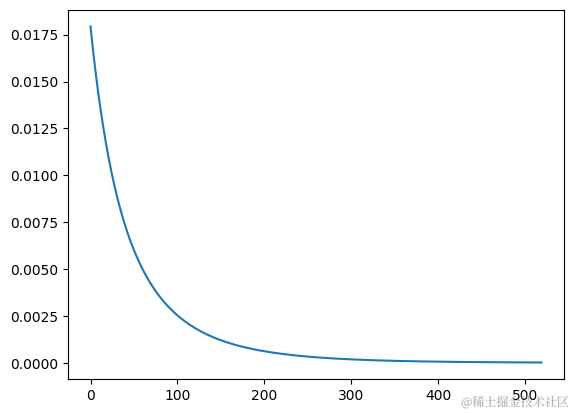
loss 图中的曲线也是呈下降的趋势，输出的预测值pred是在不断的接近true的，说明确确实实起到了“学习”的效果。下面来瞅瞅为啥要求导吧

# 假设有一批预测值 pred
pred = np.arange(-20, 21)
true = 1

# MSE 的曲线图
plt.plot((pred-true)**2, label='MSE')
plt.scatter(21, 1, color='red', label='true')
plt.scatter(30, 81, color='orange', label='pred 1')
plt.scatter(12, 81, color='green', label='pred 2')
plt.plot(np.arange(25, 40), 2*9*(np.arange(15))-10, label='line 1(k=18)')
plt.plot(np.arange(5, 20), 2*-9*(np.arange(15))+205, label='line 2(k=-18)')
plt.legend()
plt.show()

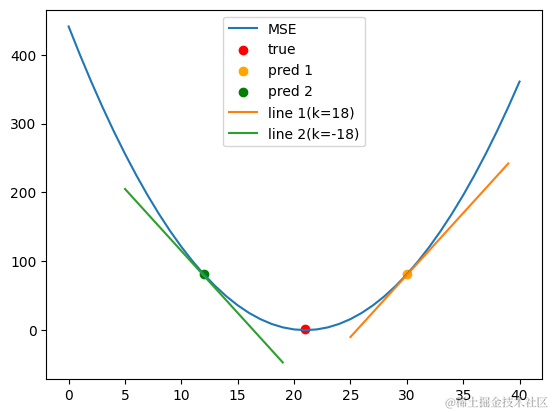
上面是一张MSE的曲线图

红点🔴是true，是我们想要的预期值，在这个点的时候误差最小
橙点🟠是pred，也是神经网络的输出值
橙色的线条是在于MSE曲线上橙点🟠处的切线（这条线的斜率为18）
绿色的线条是在于MSE曲线上绿点🟢处的切线（这条线的斜率为-18）

那么…有趣的来了，对于橙点🟠，误差要向左减小。对于绿点🟢，误差要向右减小。观察两条切线的斜率，这能发现这与斜率的方向（正负）有关系

至此，笔者认为：计算误差对参数（权重w and 偏置b）的导数，根据其导数的正负即可得出参数更新的方向（是加? or 是减🗡?）

从而得到参数更新的计算方式，参数自身减去lr乘?误差对参数的求导结果
$\left\{\begin{matrix} w = w-lr\cdot \frac{\mathrm{d}\ loss}{\mathrm{d}w} \\ b = b-lr\cdot \frac{\mathrm{d}\ loss}{\mathrm{d}b} \\ \end{matrix}\right.$

那学习率lr还有什么用，lr能控制学习的速度。但太小会导致学的慢，太大会导致难以收敛（用上面的MSE曲线图来解释的话，就是原本在橙点🟠处，结果学习率太大，一学学过头跳到绿点🟢所在的地方了）

高级的 BP 反向传播

前面只是开胃菜🍅🍆🥔🥕🫑🫛，这里难度加加加！使用矩阵的方式，再实现一次

与前面神经网络不同的是，这次的隐藏层含有3个神经元。输入x仍然是随缘，只不过我们要的正确值true在这里指定为[0.1]

有亿点长，但笔者认为不复杂

前向计算过程：x -> x@w1+b1 -> sigmoid(x@w1+b1) -> sigmoid(x@w1+b1)@w2+b2 -> sigmoid(sigmoid(x@w1+b1)@w2+b2) -> mse(true, sigmoid(sigmoid(x@w1+b1)@w2+b2))

@是矩阵点乘，注意哦噢😮，因为是已经是矩阵计算了，变成了x@w+b而非之前的w·x+b

整个神经网络的模型图如下

|————————————输入层
|   〇———————隐藏层
|  /  \ |————输出层
〇——〇——〇
   \  /
    〇

x = np.random.rand(1, 1)
# 生成 3 个神经元的权重
w1 = np.random.rand(1, 3)
# 生成 3 个神经元的偏置
b1 = np.random.rand(1, 3)

# 这是输出层的
w2 = np.random.rand(3, 1)
b2 = np.random.rand(1, 1)

# 我们期望得到的正确值
true = np.array([[0.1]])

lr = 0.1
epochs = 520
loss_hisory = []
for epoch in range(epochs):
    # 注意了！?? y是隐藏层的输出 pred是输出层的输出
    y = sigmoid(x@w1+b1)
    pred = sigmoid(y@w2+b2)
    # 计算损失
    loss = mse(true, pred)

    # 时代变了，大人！这里要反着来（先输出层后隐藏层），要不然你以为为什么叫误差反向传播呢？
    # 更新 输出层 参数
    w2 -= lr * x.T @ sigmoid.diff(pred) * mse.diff(true, pred)
    b2 -= lr * sigmoid.diff(pred) * mse.diff(true, pred)
    # 更新 隐藏层 参数
    w1 -= lr * x.T @ (sigmoid.diff(y) * ((sigmoid.diff(pred) * mse.diff(true, pred)) @ w2.T))
    b1 -= lr * (sigmoid.diff(y) * ((sigmoid.diff(pred) * mse.diff(true, pred)) @ w2.T))

    if epoch % 100 == 0:
        print(f'epoch {epoch}, loss={loss}, pred={pred}')
    loss_hisory.append(loss[0])

print(f'epoch {epoch + 1}, loss={mse(true, pred)}, pred={pred}')
# 绘制 loss 曲线图
plt.plot(loss_hisory)
plt.show()
==============================
输出：
epoch 0, loss=[[0.65487189]], pred=[[0.90924155]]
epoch 100, loss=[[0.08011342]], pred=[[0.38304315]]
epoch 200, loss=[[0.00990116]], pred=[[0.19950457]]
epoch 300, loss=[[0.00304457]], pred=[[0.1551776]]
epoch 400, loss=[[0.00126247]], pred=[[0.13553131]]
epoch 500, loss=[[0.00060302]], pred=[[0.12455654]]
epoch 520, loss=[[0.00052945]], pred=[[0.12300987]]

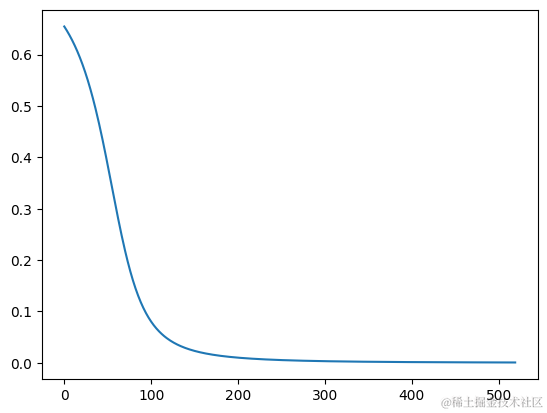
观察输出的pred，非常的nice👋，最后一次的[[0.90332459 0.89611935 0.11057356]]已经足够接近[[1, 1, 0]]了，下面来谈谈重点

这是简单的BP反向传播中的参数更新算法

w -= lr * x * sigmoid.diff(pred) * mse.diff(true, pred)
b -= lr * sigmoid.diff(pred) * mse.diff(true, pred)

这是高级的BP反向传播中的参数更新算法

w -= lr * x.T @ sigmoid.diff(pred) * mse.diff(true, pred)
b -= lr * sigmoid.diff(pred) * mse.diff(true, pred)

观察输出的pred，非常的nice👋，最后一次的[[0.90332459 0.89611935 0.11057356]]已经足够接近[[1, 1, 0]]了，下面来谈谈重点

这是简单的BP反向传播中的参数更新算法

w2 -= lr * x.T @ sigmoid.diff(pred) * mse.diff(true, pred)
b2 -= lr * sigmoid.diff(pred) * mse.diff(true, pred)

这是高级的BP反向传播中的参数更新算法

w -= lr * x.T @ sigmoid.diff(pred) * mse.diff(true, pred)
b -= lr * sigmoid.diff(pred) * mse.diff(true, pred)

都是用链式法则的原理进行损失对参数的求导，从而更新参数。来对比一下，不同之处就在于权重w的更新上了，一个是x * sigmoid.diff(pred)一个则是x.T @ sigmoid.diff(pred)。无非是从x *改成了x.T @（吐槽🤬：娘希匹，就改这么一丢丢，可要笔者老命咯~，要不然这篇文章在3年前就该写出的）

哇趣😭😭😭，对不住了各位。在矩阵求导里为什么用x.T @，笔者也无法解释，只能说这非常重要特别是那个.T和@（其实就是笔者菜🍋🫑🐠）。至于为啥解释不了，请看VCR📽?。y1与y2的区别就是有无激活函数，笔者没搞懂为什么这里的有无对最后的求导计算影响蛮大的

x = tf.constant([[0.5]], dtype='float32')
w = tf.constant([[1, 2, 3]], dtype='float32')
b = tf.constant([[4, 5, 6]], dtype='float32')

with tf.GradientTape() as tape_1, tf.GradientTape() as tape_2:
    tape_1.watch(w)
    tape_2.watch(w)
    y1 = x@w+b
    y2 = tf.nn.sigmoid(x@w+b)

# 使用 tensorflow 求导
print('使用 tensorflow 求导')
diff_1 = tape_1.gradient(y1, w)
diff_2 = tape_2.gradient(y2, w)
print('d(y1)_d(w):', diff_1.numpy())
print('d(y2)_d(w):', diff_2.numpy())
# 使用 numpy 手搓求导
print('\n使用 numpy 手搓求导')
print('d(y1)_d(w):', x.numpy().T)
print('d(y2)_d(w):', x.numpy().T @ sigmoid.diff(y2.numpy()))
==============================
输出：
使用 tensorflow 求导
d(y1)_d(w): [[0.5 0.5 0.5]]
d(y2)_d(w): [[0.00543311 0.00123326 0.00027623]]

使用 numpy 手搓求导
d(y1)_d(w): [[0.5]]
d(y2)_d(w): [[0.00543311 0.00123326 0.00027623]]

对比使用 tensorflow 求导与使用 numpy 手搓求导的d(y1)_d(w)，数值上是对了，但形状不一样。一旦加上了激活函数两者却又一样了，等大佬解释🙏🙏🙏

手搓神经网络

至此，重头戏来咯~🤯🤯🤯，要实现矩阵求导+自动求导，搓出个神经网络 🚀

绷不住啦！笔者必须要吐槽下😡💢😠👿🤬（下面内容与机器学习无关，纯纯笔者吐槽编编写文章时所遇问题，可跳过）

在代码中，NetWork中的self.layers是为了便于记录神经网络层而存在的
if self not in parent.layers:
   parent.layers.append(self)
这段的作用是将Linear层加入到self.layers中，方便后期的反向传播计算。但如果没有if self not in parent.layers:这句，整个神经网络的输入与输出的形>状（shape）就必须一样，否做就会造成矩阵计算错误

Why？在NetWork的fit方法中有pred = self(x)，这是用于前向计算神经网络的输出的，如果没有前面的if语句，就会导致每次调用pred = self(x)时，都会向self.layers中添加Linear层（明明设置了2层的神经网络，第一次调用会添加2层，这是对的，但第二次调用会继续添加2层，导致后期反向传播时造成矩阵计算错误（错误位置new_grad = activation_diff_grad @ self.weight.T））

关于这一点，因为在之前x与true的形状（shape）一直是设置成一样的，所以笔者也没发现

目前读者所读的文章，已经是第 n 个版本了（一直在努力详解内容，与修改勘误中😏😏😏）

# 定义层
class Linear:
    def __init__(self, inputs, outputs, activation):
        '''
        inputs: 输入神经元个数
        outpus: 输出神经元个数
        activation: 激活函数
        '''
        # 初始化 weight
        self.weight = np.random.rand(inputs, outputs)/10
        # 此行是为了防止后期梯度消失而存在的，最简单的方法也可以是 self.weight/10 ，下同
        self.weight = self.weight / self.weight.sum()
        # 初始化 bias
        # 这里只写 outputs 与批大小的计算有关
        self.bias = np.random.rand(outputs)/10
        self.bias = self.bias / self.bias.sum()
        # 激活函数
        self.activation = activation
        # 这里用作后期误差反向传播用
        self.x_temp = None
        self.t_temp = None

    # 层前向计算
    def __call__(self, x, parent):
        self.x_temp = x
        self.t_temp = self.activation(x@self.weight+self.bias)
        # 将此层加入到 layers 当中，便于后期的反向传播操作
        if self not in parent.layers:
            parent.layers.append(self)

        return self.t_temp

    # 更新 weight、bias
    def update(self, grad):
        activation_diff_grad = self.activation.diff(self.t_temp) * grad
        # 这个变量肩负重任，将后面的梯度不断向前传播
        new_grad = activation_diff_grad @ self.weight.T
        # 参数的更新
        self.weight -= lr * self.x_temp.T @ activation_diff_grad
        # 这里的 mean(axis=0) 与批大小的计算有关
        self.bias -= lr * activation_diff_grad.mean(axis=0)
        # 这里将误差继续往前传
        return new_grad

# 定义网络
class NetWork:
    def __init__(self):
        # 储存各层，便于后期的反向传播操作，类似于 tf.keras.Sequential
        self.layers = []
        # 构造神经网络
        self.linear_1 = Linear(4, 16, activation=relu)
        self.linear_2 = Linear(16, 8, activation=relu)
        self.linear_3 = Linear(8, 3, activation=sigmoid)

    # 模型计算
    def __call__(self, x):
        x = self.linear_1(x, self)
        x = self.linear_2(x, self)
        x = self.linear_3(x, self)

        return x

    # 模型训练
    def fit(self, x, y, epochs, step=100):
        for epoch in range(epochs):
            pred = self(x)
            self.backward(y, pred)
            if epoch % step == 0:
                print(f'epoch {epoch}, loss={mse(y, pred)}, pred={pred}')
        print(f'epoch {epoch+1}, loss={mse(y, pred)}, pred={pred}')

    # 反向传播
    def backward(self, true, pred):
        # 对误差求导
        grad = mse.diff(true, pred)
        # 反向更新层参数，反向！！！所以是 reversed，反着更新层
        for layer in reversed(self.layers):
            grad = layer.update(grad)

network = NetWork()

x = np.array([[1, 2, 3, 4]])
true = np.array([[0.1, 0.1, 0.6]])
# 训练 启动！！！
network.fit(x, true, 520, 100)
==============================
输出：
epoch 0, loss=[[0.16011657]], pred=[[0.63736144 0.53769595 0.60382743]]
epoch 100, loss=[[0.01028116]], pred=[[0.22784994 0.21897094 0.61854131]]
epoch 200, loss=[[5.52173933e-05]], pred=[[0.10658826 0.11096641 0.60140883]]
epoch 300, loss=[[1.66720973e-06]], pred=[[0.09978016 0.10222452 0.60006921]]
epoch 400, loss=[[2.65396934e-07]], pred=[[0.09953248 0.10075998 0.60000692]]
epoch 500, loss=[[6.09600151e-08]], pred=[[0.09973331 0.1003343 0.60000093]]
epoch 520, loss=[[4.62963427e-08]], pred=[[0.09976507 0.1002893 0.60000066]]

反正输出显示，pred有在逼近[[0.1, 0.1, 0.6]]，说明模型确确实实是在“学习”的…

TensorFlow 验证

是骡子 🫏 是马 🐎 拉出来溜溜不就晓得了

验证方式

两者皆使用想用的神经网络构造与参数，x与true也相同
用 TensorFlow 计算一次
用手搓的神经网络计算一次
对比loss对层1中w1参数的导数是否一致

神经网络的模型图，如下
手搓神经网络——BP反向传播-1.png

x = tf.random.uniform((1, 2))

# 层 1 的参数
w1 = tf.random.uniform((2, 4))
b1 = tf.random.uniform((4,))
# 层 2 的参数
w2 = tf.random.uniform((4, 8))
b2 = tf.random.uniform((8,))
# 层 3 的参数
w3 = tf.random.uniform((8, 2))
b3 = tf.random.uniform((2,))

true = tf.constant([[0.5, 0.2]])

with tf.GradientTape() as tape_1:
    tape_1.watch(w1)
    # 用 tensoflow 的激活函数前向计算
    y = tf.nn.relu(x@w1+b1)
    y = tf.nn.sigmoid(y@w2+b2)
    y = tf.nn.sigmoid(y@w3+b3)
    # 用 tensoflow 的损失函数计算 loss
    loss = tf.keras.losses.mse(true, y)

print('mse-loss:', loss.numpy())
dLoss_dX = tape_1.gradient(loss, w1)
print('loss 对 w1 的导数:\n', dLoss_dX.numpy())
==============================
输出：
mse-loss: [0.4319956]
loss 对 w1 的导数:
[[0.00111373 0.0012263 0.00095062 0.00114191] [0.00020771 0.0002287 0.00017729 0.00021296]]

因为只是对比计算的结果，这里手搓的神经网络就简化一下子了

重点🚨！！！ 标记处是和获loss对w1的导数有关的
注意了??！ 标记处是细节，为了与tensorflow的结果做对比与上面的手搓神经网络有区别的地方

class Linear:
    def __init__(self, weight, bias, activation):
        # 这里权重、参数不随机生成了，直接用上面 tensorflow 的
        self.weight = weight
        self.bias = bias
        self.activation = activation
        self.x_temp = None
        self.t_temp = None
        # 重点🚨！！！ 为了方便计算 linear_1 里 loss 对 w1 的导数，这个变量用来记录梯度
        self.activation_diff_grad = None

    def __call__(self, x, parent):
        self.x_temp = x 
        self.t_temp = self.activation(x@self.weight+self.bias)
        if self not in parent.layers:
            parent.layers.append(self)

        return self.t_temp

    def update(self, grad):
        self.activation_diff_grad = self.activation.diff(self.t_temp) * grad
        new_grad = self.activation_diff_grad @ self.weight.T
        # 重点🚨！！！ self.x_temp.T @ activation_diff_grad 便是 loss 对 weight 的导数
        self.weight -= lr * self.x_temp.T @ self.activation_diff_grad
        self.bias -= lr * self.activation_diff_grad

        return new_grad

class NetWork:
    def __init__(self):
        self.layers = []
        # 这里使用前边 tensorflow 的权重、偏置
        # 注意了??！ 这里要把参数转为 numpy 类型
        self.linear_1 = Linear(w1.numpy(), b1.numpy(), activation=relu)
        self.linear_2 = Linear(w2.numpy(), b2.numpy(), activation=sigmoid)
        self.linear_3 = Linear(w3.numpy(), b3.numpy(), activation=sigmoid)

    def __call__(self, x):
        x = self.linear_1(x, self)
        x = self.linear_2(x, self)
        x = self.linear_3(x, self)

        return x

    def fit(self, x, y, epochs):
        for epoch in range(epochs):
            pred = self(x)
            self.backward(y, pred)

    def backward(self, true, pred):
        print('mse-loss:', mse(true, pred))
        grad = mse.diff(true, pred)
        for layer in reversed(self.layers):
            grad = layer.update(grad)
        # 重点🚨！！！ 这里只输出最后一次的计算结果
        print('loss 对 w1 的导数:\n', self.linear_1.x_temp.T @ self.linear_1.activation_diff_grad)

network = NetWork()

# 迎接你们的亡！！！👺
# 注意了??！ 这里要把参数转为 numpy 类型（因为这里的数据都是上面 tensorflow 的，转成 numpy 格式才行）
network.fit(x.numpy(), true.numpy(), 1)
==============================
输出：
mse-loss: [[0.43199557]]
loss 对 w1 的导数:
[[0.00111374 0.0012263 0.00095062 0.00114191] [0.00020771 0.0002287 0.00017729 0.00021296]]

快快快！你看 ?????? 两者的结果是一样的，说明手搓出来的是对的

。k 文章水完啦 🥳🎉🎊
哇趣…写的真是累喂~ (#`O′)

没用的冷知识：整篇文章由ipynb改的，若要运行验证，每段直接copy至ipynb文件

文章来源:https://blog.csdn.net/kkkaiyu/article/details/135184157
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！