Python实现稳健线性回归模型(rlm算法)项目实战

说明：这是一个机器学习实战项目（附带数据+代码+文档+视频讲解），如需数据+代码+文档+视频讲解可以直接到文章最后获取。

1.项目背景

稳健回归可以用在任何使用最小二乘回归的情况下。在拟合最小二乘回归时，我们可能会发现一些异常值或高杠杆数据点。已经确定这些数据点不是数据输入错误，也不是来自另一个群落。所以我们没有令人信服的理由将它们排除在分析之外。

稳健回归可能是一种好的策略，它是在将这些点完全从分析中排除；和包括所有数据点；以及在OLS回归中平等对待所有数据点之间的妥协。他可以个给每个样本一个权重，离群值权重低一些，正常值权重高一些，进行校正。

本项目通过RLM回归算法来构建稳健线性回归模型。 ?

2.数据获取

本次建模数据来源于网络(本项目撰写人整理而成)，数据项统计如下：

编号	变量名称	描述
1	rownames
2	type
3	income
4	education
5	prestige

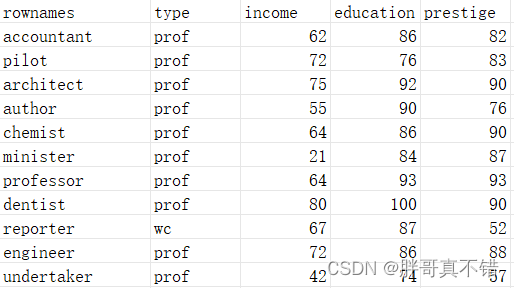
数据详情如下(部分展示)：

3.数据预处理

3.1?用Pandas工具查看数据

使用Pandas工具的head()方法查看前五行数据：

关键代码：

3.2 数据缺失查看

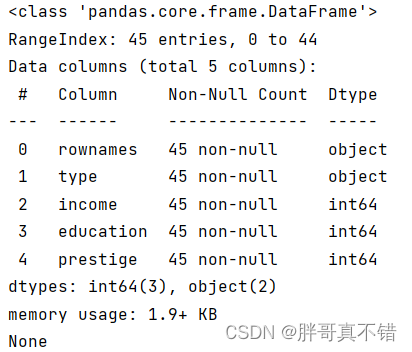
使用Pandas工具的info()方法查看数据信息：

??????

从上图可以看到，总共有5个变量，数据中无缺失值，共45条数据。

关键代码：

3.3?数据描述性统计

通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。

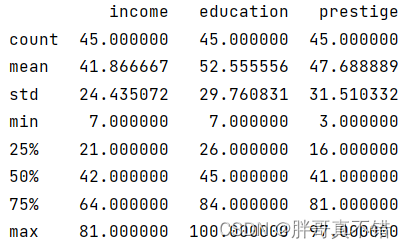
关键代码如下： ???

4.探索性数据分析

4.1?变量直方图

用Matplotlib工具的hist()方法绘制直方图：

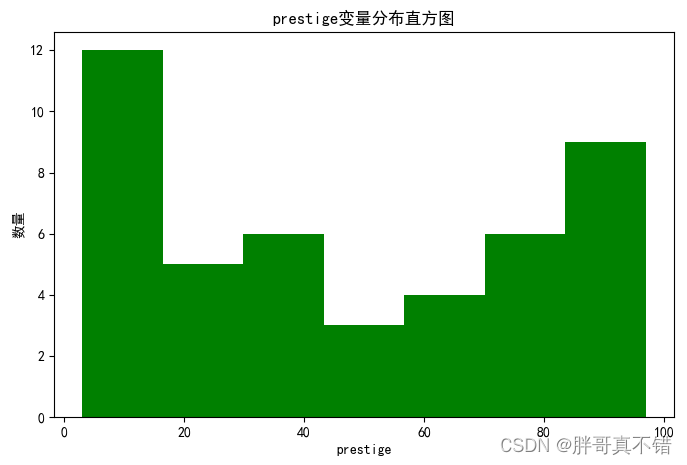
从上图可以看到，变量主要集中在20~80之间。 ?

4.2 相关性分析

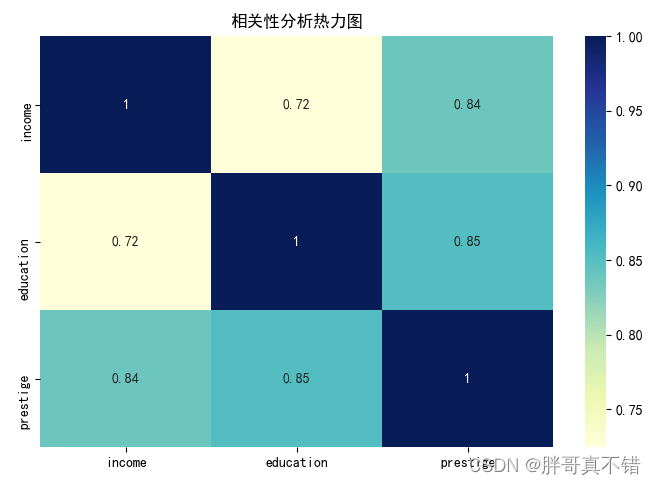
从上图中可以看到，数值越大相关性越强，正值是正相关、负值是负相关。

5.构建稳健线性回归模型

主要使用RLM回归算法，用于目标回归。

5.1 构建模型

编号	模型名称	参数
1	稳健线性回归模型	默认参数

5.2 模型摘要信息

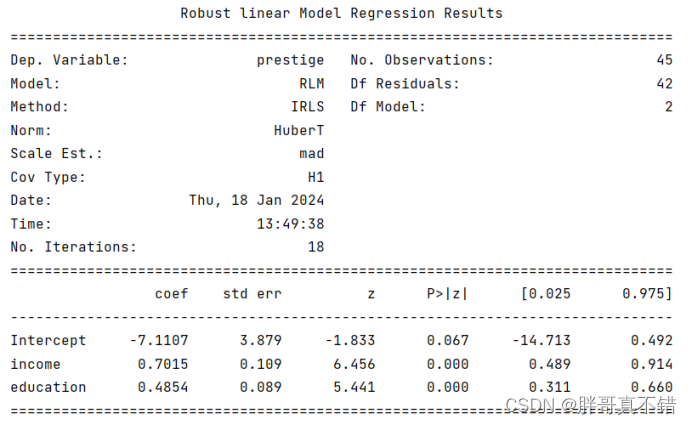
6.模型评估

6.1?评估指标及结果

评估指标主要包括可解释方差值、平均绝对误差、均方误差、R方值等等。

模型名称	指标名称	指标值
测试集
稳健线性回归模型	??R方	0.8251
	均方误差	169.7509
	可解释方差值	0.8252
	平均绝对误差	9.4373?

从上表可以看出，R方为0.8251，说明模型效果良好。

关键代码如下：

6.2?真实值与预测值对比图

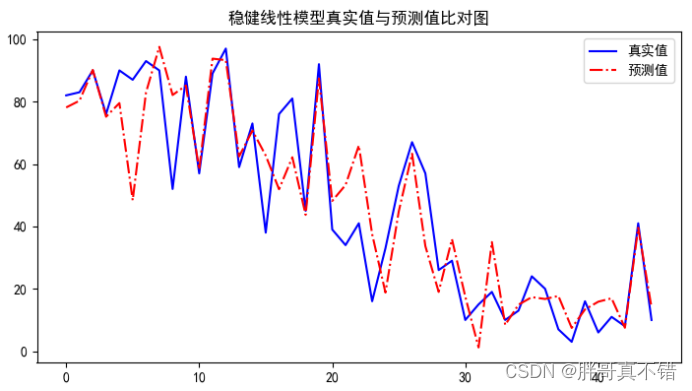
从上图可以看出真实值和预测值波动基本一致。 ?

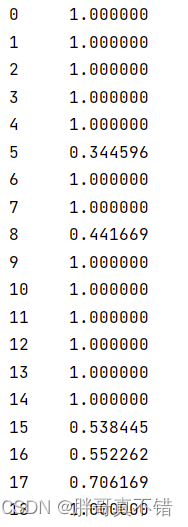
6.3?观测值的权重

观测值比较多，这里进行部分展示：

7.结论与展望

综上所述，本文采用了RLM回归算法来构建回归模型，最终证明了我们提出的模型效果良好。此模型可用于日常产品的预测。

# 本次机器学习项目实战所需的资料，项目资源如下：
 
# 项目说明：
 
# 获取方式一：
 
# 项目实战合集导航：
 
https://docs.qq.com/sheet/DTVd0Y2NNQUlWcmd6?tab=BB08J2
 
# 获取方式二：

链接：https://pan.baidu.com/s/1fcwNm3yh8ZuVpV1Nv7WfMQ 
提取码：ij6e