二叉树（性质+遍历+线索化）

发布时间：2024年01月14日

目录

一、性质

二、二叉树的创建，和插入

三、二叉树的遍历

1.层序（次）遍历--广度优先遍历

2.深度优先遍历：先序遍历，中序遍历，后序遍历 （递归）

3.两种遍历的完整代码

4.深度优先队列（非递归）

4.1先序遍历

4.2 中序遍历

4.3.后序遍历

4.4完整代码

5.关于二叉树遍历的问题

四、线索化二叉树

1.背景

2.概念

3.如何线索化（先序线索化，中序线索化，后序线索化）

3.1 中序线索化

3.2 前序线索化 ，后序线索化

3.3 完整代码

4.中序线索化找前驱和后继

（1）如何找x节点后继：

（2）如何找x节点前驱

（3）代码

5.应用场景

一、性质

1.第n层最多有（2^{n-1}）个节点

2.深度为n的树最多有（2^{n}-1）个节点

3.叶子节点=度为2的节点+1

4.一棵完全二叉树有n个节点，它的深度为?\left \lfloor \log n+1 \right \rfloor?/?\left \lceil \log\left ( n+1\right ) \right \rceil

二、二叉树的创建，和插入

#include <bits/stdc++.h>
typedef struct BTNode{
    char data;
    struct BTNode* left;
    struct BTNode* right;
}BTNode,*BTree;//二叉树的创建
int flag;//=0 左 ；=1 右
BTree initTree(char x)
{
    BTNode* r=(BTNode*)malloc(sizeof(BTNode));
    if(r==NULL)
    {
        printf("错误\n");
        return NULL;
    }
    else{
        r->data=x;
        r->left = r->right=NULL;
        return r;
    }
    
}
BTNode* find(BTree ro,char fx)//找父亲节点
{//递归
    if(ro==NULL||ro->data==fx)
    {
        return ro;
     }
     if(ro->left!=NULL)
     {
         BTNode* f=find(ro->left ,fx);
         if(f!=NULL&&f->data==fx)
         {
             return f;
         }
     }
     if(ro->right !=NULL)
     {
         BTNode* f=find(ro->right ,fx);
         if(f!=NULL&&f->data==fx)
         {
             return f;
         }
     }
     return NULL;
    
}
void insert(BTree ro,char x,char fx,int flag)
{
    BTNode* f=find(ro,fx);
    if(f!=NULL)
    {
        BTNode* s=(BTNode*)malloc(sizeof(BTNode));
        s->data=x;
        s->left=s->right=NULL;
        if(flag==0)
        {
            f->left=s;
        }
        else{
            f->right=s;
        }
    }
}
int main()
{
    int n;
    char x,fx;
    BTree ro=NULL;
    scanf("%d",&n);
    getchar();
    scanf("%c",&x);
    ro=initTree(x);
    for(int i=2;i<=n;i++)
    {
        getchar();
        scanf("%c %c %d",&x,&fx,&flag);
        insert(ro,x,fx,flag);
    }
    getchar();
    scanf("%c",&x);
    BTNode* p=find(ro,x);
    if(p!=NULL)
    {
        if(p->left!=NULL)
        {
            printf("左%c\n",p->left->data );
        }
        if(p->right !=NULL)
        {
            printf("右%c\n",p->right ->data );
        }
    }
    return 0;
     
}

三、二叉树的遍历

1.层序（次）遍历--广度优先遍历

遍历顺序：从上往下，依次输出每一层（左->又）的节点

如何实现？

当我们访问一个节点时，直接把这个节点的孩子存下来，后面遍历到某个节点时，直接去存放的地方找即可。（使用链式队列实现）

（1）声明队列

（2）根节点入队

（3）循环：只要队列非空，队首元素出队，访问队首元素，并且将队首的左右孩子（非空）依 ? 次入队。

2.深度优先遍历：先序遍历，中序遍历，后序遍历 （递归）

先序遍历：中 左 右 （“中”在最“先”）

中序遍历：左 中 右 （“中”在“中”间）

后序遍历：左 右 中 （“中”在“后”面）

3.两种遍历的完整代码

#include<bits/stdc++.h>
typedef struct BTNode{
    char data;
    struct BTNode* left;
    struct BTNode* right;
}BTNode,*BTree;
int flag;


typedef struct qnode{
    char data;
    struct qnode* next;
}qnode,*lqueue;
lqueue front,rear;
void initqueue()
{
    qnode* q=(qnode*)malloc(sizeof(qnode));
    if(q==NULL)
    {
        printf("错误\n");
        return;
    }
    front=rear=q;
    front->next=NULL;
}
void enqueue(char x)
{
    qnode* s=(qnode*)malloc(sizeof(qnode));
    s->data=x;
    s->next=NULL;
    rear->next=s;
    rear=s;
}
int empty()
{
    if(front->next==NULL)
    {
        return 1;//空
    }
    return 0;//非空
}
char dequeue()
{
    if(!empty())
    {
        qnode* q=front->next;
        front->next=q->next;
        char x=q->data;
        if(front->next==NULL)
        {
            rear=front;
        }
        free(q);
        q=NULL;
        return x;
        
     }
     else{
         printf("队空\n");
         return ' ';
     }
    
}
//----------------------------
//?二叉树
BTree initTree(char x)
{
    BTNode* r=(BTNode*)malloc(sizeof(BTNode));
    if(r==NULL)
    {
        printf("错误\n");
        return NULL;
    }
    else{
        r->data=x;
        r->left = r->right=NULL;
        return r;
    }
    
}
BTNode* find(BTree ro,char fx)
{
    if(ro==NULL||ro->data==fx)
    {
        return ro;
     }
     if(ro->left!=NULL)
     {
         BTNode* f=find(ro->left ,fx);
         if(f!=NULL&&f->data==fx)
         {
             return f;
         }
     }
     if(ro->right !=NULL)
     {
         BTNode* f=find(ro->right ,fx);
         if(f!=NULL&&f->data==fx)
         {
             return f;
         }
     }
     return NULL;
    
}
void insert(BTree ro,char x,char fx,int flag)
{
    BTNode* f=find(ro,fx);
    if(f!=NULL)
    {
        BTNode* s=(BTNode*)malloc(sizeof(BTNode));
        s->data=x;
        s->left=s->right=NULL;
        if(flag==0)
        {
            f->left=s;
        }
        else{
            f->right=s;
        }
    }
}
void levelOrderBTree(BTree ro) //广度优先遍历
{
    char x;
    BTNode* q=NULL;
    initqueue();//初始化队列
    if(ro==NULL)
    {
        printf("空树\n");
        return ;
     }
     enqueue(ro->data);//根节点数据入队
    while(!empty())
    {
        x=dequeue();
        printf("%c ",x);
        q=find(ro,x);
        if(q->left!=NULL)
        {
            enqueue(q->left->data);
        }
        if(q->right!=NULL)
        {
            enqueue(q->right->data);
        }
    
     }
     
}
void perOrder(BTree ro) //先序遍历
{
    if(ro==NULL)
    {
        return;
    }
    printf("%c ",ro->data);
    if(ro->left!=NULL)
    {
        perOrder(ro->left);
    }
    if(ro->right !=NULL)
    {
        perOrder(ro->right);
    }
}
void inOrder(BTree ro) //中序遍历
{
    if(ro==NULL)
    {
        return;
    }
    
    if(ro->left!=NULL)
    {
        inOrder(ro->left);
    }
    printf("%c ",ro->data);
    
    if(ro->right !=NULL)
    {
        inOrder(ro->right);
    }
}
void postOrder(BTree ro) //后序遍历
{
    if(ro==NULL)
    {
        return;
    }
    
    if(ro->left!=NULL)
    {
        postOrder(ro->left);
    }
    
    if(ro->right !=NULL)
    {
        postOrder(ro->right);
    }
    printf("%c ",ro->data);
}
int main()
{
    int n;
    char x,fx;
    BTree ro=NULL;
    scanf("%d",&n);
    getchar();
    scanf("%c",&x);
    ro=initTree(x);
    for(int i=2;i<=n;i++)
    {
        getchar();
        scanf("%c %c %d",&x,&fx,&flag);
        insert(ro,x,fx,flag);
    }
    levelOrderBTree(ro);
    printf("\n");
    perOrder(ro);
    printf("\n");
    inOrder(ro);
    printf("\n");
    postOrder(ro);
    return 0;
     
}

4.深度优先队列（非递归）

4.1先序遍历

? ?根 左子树 右子树

（1）从根节点开始遍历，根节点入栈

（2）循环：栈非空，取出栈顶元素，访问栈顶元素（输出），将栈顶元素的右左元素的右左孩子节点依次入栈

（3)栈空结束

下面为例子：

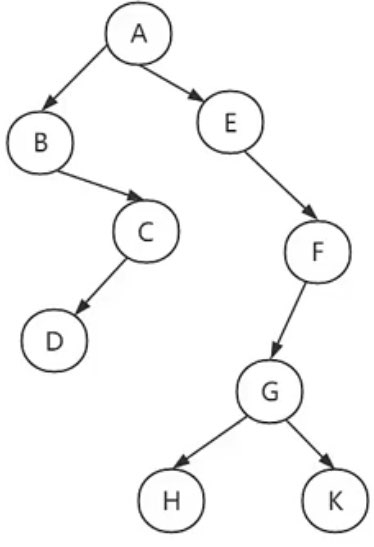
第一步：A入栈（A）

第二步：输出A，A出栈，E，B入栈?（E，B）

第三步：输出B，B出栈，C入栈（E，C）

第四步：输出C，C出栈，D入栈（E，D）

第五步：输出D，D出栈（E）

第六步：输出E，E出栈，F入栈（F）

第七步：输出F，F出栈，G入栈（G）

第八步：输出G，G出栈，K，H入栈（K，H）

第九步：输出H（K）

第十步：输出K

综上，输出顺序为：A B C D E F G H K

4.2 中序遍历

左子树 根 右子树

（1）从根节点开始遍历，令node=ro; node入栈（ro是根节点）

（2）循环：栈非空或node非空，如果node非空，node入栈，node=node->左孩子，如果node==NULL,此时可以访问栈顶元素，node=栈顶元素的右孩子,栈顶出栈，访问（输出）栈顶元素

（3）循环结束

第一步：A入栈（A）node=B

第二步：B入栈（A，B）node=NULL

第三步： 访问B，B出栈（A）node=C

第四步：C入栈（A，C）node=D

第五步：D入栈（A，C，D）node=NULL

第六步：访问D，D出栈（A，C) node=NULL

第七步：访问C，C出栈（A）node=NULL

第八步：访问A，A出栈（）node=E

第九步：E入栈（E）node=NULL

第十步：访问E，E出栈（）node=F

十一步：F入栈（F）node=G

十二步：G入栈（F，G）node=H

十三步：H入栈（F，G，H）node=NULL

十四步：访问H，H出栈（F，G）node=NULL

十五步：访问G，G出栈（F）node=K

十六步：K入栈（F，K）node=NULL

十七步：访问K，K出栈（F）node=NULL

十八步：访问F，F出栈（）node=NULL

综上，访问顺序为：B D C A E H G K F

4.3.后序遍历

左子树 右子树 根

（1）从根节点开始遍历，令node=ro，pre=NULL? (ro是根节点，pre是上一个访问的）

（2）循环：栈非空或node非空，如果node非空，node入栈，node=node->左孩子，如果node==NULL：判断栈顶元素的右孩子是否存在并没有访问过，如存在并且没有被访问过继续遍历栈顶的右孩子；否则访问栈顶，pre=栈顶，node=NULL

（3）循环结束

第一步：A入栈（A）node=B,pre=NULL

?第二步：B入栈（A，B）node=NULL,pre=NULL

第三步：C入栈（A，B，C）node=D,pre=NULL

第四步：D入栈（A，B，C，D）node=NULL,pre=NULL

第五步：访问D，D出栈 （A，B，C）node=NULL,pre=D

第六步：访问C，C出栈（A，B）node=NULL,pre=C

第七步：访问B，B出栈（A）node=NULL,pre=B

第八步：E入栈（A，E）node=NULL,pre=B

第九步：F入栈（A，E，F）node=G,pre=B

第十步：G入栈（A，E，F，G）node=H,pre=B

十一步：H入栈（A，E，F，G，H）node=NULL,pre=B

十二步：访问H，H出栈（A，E，F，G）node=NULL,pre=H

十三步：K入栈（A，E，F，G，K）node=NULL,pre=H

十四步，访问K，K出栈（A，E，F，G）node=NULL,pre=K

十五步：访问G，G出栈（A，E，F）node=NULL,pre=G

十六步：访问F，F出栈（A，E）node=NULL,pre=F

十七步：访问E，E出栈（A）node=NULL,pre=E

十八步：访问A，A出栈（）node=NULL,pre=A

综上，访问顺序为：D C B H K G F E A

4.4完整代码
#include <stdlib.h>
#include <stdio.h>
# include <string.h>
// 树的节点结构
typedef struct BTNode{
    char data;
    struct BTNode* left;
    struct BTNode* right;
}BTNode,*BTree;
int flag;//=0 左孩子， =1 右孩子
//---------------------链栈----------------------
//单链表的节点结构：将整个节点入队
typedef struct stackNode{
    struct BTNode* data;
    struct stackNode* next;
}sstack;
sstack* s=NULL;
//初始化链栈
void initstack()
{
    s=(sstack*)malloc(sizeof(sstack));
    if(s==NULL)
    {
        printf("栈空间分配失败\n");
        return ;
    }
    s->next=NULL;
}
//入栈
void ppush(BTNode* k)
{//头插法
    sstack* p=(sstack*)malloc(sizeof(sstack));
    p->data=k;
    p->next=s->next;
    s->next=p;
    
}
//判空
int empty()
{
    if(s->next==NULL)
    {
        return 1;
    }
    return 0;
 }
//出栈：返回栈顶元素，将其在栈中删除
BTNode* ppop()
{
    if(empty()==1)
    {
        printf("栈空\n");
        return NULL;
    }
    sstack* p=s->next;
    BTNode* k=s->next->data;
    s->next=p->next;
    free(p);
    p=NULL;
    return k;
}
//---------------------------------------------------------------

BTree initTree(char x)
{
    BTNode* r=(BTNode*)malloc(sizeof(BTNode));
    if(r==NULL)
    {
        printf("错误\n");
        return NULL;
    }
    else{
        r->data=x;
        r->left = r->right=NULL;
        return r;
    }
    
}
BTNode* find(BTree ro,char fx)
{
    if(ro==NULL||ro->data==fx)
    {
        return ro;
     }
     if(ro->left!=NULL)
     {
         BTNode* f=find(ro->left ,fx);
         if(f!=NULL&&f->data==fx)
         {
             return f;
         }
     }
     if(ro->right !=NULL)
     {
         BTNode* f=find(ro->right ,fx);
         if(f!=NULL&&f->data==fx)
         {
             return f;
         }
     }
     return NULL;
    
}
void insert(BTree ro,char x,char fx,int flag)
{
    BTNode* f=find(ro,fx);
    if(f!=NULL)
    {
        BTNode* s=(BTNode*)malloc(sizeof(BTNode));
        s->data=x;
        s->left=s->right=NULL;
        if(flag==0)
        {
            f->left=s;
        }
        else{
            f->right=s;
        }
    }
}
//--------------------------
//先序遍历
void perOrder(BTree ro)
{
    initstack();//初始化栈
    if(ro==NULL)
    {
        return;
     }
     ppush(ro);
     while(!empty())
     {
         BTNode* node=ppop();
         printf("%c ",node->data);
        if(node->right!=NULL)
        {
            ppush(node->right);
         }
         if(node->left !=NULL)
        {
            ppush(node->left );
         }
         
     }
    
}
void inOrder(BTree ro)
{
    initstack();//≥? oa?“a∏?’a
    if(ro==NULL)
    {
        return;
     }
     BTNode* node=ro;
     BTNode* k=NULL;
     while(!empty()||node!=NULL)
     {
         if(node!=NULL)
         {
             ppush(node);
             node=node->left;
         }
         else{
             k=ppop();//?°≥?’a??K
             printf("%c ",k->data);
             node=k->right;
         }
     }
    
 }
void postOrder(BTree ro)
{
    initstack();//≥? oa?“a∏?’a
    if(ro==NULL)
    {
        return;
     }
    BTNode* node=ro;
    BTNode* k=NULL;
    BTNode* pre=NULL;
     while(!empty()||node!=NULL)
     {
         if(node!=NULL)
         {
             ppush(node);
             node=node->left;
        }
        else
        {
            k=s->next->data;//’a??‘?à?
            if(k->right!=NULL&&pre!=k->right)
            {
                node=k->right;
             }
             else
             {
                 k=ppop();
                 printf("%c ",k->data);
                 pre=k;
                 node=NULL;//∑μa?…?“a∏?∏∏??Ω·μ?
             }
        }
         
     }
     
}
int main()
{
    int n;
    char x,fx;
    BTree ro=NULL;
    scanf("%d",&n);
    getchar();
    scanf("%c",&x);
    ro=initTree(x);
    for(int i=2;i<=n;i++)
    {
        getchar();
        scanf("%c %c %d",&x,&fx,&flag);
        insert(ro,x,fx,flag);
    }
    

    //perOrder(ro);     //??–ú±è?˙--∑?μ?πè
    //inOrder(ro);//÷––ú±è?˙--∑?μ?πè
    postOrder(ro);//∫?–ú±è?˙--∑?μ?πè
    printf("\n");
    
    
    return 0;
     
}

5.关于二叉树遍历的问题

已知

（1）中序+先序-->先序第一个一定是根节点

（2）中序+后序-->?后序最后一个一定是根节点

（3）中序+层序-->层序第一个一定是根节点

求剩下两种序列？

eg.

先序：1 2 3 4 5 6

中序：3 2 4 1 6 5

（1）首先，从先序来看，我们知道1是先序的第一个元素，也是这棵二叉树的根节点。

（2）接着，我们找中序里面对应的1的位置，找到了之后，我们发现3 2 4是在1的左边，也就是说这些都是1的左孩子，先不管这些内部复杂的亲子兄弟关系了。6 5是在1的右边，也就是说这些都是1的右孩子。

（3）在先序中找2 3 4的第一个，是2，在中序里面对应的2左边是3，右边是4，分别是它的左右孩子。

（4）在先序中找6 5，发现第一个是5，在中序里面对应的5地左边是6，右边没有，也就是说，5只有一个左孩子，是6。

（5）由此得到的树为：

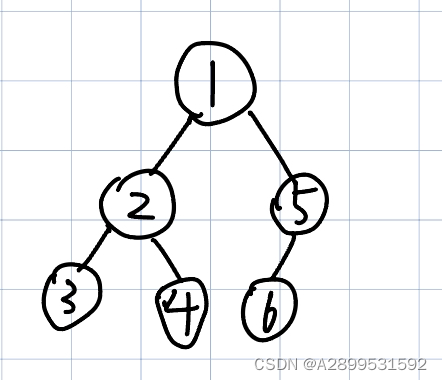
已知中序和后序的也很类似，就不详述了。

四、线索化二叉树

1.背景

n个节点的二叉树，二叉链表存储，一共会有2n个指针域，n-1个真正存了指针的，n+1个是空的

-------->极大的空间浪费。

设二叉树的一个节点H，求H的中序遍历序列的前驱和后继分别是谁？

法一：（1）先进行中序遍历，得到序列

? ? ? ? ? ?（2）遍历序列，先找到H在序列中的位置，然后前后位置就是答案

法二：线索化

2.概念

线索化：

（1）如果一个节点其左孩子指针域为空，那么就将该指针域指向其前驱节点

（2）如果一个节点其右孩子指针域为空，那么就将该指针域指向其后驱节点

这种指向前驱和后继的指针称为 线索 。将?棵普通?叉树以某种次序遍历，并添加线索的过程称为线索化。

3.如何线索化（先序线索化，中序线索化，后序线索化）

我们如何区分?个结点的 lchild指针是指向左孩?还是前驱结点呢？

为了解决这?问题，现需要添加标志位 lflag ， rflag 。并定义规则如下：
lflag 为 0 时，指向左孩?，为 1 时指向前驱 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
rflag 为 0 时，指向右孩?，为 1 时指向后继
3.1 中序线索化

在先前代码基础上把??访问 改为 加线索

访问一个节点x时，pre是其前驱，对应的?x是pre的后继

如果x->left==NULL，x->left=pre

如果pre->right==NULL，pre->right=x

3.2 前序线索化 ，后序线索化

线索化以后，因为每个节点都有左右孩子了，注意把前序，后序判断条件修改一下。其他和中序线索化一样。（中序不会有这个问题，因为中序在线索化前已经判断完了）? ? ?

3.3 完整代码

代码主要加了一个visit（）函数

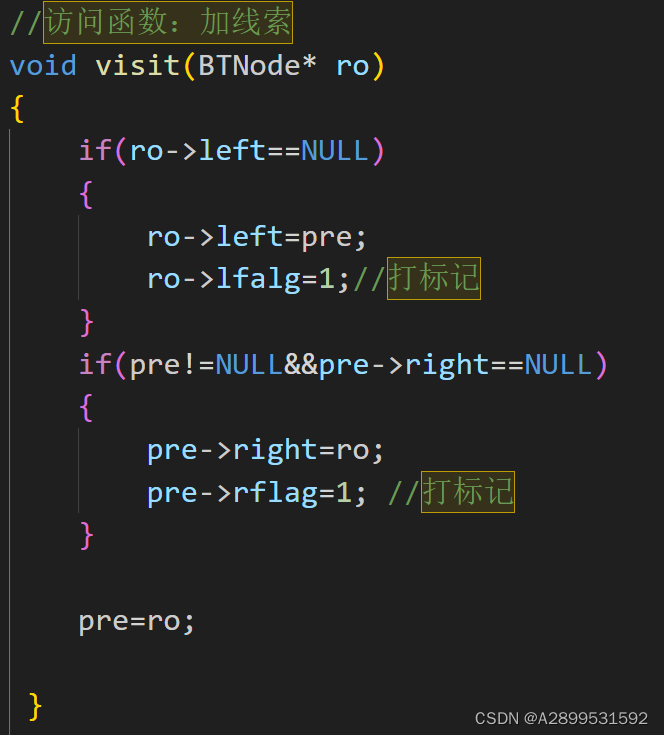
完整代码如下

#include <stdlib.h>
#include <stdio.h>
# include <string.h>
typedef struct BTNode{
	char data;
	struct BTNode* left;
	struct BTNode* right;
	int lfalg,rflag;//标记左右指针指向的是孩子节点（0），还是前驱后继（1）
}BTNode,*BTree; 
int flag;//=0 左孩子 =1 右孩子
BTNode* pre=NULL;
//---------------------------- 
//树的相关代码
BTree initTree(char x)
{
	BTNode* r=(BTNode*)malloc(sizeof(BTNode));
	if(r==NULL)
	{
		printf("分配失败\n"); 
		return NULL;
	}
	else{
		r->data=x;
		r->left = r->right=NULL;
		r->lfalg=r->rflag=0;
		return r; 
	}
	
}
BTNode* find(BTree ro,char fx)
{
	if(ro==NULL||ro->data==fx)
	{
		return ro;
	 } 
	 if(ro->left!=NULL&&ro->lfalg==0)
	 {
	 	BTNode* f=find(ro->left ,fx); 
	 	if(f!=NULL&&f->data==fx)
	 	{
	 		return f;
		 }
	 }
	 if(ro->right !=NULL&&ro->rflag==0)
	 {
	 	BTNode* f=find(ro->right ,fx); 
	 	if(f!=NULL&&f->data==fx)
	 	{
	 		return f;
		 }
	 }
	 return NULL;
	
}
void insert(BTree ro,char x,char fx,int flag)
{
	BTNode* f=find(ro,fx); 
	if(f!=NULL)
	{
		BTNode* s=(BTNode*)malloc(sizeof(BTNode));
		s->data=x;
		s->left=s->right=NULL;
		s->lfalg=s->rflag=0;
		if(flag==0)
		{
			f->left=s;
		}
		else{
			f->right=s;
		}
	}
}
//访问函数：加线索
void visit(BTNode* ro)
{
	if(ro->left==NULL)
	{
		ro->left=pre;
		ro->lfalg=1;//打标记
	}
	if(pre!=NULL&&pre->right==NULL)
	{
		pre->right=ro;
		pre->rflag=1; //打标记
	}
	
	pre=ro;
	
 } 

void perOrder(BTree ro) 
{
	if(ro==NULL)
	{
		return;
	}
	//printf("%c ",ro->data);
	visit(ro);
	if(ro->left!=NULL&&ro->lfalg==0)
	{
		perOrder(ro->left);
	}
	if(ro->right !=NULL&&ro->rflag==0)
	{
		perOrder(ro->right);
	}
}
//中序遍历函数--->加线索
void inOrder(BTree ro) 
{
	if(ro==NULL)
	{
		return;
	}
	
	if(ro->left!=NULL&&ro->lfalg==0) 
	{
		inOrder(ro->left);
	}
	
	//printf("%c ",ro->data);//访问
	visit(ro); //线索化
	
	if(ro->right !=NULL&&ro->rflag==0)
	{
		inOrder(ro->right);
	}
}
void postOrder(BTree ro) 
{
	if(ro==NULL)
	{
		return;
	}
	
	if(ro->left!=NULL&&ro->lfalg==0)
	{
		postOrder(ro->left);
	}
	
	if(ro->right !=NULL&&ro->rflag==0)
	{
		postOrder(ro->right);
	}
	//printf("%c ",ro->data);
	visit(ro);
}


int main()
{
	int n;
	char x,fx;
	BTree ro=NULL;
	scanf("%d",&n);
	getchar();
	scanf("%c",&x);
	ro=initTree(x);
	for(int i=2;i<=n;i++)
	{   
		getchar();
		scanf("%c %c %d",&x,&fx,&flag);
		insert(ro,x,fx,flag);
	}

    inOrder(ro);//
    getchar();
	scanf("%c",&x);
	BTNode* ans=find_pre(ro,x);
	if(ans==NULL)
	{
		printf("错误\n");
	 } 
	 else{
	 	printf("%c ",ans->data);
	 }

	return 0;	 
}

4.中序线索化找前驱和后继

中序线索化找前驱和后继比较方便，先序和后序不方便所以不考虑。

（1）如何找x节点后继：

? ? ? ? 1.1）x->rflag==1, x->right就是后继

? ? ? ? 1.2）x->rflag==0, x->right是右孩子，x的后继为x的右子树中最靠左的节点

p=x->right;
while(p->left!=NULL&&p->lflag==1)
{
    p=p->left;
}

????????p是x的后继节点

（2）如何找x节点前驱

? ? ? ? 2.1）x->lfalg==1,x->left就是前驱

? ? ? ? 2.2）x->lflag==0,x->left是左孩子，x的前驱节点为x的左子树中最靠右的节点

p=x->left;
while(p->right!=NULL&&p->rflag==1)
{
    p=p->right;
}

p是x的前驱节点

（3）代码
BTNode* find_pre(BTree ro,char k)
{
	BTNode* x=find(ro,k);
	if(x!=NULL)
	{
		if(x->lfalg==1)
		{
			return x->left;
		}
		else
		{
			if(x->left==NULL)
			{
				return NULL;
			}
			BTNode* p=x->left;
			while(p->right!=NULL&&p->rflag==0)
			{
				p=p->right;
			}
			return p;
		} 
	}
	
}
BTNode* find_post(BTree ro,char k)
{
	BTNode* x=find(ro,k);
	if(x!=NULL)
	{
		if(x->rflag ==1)
		{
			return x->right;
		}
		else
		{
			if(x->right==NULL)
			{
				return NULL;
			}
			BTNode* p=x->right;
			while(p->left !=NULL&&p->lfalg ==0)
			{
				p=p->left ;
			}
			return p;
		} 
	}
	
}

5.应用场景

优点：加快了找前驱和后继的速度

计算机网络：CIDR 选择下一跳 最长前缀匹配：线索化

文章来源:https://blog.csdn.net/A2899531592/article/details/135536594
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章