乳腺癌预测_EDA_Models

前言

在医学领域的不断创新中，技术的进步为疾病的早期预测和诊断提供了全新的可能性。乳腺癌作为女性最常见的癌症之一，对于其早期预测变得尤为关键。本文将引领您探索乳腺癌预测中的数据探索分析（Exploratory Data Analysis，简称EDA）以及相关的模型应用。通过深入挖掘乳腺癌数据集，我们将揭示隐藏在背后的模式和趋势，为医学领域的科学家、数据科学家和临床医生提供更有力的工具，以更准确地预测乳腺癌的风险。

数据介绍

1.概述

研究假设：本研究假设患者的诊断特征之间存在显着关联，包括年龄、绝经状态、肿瘤大小、侵入性淋巴结的存在、受影响的乳房、转移状态、乳房象限、乳房状况病史及其乳房癌症诊断结果。数据收集和描述：213 名患者观察数据的数据集是从卡拉巴尔大学教学医院癌症登记处获得的，历时 24 个月（2019 年 1 月至 2021 年 8 月）。数据包括十一个特征：诊断年份、年龄、绝经状态、肿瘤大小（厘米）、侵入性淋巴结数量、受影响的乳房（左或右）、转移（是或否）、受影响乳房的象限、乳房疾病史，以及诊断结果（良性或恶性）。值得注意的发现：经初步检查，数据显示不同患者特征的诊断结果存在差异。一个值得注意的趋势是，肿瘤尺寸较大且存在侵袭性淋巴结的患者中恶性结果的发生率较高。此外，绝经后妇女的恶性诊断率似乎更高。 解释和使用：可以使用统计和机器学习技术对数据进行分析，以确定患者特征与乳腺癌诊断之间关联的强度和显着性。这有助于建立乳腺癌早期检测和诊断的预测模型。但是，解释必须考虑潜在的限制，例如数据丢失或数据收集中的偏差。此外，这些数据反映的是来自一家医院的患者，限制了研究结果对更广泛人群的推广。这些数据对于有兴趣了解乳腺癌诊断因素和改善乳腺癌医疗保健策略的医疗保健专业人员、研究人员或政策制定者来说可能很有价值。它还可以用于有关乳腺癌相关危险因素的患者教育。

2.关于数据集

• S/N = 每个患者的唯一标识。
• Year=进行诊断的年份
• Age = 诊断时患者的年龄
• Menopause = 诊断时患者是否处于绝经期或绝经后，0 表示患者已达到更年期，而 1 表示患者尚未达到更年期。
• Tumor size = 切除肿瘤的大小（以厘米为单位）。
• Involved nodes = 含有转移性腋窝淋巴结的数量，“编码为存在或不存在的二元分布。1 表示存在，0 表示不存在。”
• Breast = 如果出现在左侧或右侧，“编码为二元分布 1 表示癌症已扩散，0 表示癌症尚未扩散。”
• Metastatic =如果癌症已扩散到身体或器官的其他部位。
• Breast quadrant = 腺体以乳头为中心点分为 4 个部分。
• History = 患者是否有癌症史或家族史，“1表示有癌症史，0表示无癌症史”。
• Diagnosis result = 乳腺癌数据集的实例。

预测过程

1.安装包

%%capture
!pip install catboost
!pip install pingouin
!pip install ppscore
!pip install pandas === 1.5.3
!pip install shap

• CatBoost: 用于梯度提升机器学习的库。
• Pingouin: 提供统计分析功能，包括各种统计测试和可视化。
• PPScore: 用于计算数据框之间的预测性性能得分。
• Pandas: 数据分析库，提供了强大的数据结构和数据分析工具。
• SHAP: 用于解释机器学习模型的库，特别适用于黑盒模型。

2.加载库

# Data Manipulation
#================================================
import pandas as pd
pd.set_option("display.max_columns", None)
import numpy as np

# Data visualization
#=================================================
import matplotlib.pyplot as plt
plt.style.use("ggplot")
import seaborn as sns
sns.set_style("darkgrid")

# Stats
#==============================================
import pingouin as pg
import statsmodels.api as sm
from scipy import stats
import ppscore as pps

# Data preprocessing
#==================================================
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import PowerTransformer
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.compose import ColumnTransformer

# Models
#==================================================
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from xgboost import XGBClassifier
from lightgbm import LGBMClassifier
from catboost import CatBoostClassifier


# Metrics
#========================================================
from sklearn.metrics import balanced_accuracy_score
from sklearn.metrics import confusion_matrix, classification_report
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import roc_curve, roc_auc_score

# shap
#===================================
import shap

# tqdm
#======================================================
from tqdm.auto import tqdm

# Counter
#====================================================
from collections import Counter

# warnings
#=============================================
import warnings
warnings.filterwarnings('ignore')

3.导入数据

data = pd.read_csv("/input/breast-cancer-prediction/breast-cancer-dataset.csv")

data.head()

获取数据集的行数和列数，并打印出这些信息

# 数据集大小
#==========================================================
rows, columns = data.shape[0], data.shape[1]

print(f'Rows: {rows}')
print(f'Columns: {columns}')

输出数据集的信息，包括每列的数据类型和非空值的数量

# Data set information
#================================================
print("==" * 30)
print(" " * 17, "Data set Information")
print("==" * 30)
print(data.info())

4.数据清洗

我们将删除每个变量名称中的空值，将数据集中列名中的空格替换为空字符串

data.columns = data.columns.str.replace(" ", "")
data.columns

检查数字列是否只包含数字值，不包含其他字符。为此，我们将选择数字列，然后将它们转换为数字类型，发现的错误将转换为 NaN。

对于列 Year, Age, Menopause, TumorSize(cm), Inv-Nodes, Metastasis, History，使用了 Pandas 的 to_numeric 方法进行转换。在这里，使用了 errors='coerce' 参数，将无法转换的值设为 NaN。

cols_to_verifier = ['Year', 'Age', 'Menopause', 'TumorSize(cm)', 
                    'Inv-Nodes', 'Metastasis', 'History']

for col in cols_to_verifier:
    data[col] = pd.to_numeric(data[col], errors = 'coerce')
    
data.head()

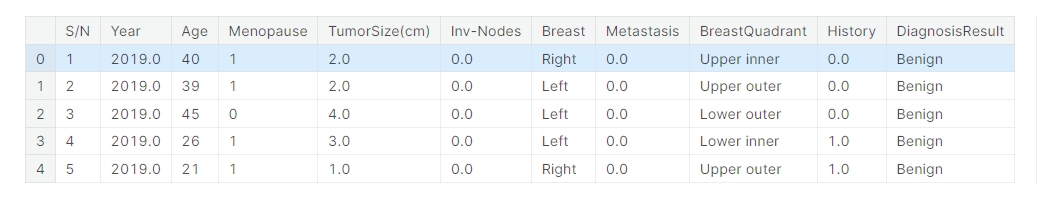
现在让我们检查其他每个变量是否只取正确的值，即数据集中描述的值。

• Menopause

data['Menopause'].unique()

可以看到只采用这两个数值

• Inv-Nodes

data['Inv-Nodes'].unique()

这个变量应该只取两个值，0和1，但是我们发现了4个值，所以让我们修改它。找到的其他字符将转换为 NaN。

data['Inv-Nodes'] = data['Inv-Nodes'].apply(lambda x: x if x == 0. or x == 1. else np.nan)

• Breast

data['Breast'].unique()

我们发现一个不正确的字符，让我们将其转换为 NaN。

data['Breast'] = data['Breast'].apply(lambda x: x if x == "Right" or x == "Left" else np.nan)

• Metastasis

data['Metastasis'].unique()

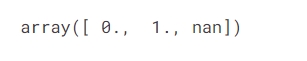
我们发现了一个 nan 值，因此为了确保它是 NaN 值，让我们将其转换为 NaN。

data['Metastasis'] = data['Metastasis'].apply(lambda x: x if x == 0. or x == 1. else np.nan)

• BreastQuadrant

data['BreastQuadrant'].unique()

我们发现了一个不需要的字符 (#) 和一些关于值“Upperouter”的空格。

data['BreastQuadrant'] = data['BreastQuadrant'].str.replace(' ', '')

data['BreastQuadrant'] = data['BreastQuadrant'].apply(lambda x: np.nan if x == '#' else x)

• DiagnosisResult

data['DiagnosisResult'].unique()

最后，目标变量的值不会出现任何错误。 至此我们成功修改了所有变量。

5.EDA

重复行

print(data.duplicated().sum())

不存在重复行。在继续分析之前，我们将删除第一列“Y/N”，因为它不会为我们的分析增加价值。

data = data.drop('S/N', axis = 1)

data.head()

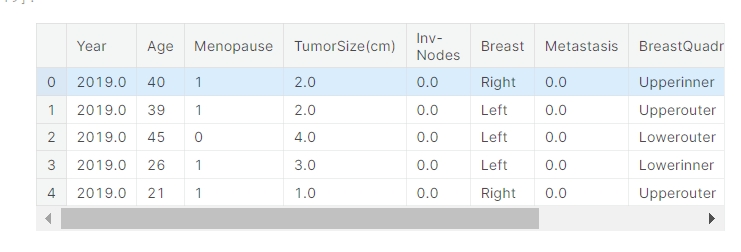
现在让我们检查是否存在缺失值。我们将首先找出缺失值的数量，然后找出它们的位置。

缺失值

df_null_values = data.isnull().sum().to_frame().rename(columns = {0:'count'})
df_null_values['%'] = (df_null_values['count'] / len(data)) * 100.
df_null_values = df_null_values.sort_values('%', ascending = False)
df_null_values

1. 使用 isnull() 方法检测数据集中的缺失值。
2. 使用 sum() 方法计算每列的缺失值数量。
3. 将结果转换为 DataFrame，并重命名列名为 ‘count’。
4. 计算每列缺失值的百分比，并添加到 DataFrame 中。
5. 根据缺失值百分比对 DataFrame 进行降序排序。

这个 DataFrame (df_null_values) 将显示每个列的缺失值数量和相应的百分比，以帮助你了解数据集中的缺失情况。

# We look for where the missing values are located.
#====================================================================
null_values = data[data.isnull().any(axis = 1)]
print(f'Cantidad total de filas con valores perdidos: {len(null_values)}')
null_values

缺失值的总行数：9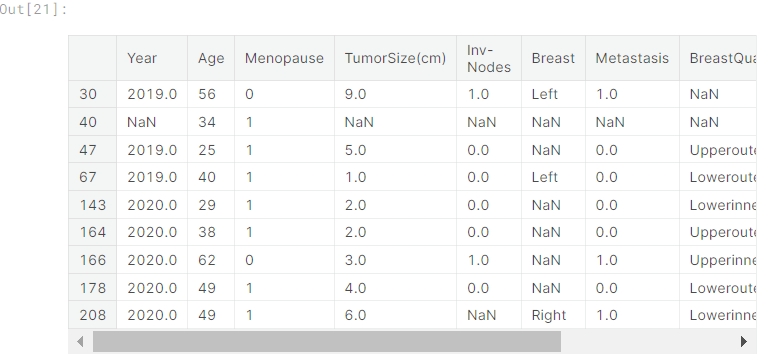

总共只有 9 行，因为我们不知道这些缺失值的来源，而且这个数量很小，所以我们将从数据集中将其删除。

data = data.dropna()

检查一下所有缺失值是否已被删除。

data.isnull().sum()

我们将生成数据的副本来执行 EDA，因为如果我们在原始数据集上执行它，可能会修改它并产生错误。

data_eda = data.copy()
data_eda.head()

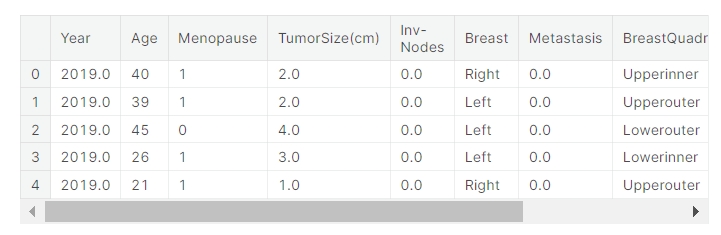
因为我们要进行分析，所以必须将二进制变量 (0/1) 转换为 (No/Yes) 以更好地理解绘图。

data_eda['Menopause'] = data_eda['Menopause'].apply(lambda x: "Yes" if x == 1 else "No")
data_eda['Metastasis'] = data_eda['Metastasis'].apply(lambda x: "Yes" if x == 1 else "No")
data_eda['Inv-Nodes'] = data_eda['Inv-Nodes'].apply(lambda x: "Yes" if x == 1 else "No")
data_eda['History'] = data_eda['History'].apply(lambda x: "Yes" if x == 1 else "No")

单变量分析

cols_to_plot = ['Age', 'TumorSize(cm)']
colors = sns.color_palette(palette = 'mako', n_colors = len(cols_to_plot))

fig,ax = plt.subplots(nrows = 1, ncols = 2, figsize = (9,4))
ax = ax.flat
for i,col in enumerate(cols_to_plot):
    sns.kdeplot(data_eda, x = col, alpha = 0.6, fill = True, linewidth = 2.5, color = colors[i], ax = ax[i])
    sns.histplot(data_eda, x = col, stat = 'density', fill = False, color = colors[i], ax = ax[i])
    sns.rugplot(data_eda, x = col, color = colors[i], ax = ax[i])
    ax[i].set_xlabel("")
    ax[i].set_title(col, fontsize = 11, fontweight = "bold", color = "black")
    
fig.suptitle("Distribution of variables", fontsize = 13, fontweight = "bold", color = "darkblue")
fig.tight_layout()
fig.show()

这里使用了 Seaborn 库来绘制核密度估计图和直方图，展示 ‘Age’ 和 ‘TumorSize(cm)’ 列的数据分布。每个图包括了核密度曲线、直方图和数据点的标尺。

cols_to_plot = ['Age', 'TumorSize(cm)']

fig,ax = plt.subplots(nrows = 1, ncols = 2, figsize = (9,4))
ax = ax.flat
for i,col in enumerate(cols_to_plot):
    pg.qqplot(data[col], ax = ax[i])
    ax[i].set_title(col, fontsize = 11, fontweight = "bold", color = "black")
    
fig.suptitle("QQ-Plots", fontsize = 13, fontweight = "bold", color = "darkblue")
fig.tight_layout()
fig.show()

这里使用了 Pingouin 库的 qqplot 函数来绘制 QQ 图，用于检查数据是否符合正态分布。如果数据点在QQ图中近似对角线上，则表示数据近似于正态分布。

正态性检验

def normality_test(name:str):
    p_value = stats.shapiro(data[name])[1]
    decision = "No Normal Distribution" if p_value < 0.05 else "Normal Distribution"
    return decision

print("--------------------------------------------")
print(" "*5, "Normal Test: Shapiro-Wilk")
print("--------------------------------------------")
for col in cols_to_plot:
    print(f'* {col}: {normality_test(col)}')

总之，没有一个变量来自正态分布的总体

cols_to_plot = ['Menopause', 'Inv-Nodes', 'Breast', 'Metastasis', 
                'History', 'BreastQuadrant', 'DiagnosisResult']

def autopct_fun(abs_values):
    gen = iter(abs_values)
    return lambda pct: f"{pct:.1f}%\n({next(gen)})"

fig,ax = plt.subplots(nrows = 4, ncols = 2, figsize = (9,14))
ax = ax.flat

for i,col in enumerate(cols_to_plot):
    df_class = data_eda[col].value_counts().to_frame()
    labels = df_class.index
    values = df_class.iloc[:,0].to_list()
    ax[i].pie(x = values, labels = labels, autopct=autopct_fun(values), shadow = True, textprops = {'color':'white', 'fontsize':10, 'fontweight':'bold'})
    ax[i].legend(labels)
    ax[i].set_title(col, fontsize = 14, fontweight = "bold", color = "black")
    ax[i].axis('equal')

fig.delaxes(ax = ax[7])
fig.tight_layout()
fig.show()

使用了 Matplotlib 的 pie 函数，通过循环遍历列，绘制了每个列的饼图。autopct_fun 函数定义了百分比标签的显示方式。

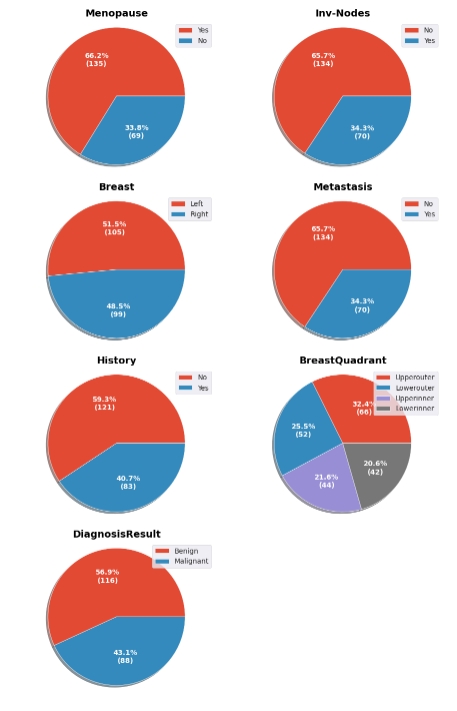
目标变量“DiagnosisResult”不平衡，在选择要评估的指标时必须考虑到这一点。

df_year = data_eda['Year'].astype(int).astype(str).value_counts().to_frame().sort_index()
labels = df_year.index
values = df_year.iloc[:,0]

fig,ax = plt.subplots(figsize = (5,3.2))
rects = ax.bar(labels, values)

def autolabel(rects):
    for rect in rects:
        height = rect.get_height()
        ax.annotate(text = height, 
                    xy = (rect.get_x() + rect.get_width()/2, height), 
                    xytext = (0,3), 
                    textcoords = 'offset points', 
                    ha = 'center', 
                    va = 'bottom')
autolabel(rects)
ax.set_title("Number of people detected with cancer in 2019 and 2020", fontsize = 8, fontweight = "bold", color = "black")
fig.show()

使用了 Matplotlib 的 bar 函数来创建柱状图，并通过 autolabel 函数在每个柱子上标注数值。展示了在2019年和2020年被检测出患有癌症的人数。

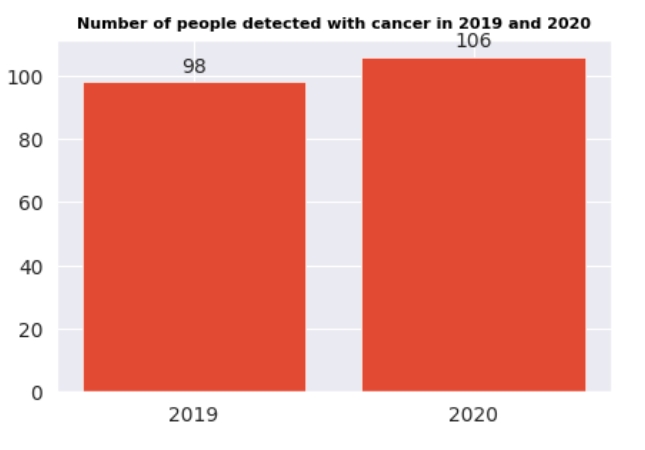
双变量分析

matrix_df = pps.matrix(data_eda)[['x', 'y', 'ppscore']].pivot(columns='x', index='y', values='ppscore')

plt.figure(figsize = (10,8))
sns.heatmap(matrix_df, vmin=0, vmax=1, cmap="coolwarm", linewidths=0.5, annot=True)
plt.title("Predictive Power Score (PPS)", fontsize = 20, fontweight = 'bold', color = 'black')
plt.show()

生成 Predictive Power Score (PPS) 矩阵的热力图，展示了各个变量之间的预测能力。使用了 PPS 库的 matrix 函数来计算变量之间的 Predictive Power Score，并通过 Seaborn 的 heatmap 函数绘制了热力图。

年龄与肿瘤大小(cm)

# Age vs TumorSize(cm)
g = sns.jointplot(data_eda, x = 'Age', y = 'TumorSize(cm)',kind = "reg", height = 4, joint_kws = {'color':'blue'})
g.fig.show()

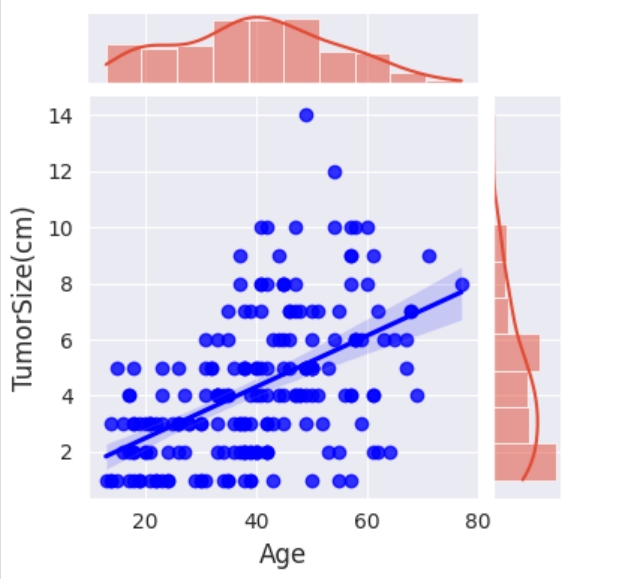
绘制 ‘Age’ 和 ‘TumorSize(cm)’ 两列之间的关系图，包括散点图和线性回归拟合线。使用了 Seaborn 库的 jointplot 函数，通过指定 kind="reg" 参数，生成了散点图和带有线性回归拟合线的关系图。

# 我们将使用 Spearman 相关性，因为这两个变量都不是来自正态分布的总体。
pg.corr(x = data_eda['TumorSize(cm)'], y = data_eda['Age'], method = "spearman")

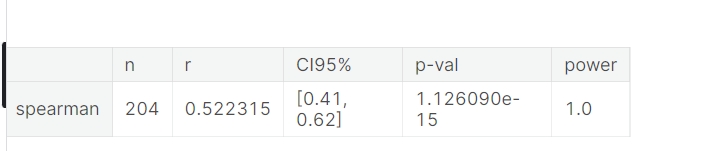
肿瘤大小（cm）与诊断结果

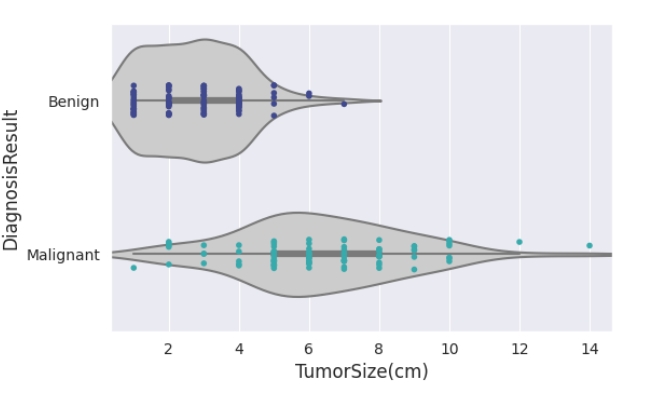
fig,ax = plt.subplots(figsize = (6,3.7))
sns.violinplot(data_eda, x = 'TumorSize(cm)', y = 'DiagnosisResult', color = '.8', ax = ax)
sns.stripplot(data_eda, x = 'TumorSize(cm)', y = 'DiagnosisResult', palette = 'mako', ax = ax, size = 4)
fig.show()

绘制小提琴图和散点图。使用了 Seaborn 库的 violinplot 函数绘制小提琴图，显示了 ‘TumorSize(cm)’ 对 ‘DiagnosisResult’ 的分布情况，并使用 stripplot 函数绘制了散点图，展示了每个数据点的位置。

data_eda.groupby('DiagnosisResult')['TumorSize(cm)'].describe()

计算 ‘DiagnosisResult’ 列的每个类别下 ‘TumorSize(cm)’ 列的描述性统计信息，包括均值、标准差、最小值、25% 分位数、中位数（50% 分位数）、75% 分位数和最大值。

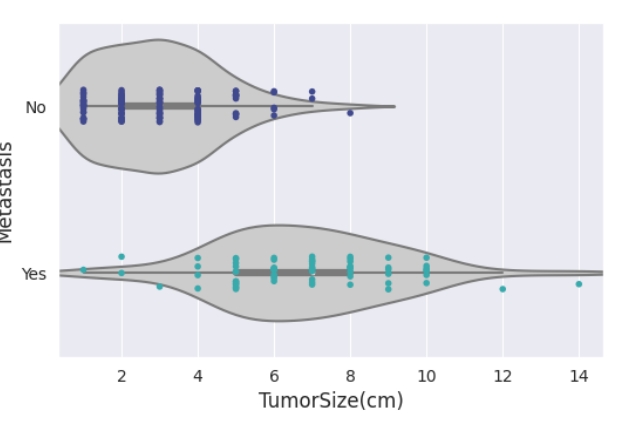
肿瘤大小（cm）与转移

fig,ax = plt.subplots(figsize = (6,3.7))
sns.violinplot(data_eda, x = 'TumorSize(cm)', y = 'Metastasis', color = '.8', ax = ax)
sns.stripplot(data_eda, x = 'TumorSize(cm)', y = 'Metastasis', palette = 'mako', ax = ax, size = 4)
fig.show()

data_eda.groupby('Metastasis')['TumorSize(cm)'].describe()

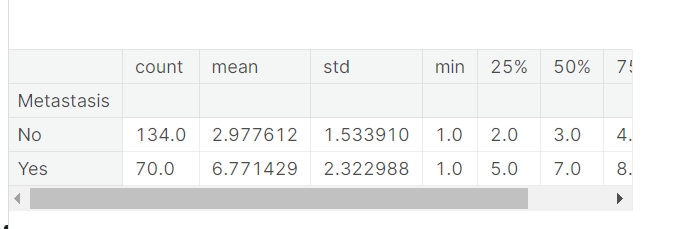
多元分析

g = sns.jointplot(data_eda, x = 'Age', y = 'TumorSize(cm)', hue = 'DiagnosisResult',height = 4)
g.fig.show()

使用 Seaborn 库的 jointplot 函数，绘制 ‘Age’ 和 ‘TumorSize(cm)’ 之间的关系图，并使用颜色（hue）区分 ‘DiagnosisResult’ 的不同类别。

g = sns.jointplot(data_eda, x = 'Age', y = 'TumorSize(cm)', hue = 'Metastasis', height = 4)
g.fig.show()

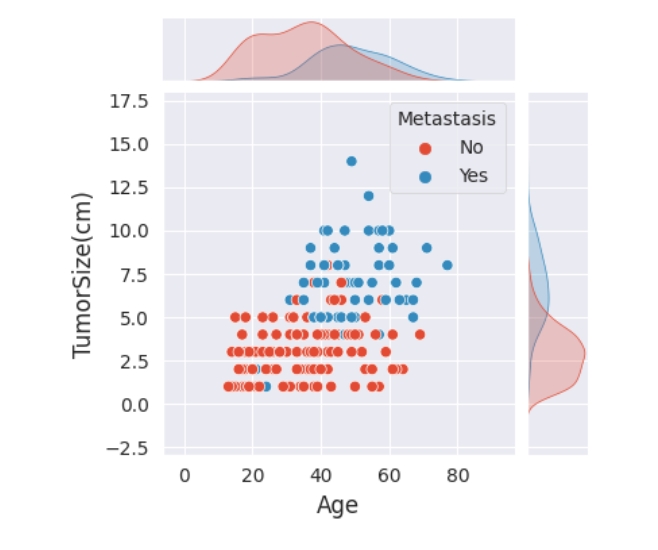
6.预处理

将我们的数据集分成目标变量和特征。

X = data.drop('DiagnosisResult', axis = 1)
y = data['DiagnosisResult']

创建字典来映射目标变量

label2id = {'Benign':0., 'Malignant':1.}

y = y.map(label2id)

分为训练和测试。

SEED = 42

X_train, X_test, y_train, y_test = train_test_split(X, 
                                                    y, 
                                                    test_size = 0.3, 
                                                    random_state = SEED)

y_train.value_counts()

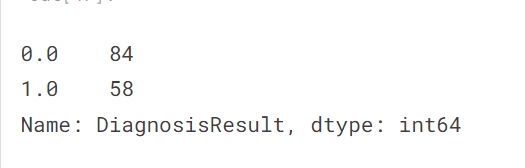
y_test.value_counts()

我们选择要应用某种类型转换的变量。

categorical_cols = ['Year', 'Breast', 'BreastQuadrant']
numerical_cols = ['Age', 'TumorSize(cm)']

preprocessor = ColumnTransformer([('scaler', PowerTransformer(), numerical_cols),
                                  ('ohe', OneHotEncoder(drop = 'first', sparse_output = False, handle_unknown = 'ignore'), categorical_cols)], 
                                 remainder = 'passthrough', verbose_feature_names_out = False).set_output(transform = 'pandas')

X_train_prep = preprocessor.fit_transform(X_train)
X_test_prep = preprocessor.transform(X_test)

7.模型

我们为 XGBClassifier 定义 scale_pos_weight 来处理类别不平衡。

scale_pos_weight = Counter(y_train)[0] / Counter(y_train)[1]
scale_pos_weight

我们定义候选模型，选择最能概括的模型。

clf1 = LogisticRegression(class_weight = 'balanced', random_state = SEED, n_jobs = -1, max_iter = 1000)
clf2 = RandomForestClassifier(random_state = SEED, n_jobs = -1)
clf3 = ExtraTreesClassifier(bootstrap = True, class_weight = 'balanced', n_jobs = -1, random_state = SEED)
clf4 = XGBClassifier(scale_pos_weight = scale_pos_weight, random_state = SEED, n_jobs = -1)
clf5 = LGBMClassifier(class_weight = 'balanced', random_state = SEED, n_jobs = -1)
clf6 = CatBoostClassifier(auto_class_weights = 'SqrtBalanced', random_state = SEED, verbose = 0)
clf7 = SVC(probability = True, class_weight = 'balanced', random_state = SEED)

MODELS = [clf1, clf2, clf3, clf4, clf5, clf6, clf7]

训练

accuracy_train = {}
accuracy_test = {}

for model in tqdm(MODELS):
    name = type(model).__name__
    model.fit(X_train_prep, y_train)
    y_pred_train = model.predict(X_train_prep)
    y_pred_test = model.predict(X_test_prep)
    accuracy_train[name] = balanced_accuracy_score(y_train, y_pred_train)
    accuracy_test[name] = balanced_accuracy_score(y_test, y_pred_test)
    print(f'* {name} finished.')

逻辑回归完成。

随机森林分类器完成。

ExtraTreesClassifier 完成。

XGBClassifier 完成。

LGBM分类器完成。

CatBoostClassifier 完成。

SVC 完成。

metric_train = pd.DataFrame.from_dict(accuracy_train, orient = 'index')
metric_train = metric_train.rename(columns = {0:'Train'})

metric_test = pd.DataFrame.from_dict(accuracy_test, orient = 'index')
metric_test = metric_test.rename(columns = {0:'Test'})

fig,ax = plt.subplots(figsize = (20,5))

labels = metric_train.index.to_list()
values_train = metric_train.iloc[:,0].to_list()
values_test = metric_test.iloc[:,0].to_list()
x = np.arange(len(labels))
width = 0.35

rects1 = ax.bar(x = x - width/2, height = values_train, width = width, label = 'Train')
rects2 = ax.bar(x = x + width/2, height = values_test, width = width, label = 'Test')


def autolabel(rects):
    for rect in rects:
        height = rect.get_height()
        ax.annotate(text = f'{height:.4f}', 
                    xy = (rect.get_x() + rect.get_width()/2, height), 
                    xytext = (0,3), 
                    textcoords = "offset points", 
                    ha = "center", 
                    va = "bottom")
        
autolabel(rects1)
autolabel(rects2)
ax.legend()
ax.set_title("Metric of Performance: Balanced Accuracy", fontsize = 12, fontweight = "bold", color = "black")
ax.set_ylabel("score", fontsize = 8, fontweight = "bold", color = "black")
ax.set_xlabel("Models", fontsize = 8, fontweight = "bold", color = "black")
ax.set_xticks(x)
ax.set_xticklabels(labels)
fig.show()

概括性最好的模型是 LogisticRegression。

结尾

在技术的飞速发展中，乳腺癌预测不再只是医学领域的挑战，更是技术与医学交汇的精彩契合。通过本文所介绍的EDA和模型应用，我们深刻认识到数据科学在医学中的潜力。这不仅仅是一篇关于乳腺癌的技术博客，更是对于我们共同探索、理解和战胜疾病的见证。相信通过数据的洞察和模型的运用，我们能够为乳腺癌预测开辟新的视野，为早期治疗提供更加精准的方向，最终为患者的健康带来福音。