Python实现GEE嵌套协方差结构仿真模型(GEE算法)项目实战

说明：这是一个机器学习实战项目（附带数据+代码+文档+视频讲解），如需数据+代码+文档+视频讲解可以直接到文章最后获取。

1.项目背景

广义估计方程（Generalized Estimating Equations, GEE）是一种用于分析具有重复测量或者集群数据的统计方法。在社会学、医学、生物学等多个领域，研究对象的数据往往存在嵌套或群聚结构，即个体的数据不是独立的，而是隶属于某个群体或层级结构中。?

GEE 嵌套协方差结构仿真模型的概念是指在应用 GEE 方法时，考虑了数据中的这种依赖性，并通过特定的协方差结构来模拟和描述各个观测值之间的相关性。例如，在临床试验中，同一个病人在不同时间点的多次观察结果之间可能存在相关性；在教育研究中，来自同一班级的学生的成绩可能由于共享班级效应而相互关联。

在 GEE 中，虽然关注的是参数的边际效应（即条件均值），但其核心是构造了一种有效的迭代算法来估计这些参数，同时考虑到因变量间的相关性结构。嵌套协方差结构通常包括但不限于交换able结构（如独立同分布）、自相关结构（如AR(1)过程）、 Toeplitz 结构、无条件异方差结构等。

简而言之，GEE 嵌套协方差结构仿真模型是一个灵活且强大的工具，能够处理不同类型的相关数据并提供对固定效应参数稳健且一致的估计，即使在数据不完全服从经典线性模型假设的情况下也能得到可靠的推断。

本项目通过GEE算法来构建嵌套协方差结构仿真模型。?

2.数据获取

本次建模数据来源于网络(本项目撰写人整理而成)，数据项统计如下：

编号	变量名称	描述
1	x0
2	x1
3	x2
4	x3
5	x4
6	y	因变量
7	groups_ix
8	level1_ix
9	level2_ix

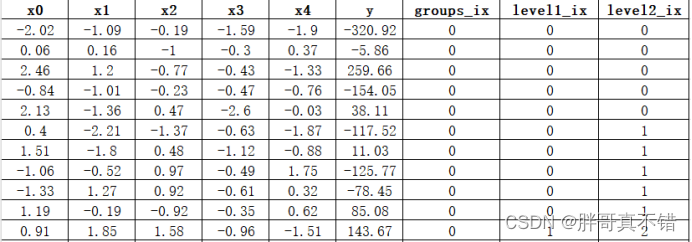
数据详情如下(部分展示)：

3.数据预处理

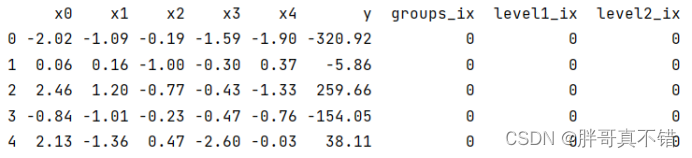
3.1?用Pandas工具查看数据

使用Pandas工具的head()方法查看前五行数据：

关键代码：

3.2 数据缺失查看

使用Pandas工具的info()方法查看数据信息：

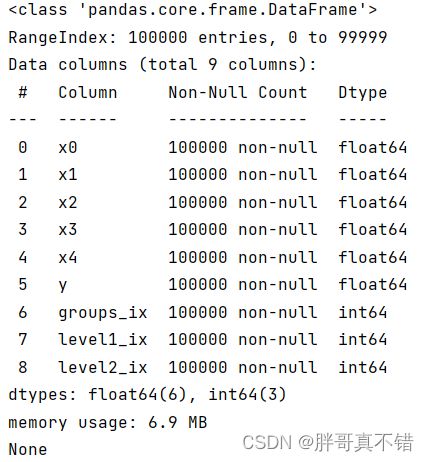
从上图可以看到，总共有9个变量，数据中无缺失值，共100000条数据。

关键代码：

3.3?数据描述性统计

通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。

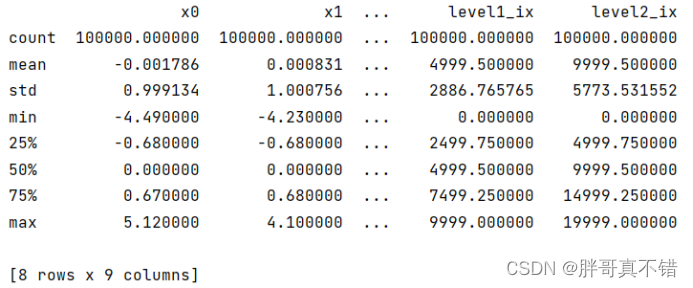
关键代码如下：

4.探索性数据分析

4.1?y变量直方图

用Matplotlib工具的hist()方法绘制直方图：

???

从上图可以看到，y变量主要集中在-400~400之间。

4.2 相关性分析

?????

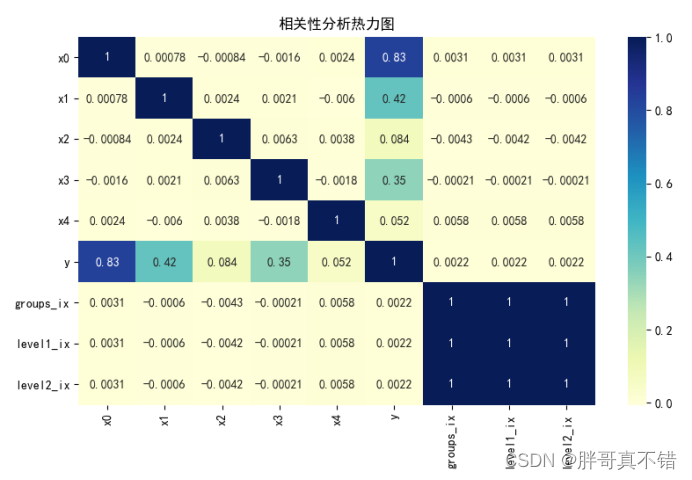从上图中可以看到，数值越大相关性越强，正值是正相关、负值是负相关。

5.构建GEE模型

主要使用GEE算法，用于目标回归。

5.1 构建模型

编号	模型名称	参数
1	GEE模型	cov_struct=cs
2		dep_data=dep_fml
3		groups="groups_ix"

5.2?模型协方差摘要信息

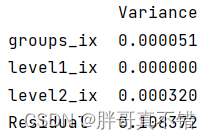
5.3?模型摘要信息

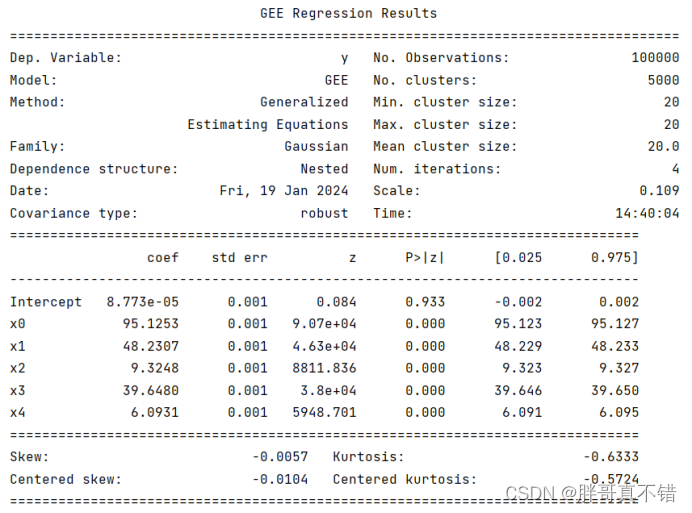
6.模型评估

6.1?评估指标及结果

评估指标主要包括可解释方差值、平均绝对误差、均方误差、R方值等等。?

模型名称	指标名称	指标值
测试集
GEE模型	??R方	1.0
	均方误差	0.1087
	可解释方差值	1.0
	平均绝对误差	0.273

从上表可以看出，R方为1.0，说明模型效果较好。

关键代码如下：

6.2?真实值与预测值对比图

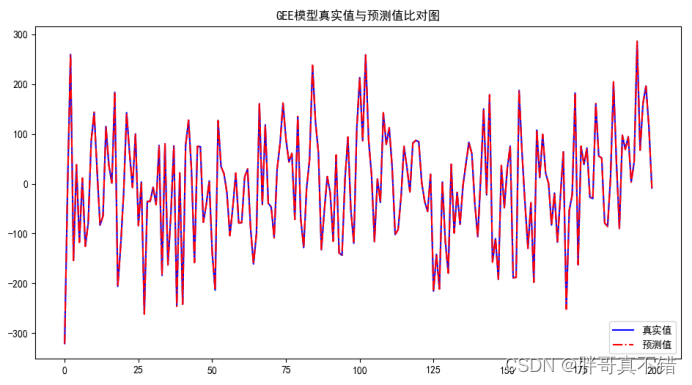
从上图可以看出真实值和预测值波动基本一致。

7.结论与展望

综上所述，本文采用了GEE算法来构建嵌套协方差结构仿真模型，最终证明了我们提出的模型效果良好。此模型可用于日常产品的预测。??

# 本次机器学习项目实战所需的资料，项目资源如下：
 
# 项目说明：
 
# 获取方式一：
 
# 项目实战合集导航：
 
https://docs.qq.com/sheet/DTVd0Y2NNQUlWcmd6?tab=BB08J2
 
# 获取方式二：

链接：https://pan.baidu.com/s/11HGesPKvqsUv-rCmjtHMCA 
提取码：hvv5