文章解读与仿真程序复现思路——高电压技术EI\CSCD\北大核心《计及能源自洽率和共享氢储能的电-氢-交通耦合配电网低碳经济运行》

这个标题涉及到电-氢-交通耦合配电网的运行，主要考虑到两个方面的因素，即"能源自洽率"和"共享氢储能"，并以此为基础来实现低碳经济运行。下面对标题中的关键术语进行解读：

1. 电-氢-交通耦合配电网：

   • 电-氢耦合：?表示电力和氢能源之间的相互关系。通常涉及电力系统将电能转化为氢能的过程，例如通过电解水制取氢气。
   • 交通耦合：?暗示了交通运输系统与电能和氢能的关联。这可能包括使用氢燃料电池驱动的交通工具，如氢燃料电池汽车、氢燃料电池公交车等。

2. 能源自洽率：

   • 能源自洽：?意味着系统内部的能源流动和利用是相对封闭的，尽量减少对外部能源的依赖。在这种上下文中，可能指的是通过内部能源循环，例如将可再生能源通过电解水生成氢，然后在需要时再将氢转化为电能。

3. 共享氢储能：

   • 氢储能：?表示氢气被用作储能媒介，以平衡电力系统中的不稳定性，例如储存电力过剩的能量。
   • 共享：?可能指多个能源系统或使用者之间共同利用同一储能系统，以提高整体效率。

4. 低碳经济运行：

   • 低碳：?指的是减少温室气体排放，采用更清洁、更可再生的能源，以降低对气候的不良影响。
   • 经济运行：?强调通过综合考虑经济效益和环境效益，实现系统的可持续运行。

因此，整个标题的含义可能是在电-氢-交通耦合的配电网系统中，通过最大化能源自洽率和共享氢储能，以实现低碳经济运行。这可能涉及到高效能源转换技术、氢能源的储存与分配系统、交通运输的清洁能源应用等方面的研究和优化。

摘要：新型储能的多元化发展促进了能源资源的优化配置和高水平就地消纳，本文提出了一种计及能源自洽率和共享氢储能（Shared Hydrogen Storage，SHS）的配电网低碳经济调度方法。首先，设计了包含电负荷-氢负荷的氢燃料电池车（Hydrogen Fuel Cell Vehicle，HFCV）交通网与新能源配电网双向耦合架构。在此基础上，以提高能源自洽率、降低碳排放成本为优化目标，综合考虑配电网、交通网、氢储能系统的运行约束条件以及短期氢储能（Short-term Hydrogen Storage，STHS）、SHS服务，建立了电-氢-交通耦合配电网的低碳经济优化调度模型，并给出了基于精英遗传算法(Elitist Strategy Genetic Algorithm，ESGA)的求解方法。最后，通过算例仿真验证了所提方法对于提升电-氢-交通耦合网络能源自洽率和降低碳排放成本的可行性和有效性。

这段摘要介绍了一种新型储能多元化发展的背景下，促进能源资源优化配置和高水平就地消纳的方法。具体而言，文中提出了一种电-氢-交通耦合配电网的低碳经济调度方法，其中考虑了能源自洽率和共享氢储能。

以下是对摘要的详细解读：

1. 储能多元化发展：

   • 指的是各种新型储能技术的不断发展和应用，有助于更有效地配置能源资源，并实现高水平的就地能源消纳。这反映了对储能领域多样性的关注。

2. 能源资源的优化配置和高水平就地消纳：

   • 表明新型储能的发展有助于更灵活地配置能源资源，以及在能源产生的地方更直接地利用这些能源，提高了就地消纳的水平。

3. 能源自洽率和共享氢储能：

   • 强调了两个关键概念。能源自洽率表示系统内能源循环的封闭程度，而共享氢储能则可能指多个系统或使用者之间共同使用氢气储能系统。

4. 配电网低碳经济调度方法：

   • 提出了一种优化电-氢-交通耦合配电网运行的方法，以实现低碳经济。这包括对配电网、交通网和氢储能系统的综合考虑。

5. 双向耦合架构：

   • 设计了包含电负荷-氢负荷的氢燃料电池车交通网与新能源配电网双向耦合架构，强调了交通和电力系统之间的相互影响。

6. 优化目标：

   • 以提高能源自洽率和降低碳排放成本为优化目标，显示了在优化运行中考虑了经济和环境因素。

7. 调度模型和求解方法：

   • 提到了建立了电-氢-交通耦合配电网的低碳经济优化调度模型，并采用了精英遗传算法（ESGA）进行求解，说明了解决这一复杂问题的方法。

8. 仿真验证：

   • 通过算例仿真验证了该方法对提升电-氢-交通耦合网络能源自洽率和降低碳排放成本的可行性和有效性，强调了提出方法的实际应用潜力。

综合而言，该研究旨在推动电-氢-交通耦合系统的可持续发展，通过细致考虑各种约束条件和服务，以实现低碳经济运行。

关键词:能源自治率: 电氢交通耦合;新型储能;共享氢储能;短期氢储能;

1. 能源自治率（Energy Self-Sufficiency）：

   • 指一个系统或社区在能源方面自给自足的程度，即在其运行中所需的能源几乎全部来自于内部产生或利用。较高的能源自治率意味着依赖外部能源供应的程度更低。在电氢交通耦合系统中，这可能指系统在能源方面更独立并自足，减少了对传统能源来源的依赖。

2. 电氢交通耦合（Electric-Hydrogen Transportation Integration）：

   • 指将电力系统和氢能系统相互耦合，以促进交通领域的能源转型。这意味着在交通运输中，特别是车辆方面，使用电力和氢能作为能源的整合和共享，可能是通过氢燃料电池车等方式实现的。

3. 新型储能（New Energy Storage）：

   • 指针对能源储存和释放进行创新的新技术或系统。这些新型储能技术可能包括但不限于针对电力的储能，例如电池技术的改进，以及利用氢气储能系统等。

4. 共享氢储能（Shared Hydrogen Storage）：

   • 指多个系统或使用者共同利用的氢气储能系统。这可能涉及多个能源系统之间的共享资源，以及通过共享储能系统提供灵活性和可靠性。

5. 短期氢储能（Short-term Hydrogen Storage）：

   • 指在短期内存储和释放氢气的系统。这可能是为了在能源需求波动时提供即时的氢气储备，以平衡能源供应和需求之间的差异。

这些概念的整合可能代表着一种发展方向，旨在通过创新的储能技术和系统集成，提高能源自治率，促进电氢交通耦合，实现共享和更有效地管理短期氢储能，以便更灵活、可持续地利用能源。

仿真算例：

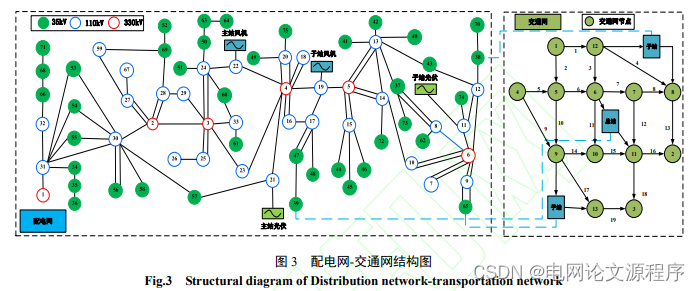
本算例以青海省海东市为例进行分析，在配 电网，主站光伏接入节点 21，子站光伏接入节点 11，主站风机接入节点 22，子站风机接入节点 19。 在交通网，设计一座总站，两座子站，通过加氢 站实现耦合，其配电网-交通网耦合情况如图 3 所 示。 电-氢-交通耦合配电网算例中加氢总站设有 STHS 和 SHS。加氢子站只有 STHS，即加氢子站 不能向加氢总站运输氢能，而且加氢子站之间也 无法做氢能互济。若风光分布式能源余电制氢无 法满足氢负荷需求，首先由加氢站 STHS 补足，如果仍存在氢能缺额，则由拖车调用加氢总站的 SHS。 算例以一天 24h 为调度周期，单位调度时间 为 15 分钟，风光分布式能源出力曲线如图 4（a） 所示，电负荷曲线如图 4（b）所示。氢负荷曲线 如图 4（c）所示，加氢总站单日 HFCV 上限为 1000 辆，加氢子站 1 和加氢子站 2 单日 HFCV 上限均为 600 辆。该地区实时电价和氢价如图 4（d） 所示。加氢总站氢储设备总容量为 4000kg，加氢 子站氢储系统总容量为 2000kg。氢能拖车运输时 间为下午 4:00。配电网从上一级电网购电 1kW·h 产生 CO2 0.96kg，制氢气 25.2 克，其他基础参数 见表 1。

仿真程序复现思路：

仿真的复现思路可以分为以下步骤：

1. 建立模型：

   • 根据描述，首先需要建立电-氢-交通耦合配电网的数学模型。这可能包括配电网和交通网的节点、线路参数，光伏和风机的发电模型，氢储设备的容量等。同时，需要考虑实时电价和氢价对系统的影响。

2. 精英遗传算法设计：

   • 为了解决问题，采用精英遗传算法进行优化。该算法包括个体的编码、初始化种群、适应度函数的定义、交叉和变异操作等。适应度函数应该考虑电-氢-交通耦合系统中各个部分的运行状态，满足氢负荷需求，最小化系统运行成本等。

3. 仿真调度周期：

   • 根据算例的设定，仿真以一天24小时为调度周期，单位调度时间为15分钟。在每个调度周期内，需要更新系统状态，计算能源产生和消耗情况，以及进行优化算法的操作。

4. 优化目标：

   • 优化目标可能包括最小化系统总成本（包括电价、氢价、运输成本等），最大化能源自治率，确保氢负荷得到满足，以及保证加氢站和子站的运行在规定上限内等。

5. 模拟实时电价和氢价：

   • 模拟实时电价和氢价的变化对系统运行的影响。这可以通过使用仿真周期内的电价和氢价曲线来模拟。

6. 结果分析：

   • 在仿真结束后，对优化算法得到的结果进行分析。可以绘制各个节点的能源产生和消耗曲线，观察系统在不同条件下的运行情况。

以下是简化的 Python 伪代码，用于表示精英遗传算法的一般框架。这只是一个简单的示例，实际实现可能需要更详细的设计和调优。

import numpy as np

# 模型参数
num_generations = 50
population_size = 20
mutation_rate = 0.1
num_elites = 2

# 模型中的节点和参数
# 这里仅是一个示例，实际情况可能需要更多的节点和参数
nodes = {
    'main_station_pv': 21,
    'sub_station_pv': 11,
    'main_station_wind': 22,
    'sub_station_wind': 19,
    # 其他节点...
}

# 电-氢-交通耦合系统的模型类
class EnergySystemModel:
    def __init__(self):
        # 初始化模型参数
        # ...

    def simulate(self, strategy):
        # 模拟系统运行，根据给定的策略
        # ...

# 遗传算法的操作函数
def initialize_population(population_size):
    # 随机初始化种群
    return np.random.rand(population_size, len(nodes))

def calculate_fitness(individual):
    # 计算适应度函数
    model = EnergySystemModel()
    return model.simulate(individual)

def crossover(parent1, parent2):
    # 交叉操作，这里使用单点交叉
    crossover_point = np.random.randint(len(parent1))
    child1 = np.concatenate((parent1[:crossover_point], parent2[crossover_point:]))
    child2 = np.concatenate((parent2[:crossover_point], parent1[crossover_point:]))
    return child1, child2

def mutate(individual):
    # 变异操作，这里使用随机变异
    mutation_mask = np.random.rand(len(individual)) < mutation_rate
    individual[mutation_mask] = np.random.rand(np.sum(mutation_mask))
    return individual

def elitism_selection(population, fitness_values, num_elites=2):
    # 筛选精英个体
    elite_indices = np.argsort(fitness_values)[:num_elites]
    return population[elite_indices]

# 主要迭代过程
population = initialize_population(population_size)

for generation in range(num_generations):
    fitness_values = np.array([calculate_fitness(individual) for individual in population])

    elites = elitism_selection(population, fitness_values, num_elites)

    new_population = []

    for i in range(population_size - num_elites):
        parent1, parent2 = population[np.random.choice(population_size, size=2, replace=False)]
        child1, child2 = crossover(parent1, parent2)
        child1 = mutate(child1)
        child2 = mutate(child2)
        new_population.extend([child1, child2])

    population = np.vstack([elites, new_population])

# 最终结果分析
best_solution_index = np.argmin(fitness_values)
best_solution = population[best_solution_index]
best_fitness = fitness_values[best_solution_index]
print(f"Best Solution: {best_solution}")
print(f"Best Fitness: {best_fitness}")

在这个示例中，EnergySystemModel类代表了电-氢-交通耦合系统的模型，simulate函数用于模拟系统运行。遗传算法的初始化、交叉、变异、选择等操作都在代码中实现。请注意，这只是一个简化的例子，实际情况可能需要更多的细节和复杂性。