力扣刷题-二叉树-二叉搜索树中的搜索

700 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL。
例如，

在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回None。

思路

二叉搜索树是一个有序树：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉搜索树

这就决定了，二叉搜索树，递归遍历和迭代遍历和普通二叉树都不一样。
本题，其实就是在二叉搜索树中搜索一个节点。那么我们来看看应该如何遍历。

递归

1. 确定递归函数的参数和返回值

递归函数的参数传入的就是根节点和要搜索的数值，返回的就是以这个搜索数值所在的节点。

2. 确定终止条件

如果root为空，或者找到这个数值了，就返回root节点。

3. 确定单层递归的逻辑

看看二叉搜索树的单层递归逻辑有何不同。
因为二叉搜索树的节点是有序的，所以可以有方向的去搜索。
如果root->val > val，搜索左子树，如果root->val < val，就搜索右子树，最后如果都没有搜索到，就返回None。

# 学习二叉搜索树的特性
class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

# 1. 递归法 
class Solution(object):
    def searchBST(self, root, val): # 1. 确定递归函数参数是传入根节点还要给定值 返回值为节点类型
        """
        :type root: TreeNode
        :type val: int
        :rtype: TreeNode
        """
        # 2. 确定终止条件 树为空 或 找到这个值 都返回 root 注意 root是递归迭代的 用root代表树
        if not root or root.val == val:
            return root
        # 3. 单层逻辑 root.val > val  与 root.val < val 进行比较
        if root.val > val:
            result = self.searchBST(root.left, val) # 需要用一个变量来接收返回值
        if root.val < val:
            result = self.searchBST(root.right, val)
        return result

迭代法

一提到二叉树遍历的迭代法，可能立刻想起使用栈来模拟深度遍历，使用队列来模拟广度遍历。
对于二叉搜索树可就不一样了，因为二叉搜索树的特殊性，也就是节点的有序性，可以不使用辅助栈或者队列就可以写出迭代法。
对于一般二叉树，递归过程中还有回溯的过程，例如走一个左方向的分支走到头了，那么要调头，在走右分支。
而对于二叉搜索树，不需要回溯的过程，因为节点的有序性就帮我们确定了搜索的方向。
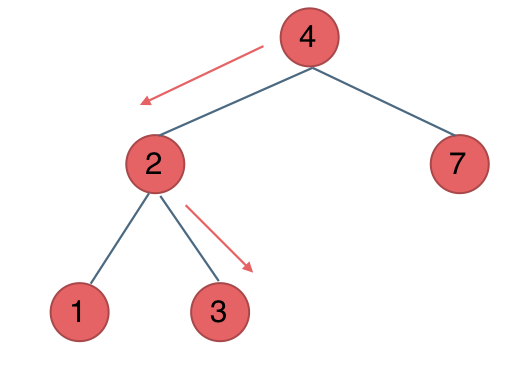
例如要搜索元素为3的节点，我们不需要搜索其他节点，也不需要做回溯，查找的路径已经规划好了。
中间节点如果大于3就向左走，如果小于3就向右走，如图：

        
# 2. 迭代法 注意二叉搜索树的特性
class Solution(object):
    def searchBST(self, root, val):
        while root: # 循环(遍历)
            if root.val > val:
                root = root.left
            elif root.val < val:
                root = root.right
            else:
                return root
        return None

总结

本篇介绍了二叉搜索树的遍历方式，因为二叉搜索树的有序性，遍历的时候要比普通二叉树简单很多。
但是很容易忽略二叉搜索树的特性，所以写出遍历的代码就未必真的简单了。
所以针对二叉搜索树的题目，一样要利用其特性。

参考：
https://www.programmercarl.com/0700.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E6%90%9C%E7%B4%A2.html#%E6%80%9D%E8%B7%AF