【论文阅读】O’Reach: Even Faster Reachability in Large Graphs

Hanauer K, Schulz C, Trummer J. O’reach: Even faster reachability in large graphs[J]. ACM Journal of Experimental Algorithmics, 2022, 27: 1-27.

Abstract

计算机科学中最基本的问题之一是可达性问题：给定一个有向图和两个顶点s和t，s可以通过一条路径到达t吗？我们重新讨论现有的技术，并将它们与新的方法结合起来，使用线性大小的可达性索引在恒定的时间内支持大部分可达性查询。我们的新算法O‘Reach可以很容易地与以前开发的问题解决方案相结合，或者独立运行。
在一项详细的实验研究中，我们比较了各种算法的索引构建和查询时间，以及它们在不同实例集上的内存占用。我们的实验表明，查询性能通常不仅强烈地依赖于图的类型，而且还取决于结果，即可达或不可达。此外，我们还表明，在几乎所有情况下，以前的算法与新方法的结合都显著加快。令人惊讶的是，由于缓存效应，在空间上的更高投资并不一定会有回报：在预先计算的全可达性矩阵中，可达性查询通常可以比单个内存访问更快地被回答。

1 INTRODUCTION

图用于建模各种不同学科的问题设置。经常出现的一个自然问题是，图的一个顶点能否通过有向边路径到达另一个顶点。可达性可以在许多领域得到应用，如程序和数据流分析[24,25]、用户输入依赖分析[27]、XML查询处理[34]和更多的[40]。另一个突出的例子是由RDF/OWL数据组成的语义Web。这些图表通常都是非常巨大的、内容丰富的图表。在这里，可达性查询通常需要用来推断对象之间的关系。
对于可达性问题有两种直接的解决方案：第一种是在最坏情况下的O（m+）时间和O（+）空间中分别回答每个查询，例如宽度优先搜索（BFS）或深度优先搜索（DFS）。其次，我们可以在初始化步骤中预先计算一个完整的全对可达性矩阵，并在最坏情况常数时间内回答随后的所有查询。作为回报，这种方法的空间复杂度为O（n2），初始化时间为O（n·m），使用Floyd-警告算法[6,7,35]或依次在每个顶点开始一个图遍历。或者，初始化步骤可以通过快速矩阵乘法在O（nω）中执行，其中O（nω）是乘以两个n×n矩阵所需的时间（2≤ω < 2.38 [20]）。然而，随着图大小的增加，该方法的初始化时间和空间复杂度都变得不切实际。因此，我们努力寻找替代算法来降低这些复杂性，同时仍然提供快速的查询查找。
贡献。在本文中，我们研究了能够支持快速链查询的各种方法。所有这些算法都对图进行了某种预处理，然后利用收集到的数据及时回答可达性查询。基于简单的观察，我们提供了一种新的算法，O‘Reach，它可以在最先进的可达性算法相比，提高大量情况的查询时间，而牺牲一些额外的预计算时间和空间，或独立运行。此外，我们还表明，在几乎所有情况下，以前的算法与新方法的结合都显著加快。此外，我们还证明了各种算法的预期查询性能不仅取决于图的类型，而且还取决于成功查询的比率，即结果的可达性。令人惊讶的是，通过缓存效应和明显较小的内存占用，特别是不成功的可达性查询，可以比预先计算的可达性矩阵中的单个内存访问更快地得到回答。

2 PRELIMINARIES

术语和定义。设G =（V，E）是一个简单的有向图，具有顶点集V和边集E?V×V。像往常一样，n = |V |和m = |E|。一条边（u，v）在u处流出，在v处进入，u和v被称为相邻边。顶点u的出度度+(u)（内度度?(u))是它的传出（传入）边的数目。没有传入（传出）边缘的顶点称为源（接收器）。一个顶点u的外邻域N+(v)（内邻域N?(v)）是所有顶点v的集合，使得（u，v）∈E（（v，u）∈E）。一条边（u、v）的反面是一条边（v、u）=(u、v）R。图G的反向GR是通过保持G的顶点得到的，但将每条边（u，v）∈E用它的反向代替，即GR =（V，ER）。
一个顶点序列的= v0→···→vk = t，k≥0，这样对于每一对连续的顶点，vi→vi+1，（vi，vi+1）∈E，被称为s-t路径。如果存在这样的路径，就说s到达t，我们缩写→?，否则写→?。一个顶点u∈v的外可达性R+ (u) = {v | u→?v}（内可达性R?(u) = {v | v→?u}）是你可以到达（可以到达u）的所有顶点的集合。
G的弱连通分量（WCC）是最大的顶点C?V，使得G =（V，E∪ER）中的?u，v∈C： u→?v，即也使用边的反面。注意，如果两个顶点u，v位于不同的wcc中，那么u→?v和v→?u。G的强连通分量（SCC）表示最大的顶点S?V，使?u，v∈S： u→?v∧→?→?将G的每个SCC S收缩到一个顶点vS，称为其代表，同时保留不同SCC之间的边作为其对应代表之间的边，产生g的凝聚GC。我们用S (v)表示顶点v∈∈属于的SCC。当一个有向图G只有一个SCC时，它是强连通的，如果每个SCC是一个单例时，它是无环的，即，如果G有n个SCC。观察到G和GR具有完全相同的WCCs和SCCs，GC是一个有向无环图（DAG）。一个图的WCCs可以在O（n + m）时间内计算出来，例如，通过一个忽略边缘方向的BFS。一个图的SCCs也可以在线性时间[29]中计算出来。
DAG G的拓扑排序τ： V→n0是其顶点的总排序，使?（u，v）∈E： τ (u) < τ (v)。请注意，G的拓扑顺序并不一定是唯一的，也就是说，可能有多个不同的拓扑顺序。对于一个顶点u∈V，正向拓扑水平F (u) = minτ τ (u)，即∈的所有拓扑顺序τ中τ (u)的最小值。因此，当且仅当u是一个源时，F (u) = 0。当且仅当u是一个汇时，u∈V的反向拓扑水平B (u)是u相对于GR和B (u) = 0的拓扑水平。一个拓扑顺序，以及正向和向后的拓扑水平，可以在线性时间[6,19,30]中计算，也请参见第4节。
对于一对节点s，t∈V的可达性查询（s，t），如果s→?t则用true回答，否则为负，用false回答。基本上，Query（v，v）总是正确的，这就是为什么我们从这里开始只考虑不同顶点st∈V之间的非平凡查询。设P (N)表示G的所有正（负）非平凡查询的集合，即所有（s，t）∈V×V，st的集合，这样Query（s，t）是正（负）。G中的可达性ρ是所有非平凡查询中正查询的比率，即ρ=n（|P|n?1）。注意，由于对非平凡查询的限制，1 0 个≤ρ≤1。本文研究的可达性问题包括在给定的输入图上回答任意顶点对的可达性查询序列。
基本的观察结果。关于处理图G中任意一对顶点t∈V的可达性查询（s，t），以下基本观察是直接的，并且在[22]的其他地方也被注意到：
（B1）如果s是尾或t是源，那么s/→?t。
（B2）如果s和t属于G的不同WCC，则s/→?t。
（B3）如果s和t属于G的同一SCC，则为s→?t。
（B4）如果τ（S (t)）< τ（S (s)）对于GC的任何拓扑排序τ，则s/→?t。
如上所述，观测（B2）和（B3）所需的预计算可以在O（n + m）时间内执行。然而，请注意，观察（B3）和（B4）一起等同于询问是否s→?t：如果s→?t且τ（S (s)）≠τ（S (t)），那么对于每个拓扑排序τ，τ（S (s)）<τ（S (t)）。否则，如果是s/→?t，一个拓扑排序τ（S (t)）< τ（S (s)）可以通过拓扑排序GCτ∪{（SS (t)，S(s)）}来计算。因此，观测（B4）所需的预先计算将已经需要解决所有顶点对的可达性问题。此外，一个DAG可以有指数级的许多不同的拓扑顺序。因此，采用了较弱的形式，如以下[22,38,39]（参见第4节）：
（B5）如果F（S (t)）< F（S (s)）w. r. t。GC，然后是s/→?t。
（B6）如果B (S(s) < B（S(t)）w. r. t。GC，然后是s/→?t。
假设。根据在前面的工作[3,22,38,39] (cf。第3节)，我们从这里开始只考虑dag上的可达性，并隐式地假设，如果有必要，已经计算了凝结，并应用了观测（B3）。为了更好的可读性，我们也放弃了S（·）的使用。

3 RELATED WORK

对可达性指标进行了大量的研究。现有的方法大致可以分为三类：传递闭包压缩[2,13-15,32,34]，基于可标记的算法[4,5,16,26,37]，以及修剪的搜索[18,22,28,31,33,36,38,39]。正如Merz和Sanders [22]所指出的，第一类为小型网络提供了非常好的查询时间，但不能很好地扩展到大型网络（这是这项工作的重点）。因此，我们不更仔细地考虑基于这种技术的方法。跳标记算法通常从存储在每个顶点的标签中构建路径。例如，在2跳标记中，每个顶点存储两个集合，其中包含它在给定的图和反向图中可以到达的顶点。然后可以将查询简化为集合交集问题。基于剪枝搜索的方法预先计算信息，通过剪枝搜索来加快查询速度。
由于它的体积，它不可能与以前的所有工作进行比较。我们主要遵循Merz和桑德斯[22]的方法，并重点关注最近的五项技术。最近的两种基于跳跃标记的方法是TF [3]和PPL [37]。在修剪搜索类别中，最新的三种方法分别是PReaCH [22]、IP [36]和BFL [28]。现在我们将更详细地介绍：
TF Cheng等人[3]的工作使用了一种称为拓扑折叠的数据结构。在凝聚DAG上，作者定义了一个拓扑结构，每次递归折叠一半得到。使用这种拓扑结构，作者创建了可以帮助快速回答可达性查询的标签。
PPL Yano等人[37]使用修剪的地标标记和修剪的路径标记作为其可达性查询的标签。一般来说，该方法遵循上述的2跳标记技术，为每个顶点v存储顶点集，并将查询简化为集合交集问题。他们的技术能够减少存储标签的大小，从而提高查询时间和空间消耗。
PReaCH Merz和Sanders [22]将最短路径查询的收缩层次[9,10]方法应用于可达性问题。该方法首先尝试通过使用剪枝和预先计算的信息来回答查询，如拓扑级别（观察（B5）和（B6）)。它采用并改进了GRAIL [38,39]的技术，在随后的实验中明显优于PReaCH。如果这些技术不能回答查询，PReaCH将使用计算的层次结构执行双向BFS，即，对于查询（s，t），BFS只考虑具有较大拓扑级别和沿CH的相邻顶点。总体方法简单，保证了线性空间和近线性预处理时间。
IP Wei等人[36]通过在标签上应用独立的排列来使用随机标记方法。与其他标记方法相反，IP检查集合包含，而不是集合交集。因此，IP试图通过检查至少一个顶点是否只包含在两个集合中的一个中来回答负查询，其中每个集合最多可以由kIP顶点组成。如果此测试失败，IP将检查另一个标签，该标签包含来自具有最大出度的hIP顶点的预先计算的可达性信息，否则将返回到DFS。
BFL Su等人[28]提出了一种基于IP的标记方法，但另外使用Bloom过滤器来存储和比较标签，然后用于回答负查询。作为参数，BFL接受sBFL和dBFL，其中sBFL表示为每个顶点存储的Bloom过滤器的长度，而dBFL控制假阳性率。默认情况下，dBFL = 10·sBFL。
表1包含了我们在第4节中介绍的新算法O‘Reach的时间和空间复杂度，以及本文中提到的所有算法，除了TF，其中描述理论复杂度的表达式本身体积庞大且相当复杂。

4 O’REACH: FASTER REACHABILITY VIA OBSERVATIONS

在本节中，我们提出了我们的新算法O‘Reach，它基于一组简单而强大的观察结果，使我们能够在恒定的时间内回答大部分的可达性查询，并将来自跳跃标记和修剪搜索的技术结合在一起。然而，与常规的跳点标记方法不同，它的初始化时间是线性的。此外，我们的算法可以通过多个参数进行配置，并且在最节省空间的配置中，索引只有38n字节，可以处理第5节中使用的所有实例，并使用所有特性。
概述在我们的算法中使用的跳跃标记技术是受到Hanauer等人[11]最近在动态图中实验中更快的可达性查询的实验结果的启发。这里的想法是基于一组所谓的支持顶点来加速可达性查询，对于这些顶点，显式地维护完整的外可达性和内可达性。这些信息用于三个简单的观察，允许在常定时间内回答匹配的查询。在我们的算法中，我们将这个想法转移到静态设置中。通过对拓扑顺序及其与DFS合并的新视角，我们进一步提高了在恒定时间内可回答查询的比例，从而提供了额外的可达性信息，并进一步增加了在恒定时间内可回答查询的比例。如果我们不能通过观察回答查询，我们可以回到剪枝双向BFS或现有算法之一。
下面，我们将切换顺序，首先深入讨论拓扑顺序，然后是我们对支持性顶点的自适应。对于这两个部分，考虑两个顶点s，t∈V和st的可达性查询（s，t）。

4.1 Extended Topological Orderings

考虑到拓扑顺序可以用来回答可达性查询完全为负的观察，我们首先研究如何在实践中最有效地使用观察（B4）。在我们深入研究这个主题之前，让我们简要回顾一些关于拓扑顺序和可达性的事实。
定理4.1。设N (τ)?N表示一个拓扑排序τ可以回答的负查询集合，即所有（s，t）∈N的集合，使τ (t) < τ (s)，并设ρ?(τ) = N（τ）/N为可回答的负查询比率。
(i)任何DAG的可达性最多为50%。在这种情况下，拓扑顺序是唯一的。
（ii）任何拓扑排序τ都证明了所有不同顶点对的50%之间的非可达性。因此，ρ?(τ)≥为50%。
（iii）同一DAG的每一个拓扑排序都可以通过观察（B4）回答所有负查询的相同比例，即对于两个拓扑排序τ，τ：ρ?(τ)=ρ?（τ）。
（iv）对于一个DAG的两种不同的拓扑顺序ττ，N (τ) N（τ）。
证明。设G是一个DAG。
(i) G是无环的，至少有一个拓扑顺序τ。然后，对于G的每条边（u，v），τ (u) < τ (v)，这意味着每个顶点u最多可以用τ (u) < τ (w)到达wu的所有那些顶点。因此，一个具有τ (u) =的顶点u最多可以到达n?i?1其他顶点（注意?≥0）。因此，G的可达性最多为n（n 1?1）n?1i=0（n?i?1）=1n（n?1）n?1j=0j=n（n?1）n（n?1）·2=1 2 。相反，假设G中的可达性为1 2 。然后，每个具有τ (u) =的顶点u恰好到达它之后的其他顶点，这意味着不存在具有τ(u) > τ (u)的其他拓扑排序τ。通过对i的归纳法，G的拓扑顺序是唯一的。
（ii）设τ是g的任意拓扑顺序。然后，每个用τ (u) = i的顶点u肯定可以用τ (v) < τ (u)到达这些顶点v。因此，τ见证了恰好是n个?1i=1i=n（n2?1）不同顶点对的非可达性。
（iii）由于观察结果（B4）完全对应于拓扑排序所见证的这些顶点对之间的非可达性，因此该主张直接来自（ii）。
（iv）作为ττ，，至少有一个i∈N0，即τ (u) = i = τ(v)和uv。让j = τ (v)。如果j > i，则τ见证的从v到另一个顶点的非能数超过τ，见证的数量，否则则落后于它。在这两种情况下，数字的差异立即意味着顶点对集合的差异，这证明了这一主张。
因此，寻找一个特别好的拓扑排序是没有意义的。相反，为了最大限度地利用观测（B4），我们需要拓扑顺序，其可回答的负查询集差异很大，这样它们的并集覆盖了N的很大一部分。注意，前向和向后拓扑级别都表示拓扑顺序集，这些拓扑顺序可以通过对按级别分组的块中的顶点进行排序，并任意排列每个块中的顶点来获得。多年来，人们提出了在线性时间内计算拓扑排序的不同算法[6,19,29]，Kahn算法[19]结合队列总是产生由前向拓扑层次表示的拓扑排序。因此，我们通过基于堆栈的方法来补充前向和后向拓扑水平，如在Kahn的算法[19]结合堆栈或Tarjan的基于dfs的算法[29]，用于计算图的SCCs，它作为副产品也产生凝聚的拓扑顺序。为了进一步多样化可回答的负查询集，我们在绑定的情况下，另外将顶点的处理顺序随机化，并在反向图上计算拓扑顺序，类似于后向拓扑层次。
接下来，我们将展示如何通过一个小的扩展，使用上面提到的基于堆栈的拓扑排序来额外回答正查询。为了保持描述的简洁，我们将重点关注Tarjan算法[29]，并将其简化为与获得DAG拓扑排序相关的部分。简而言之，该算法在任意顶点∈S开始DFS，其中?V是给定的顶点集。每当它访问一个顶点v时，它就将v标记为已访问的，并递归地访问其外邻域中所有未访问的顶点。返回时，它在拓扑排序中添加v。对S = V的循环确保访问所有顶点。请注意，尽管顶点是按DFS顺序访问的，但拓扑顺序不同于DFS编号，因为它是“从后到前”构造的，并且对应于根据每个顶点的完成时间进行的反向排序。
为了回答正查询，我们利用了一个不变量，即当访问一个顶点v时，所有从v可访问的未访问的顶点将在v提前之前进行拓扑排序。因此，v当然可以到达v之间的拓扑排序中的所有顶点，以及在访问v时位于拓扑排序前面的顶点w。设x表示最终拓扑排序中w之前的顶点，即从v递归到达的索引最大的顶点。对于用这种方式构造的拓扑有序τ，我们称τ (x)为v的高索引，并用τH (v)表示它。此外，v也可以到达w和顶点，如果某些顶点y，但是y之前已经被访问过了。因此，我们另外跟踪最大索引，即v所能达到的任何顶点的最大索引，并用τX (v)表示它。图1(a)展示了如何在伪代码中计算具有高指数和最大索引的扩展拓扑排序，并突出显示了我们的扩展。与Tarjan的原始版本[29]相比，运行时间不受我们的修改的影响，仍然在O（n + m）。

注意，马克斯和高指数收益率V的顺序：每个顶点访问递归地从v和顶点xτ(x)=τH(v)，包括，有相同的高指数v，和每个顶点的高指数在一个图组成的一个路径，例如，将n-1。特别是，max和高索引都不会形成DFS编号，而且在定义和使用上也与PReaCH中使用的DFS完成时间??不同，其中顶点v肯定可以到达DFS编号高达??的顶点，当然不能超过这个顶点。相反，v也可以到达比DFS自己的DFS数更小的顶点，这不能发生在拓扑顺序中。
如果在反向图上运行，它产生一个拓扑排序τ和高最大指数τH和τX，这样反转τ再次产生原始图的拓扑排序τ。此外，τL (v) ：= n?1?τH(v)是每个顶点v的低索引，它表示τ中肯定可以达到v的顶点的最小索引，即v的外可达性被内可达性所取代。类似地，τN (v) ：= n?1?τX(v)是τ中的一个最小索引，没有使用τ (u) < τN (v)的顶点u可以达到v。
下面的观察显示了如何使用这种扩展的拓扑顺序τ来回答正和负可达性查询：

回想一下，根据定义，τ (s)≤τH (s)≤τX (s)和τN (t)≤τL (t)≤τ (t)。图1(b)描述了三个扩展拓扑顺序的例子。与负查询相比，并不是每个扩展拓扑排序在回答正查询时都同样有效，它可以是任意坏的，如图1(b)左边（最坏）和中间（最好）的极端所示：
定理4.2。设P(τ)?P是一个扩展的拓扑顺序τ可以回答的正查询集，并设ρ+ (τ) = P（τ）/P是可回答的正查询比率。然后，0≤ρ+ (τ)≤1。
相反，扩展拓扑排序的有效性积极取决于范围的大小τ(v)τH(v)和τL(v)τ(v)，负的τH(v)τX(v)和τN(v)τL(v)]反过来取决于递归深度在建设和递归调用的顺序。如果在ExtendedTopSort中第4行对访问的第一个非递归调用总是有一个源作为其参数，即如果算法的参数S对应于所有源的集合，则前两个可以最大化。显然，这仍然保证了每个顶点都能被访问。
除了正向和向后拓扑级别，O‘Reach因此从源开始计算一组d扩展拓扑顺序，其中d是一个调优参数，其中d/2通过反图得到。然后，它将观测（B4）和观测（T1）-（T6）应用于所有扩展的拓扑排序。

4.2 Supportive Vertices

我们现在将展示如何在静态设置中应用和改进支持性顶点的思想。如果v可以到达和可以到达v、R+ (v)和R?(v)的顶点集已经预先计算，并且可以在次线性时间内执行成员查询，那么顶点v是支持的。然后，我们可以使用以下简单的观察结果[11]来回答可达性查询：
（S1）如果s∈R?(v)和t∈R+ (v)任何v∈V，那么s→?t。
（S2）如果s∈R+ (v)和t/∈R+ (v)任何v∈V，那么s/→?t。
（S3）如果s/∈R?（v）和t∈R?（v）任何v∈V，那么s/→?t。
为了应用这些观察结果，我们的算法在初始化阶段选择了一组k个支持的顶点。与原始使用场景的动态设置，图变化随着时间的推移，很难选择“好”支持顶点，可以帮助回答许多查询，静态设置留下进一步优化的空间：对观察（S1），我们认为支持顶点v“好”如果|R+(v)|·|R?(v)|很大，因为它最大化的可能性s∈R?(v)∧t∈R+ (v)。关于观察（S2）和（S3），我们期望一个“良好的”支持顶点分别有接近n2的外部或内部可达性集，即当|R+(v)|·|V\R+(v)|或|R?(v)|·|V\R?(v)|分别最大时。此外，为了增加总覆盖率和避免冗余，理想情况下，由两个不同的支持顶点覆盖的查询查询（s，t）集应该尽可能少地重叠。
O‘Reach采用一个参数k，指定要选择的支持性顶点的数量。直观地说，我们期望拓扑“中层”中的顶点比最终的顶点更好，因为它们的外适应能力和内适应能力（或非适应能力）可能更加平衡。此外，如果一个正向（向后）级别i上的所有顶点都是支持的，那么每个具有F(s)<<(t)（<）<<))的查询（s，t）只能使用观察（S1）来回答。由于找到一组“完美的”支持顶点在计算上很昂贵，而且我们争取线性预处理时间，我们实验评估了选择过程的不同策略。由于页面限制，我们只描述最成功的一个：向前（向后）级别i被称为中心，如果1 5Lmax≤i≤4 5Lmax，其中Lmax是最大拓扑级别。如果最多有h个顶点，其中h是O‘Reach的参数。我们首先计算一组大小最多为k·p的候选对象，它包含了向前或向后的所有顶点，一旦达到阈值k·p时，就任意丢弃顶点。P是O‘Reach的另一个参数，并与k一起控制候选集的大小。如果没有达到阈值，我们通过从所有其他正向水平为中心的顶点中均匀随机地选取缺失的顶点数来填充候选集合。下一步，得到所有候选对象的外和一致性，选择具有最大|R+(v)|·|R?(v)|的k个顶点v作为支持顶点。这种策略主要是对观察（S1）进行优化，但在实验中比另外试图优化观察（S2）和（S3）的策略效果更好。这个过程的时间复杂度为O（kp（n + m）+ kp log（kp））。
我们注意到，这是一种通用方法，已证明在不同类型的实例中工作良好，尽管可能以增加初始化时间为代价。针对不同图形类的更专门的例程可以提高运行时间和覆盖率，这似乎很自然。

4.3 The Complete Algorithm

给定一个图G和一系列查询Q，我们在下面总结了O‘Reach是如何进行的。在初始化过程中，它会执行以下步骤：
步骤1：计算wcc。
步骤2：计算前向/向后计算的拓扑级别。
步骤3：获得d个随机扩展的拓扑顺序。
步骤4：选择k个支持性的顶点，计算R+（·）和R?（·）。
步骤1和步骤2以线性时间运行。如第4.1和4.2节所示，这同样适用于步骤3和步骤4，假设所有参数都是常数。对于所有步骤，所需的空间都是线性的。可达性指数为每个顶点v包含以下信息：WCC一个整数，一个整数为F (v)和B (v)，三个整数为每个d扩展拓扑顺序τ（τ (v)，τH (v)/τL (v)，τX (v)/τN (v)），两位的k支持顶点，表明其从v的可达性。对于具有和n≤232的图，每个整数有4个字节就足够了。此外，我们将编码支持顶点和从支持顶点的位分别分组，并用一个适当大小的整数表示它们，例如，使用uint8_t（8位），对于k个≤8支持顶点。由于最小的整数在大多数架构上至少有8位，所以我们为每个顶点存储12个+ 12d + 2·k8字节。
对于每个查询查询（s、t），O‘Reach试图回答它使用下面的一个观察顺序给出，一方面已经优化了一些初步实验基准实例的小子集（详见第五节），另一方面争取公平的交替“积极”和“消极”观察，以避免过拟合。请注意，所有基于观察的测试都在恒定的时间内运行。一旦其中一个能够肯定地回答查询，结果就会立即返回。导致阳性或否定答案的测试分别标记为或。

请观察，观测（S1)-（S3）测试都可以使用布尔逻辑轻松实现，布尔逻辑允许对所有可达性信息被编码的支持进行并发测试在一个相应大小的整数中：对于观察（S1），它足以测试?（?）∧+(t)>0和r+)∧?+(t)>0和??的∧?(t)>0的观察（S2）和（S3），其中r+和r?以相同的顺序保持各自的向前和向后的可达性信息。因此，每个测试最多需要一次比较两个整数加上最多两个基本位操作。此外，请注意观测（B1）通过观测（B5）和（B6）进行隐式测试。使用上面描述的数据结构，我们的算法最多需要一个内存转移为s和一个t为每个查询（s，t）是负责的一个观察。请注意，允许识别负查询的观察结果更多，这就是为什么我们期望前者会有更明显的加速。然而，如定理4.1所述，DAGs的可达性总是小于50%，这证明了对负查询的优化的偏差。
如果查询不能使用这些测试中的任何一个来回答，我们将回到另一个算法或带有修剪的双向BFS，它对子查询（v，t）（前进步骤）或Query（s，v）（后退步骤）中每个新遇到的每个顶点使用这些测试。如果一个子查询可以通过测试决定性地回答，双向BFS可以立即地回答查询（s，t）。否则，如果一个子查询被测试回答为否定，则不再考虑遇到的顶点v（剪枝步骤）。如果子查询不能回答子查询，则顶点v将作为常规（双向）BFS添加到队列中。

5 EXPERIMENTAL EVALUATION

我们评估了我们的新算法O‘Reach作为下面列出的各种最新算法的预处理器，而不是自己运行这些算法。此外，我们使用修剪后的双向BFS（pBiBFS）作为一个额外的回退解决方案。我们的实验研究遵循[22]中的方法，包括PPL [37]、TF [3]、PReaCH [22]、IP [36]和BFL [28]算法。此外，我们的评估是第一个将IP和BFL与PReaCH直接联系起来的评估，并分别研究了IP和BFL对成功（正）和不成功（负）可达性查询的性能。出于比较的原因，我们还通过在初始化过程中完全计算输入图的传递闭包，每对顶点使用1位将其存储在一个矩阵中，并通过一个内存查找回答每个查询，来评估完全可达性矩阵的查询性能。我们将这个算法简单地称为矩阵。由于dag中的可达性很小，而且缓存局部性会影响查找时间，我们也实验了各种哈希集实现。然而，没有一种比矩阵更快或内存效率更高。

5.1 Setup and Methodology

我们在使用pBiBFS作为一个内置的回退策略的C++142中实现了O‘Reach。对于PPL、3 TF、3 PReaCH、4 IP、5和BFL6，我们在每种情况下都使用了原始的C-++实现。所有的源代码都是用GCC 7.5.0和完全优化（-O3）编译的。实验在Ubuntu 18.04下的Linux机器上运行，内核为4.15，在4个AMDOpteron6174CPU上，时钟为2.2 GHz，分别为512 kB和6 MB L2和L3缓存，每个CPU有12核。总的来说，这台机器有48核和256 GB内存。除非另有说明，每个实验都是只在一个处理器及其本地内存上按顺序运行的。由于非本地内存访问会产生一个更高的成本，这个规则的一个例外只针对矩阵，其中我们否则就只能运行12个实例，而不是29个。我们还并行化了矩阵的初始化阶段，其中计算传递闭包，使用48个线程。但是，所有的查询都是按顺序处理的。
为了抵消测量和准确性的伪影，我们在每个实例上运行每个算法5次，并且通常使用中位数进行评估。由于O‘Reach在初始化过程中使用了随机化，所以我们报告了5个不同种子的平均运行时间。对于IP和BFL，它们以相同的方式随机化，但不接受种子，我们只给出超过5次重复的平均值。我们注意到，同样取中位数或增加重复或种子的次数并不会改变整体情况。
实例。为了便于可比性，我们采用了在介绍PReaCH [22]和TF [3]的文章中使用的实例，它们与用于评估IP [36]和BFL [28]的实例重叠，这些实例可以从圣杯代码存储库7或斯坦福网络分析平台SNAP [21]获得。此外，我们通过进一步的实例大小和德拉劳内图来扩展基准图的集合。表A.4提供了一个详细的概述。由于我们只考虑dag，所有的实例都是它们各自的原始实例的浓缩，如果它们已经不是无环的话。我们还采用了[22,39]中的实例分组，并在下面只提供了不同集的简短描述。
Kronecker。这些实例是由RMAT生成器为图500基准[23]生成的，并从小到大的节点ID非循环定向。该名称将顶点的数量2i编码为kron_logni。随机：根据erdo-renyi模型（n，m）生成的图，从较小的节点到较大的节点ID。该名称编码n = 2i和m = 2j为randni-j。德劳内：来自第十届DIMACS挑战[1,8]。delaunay_ni是单位平方中2i个随机点的德劳内三角剖分。大真实：在[39]中引入，这些实例代表引文网络（citeseer.scc、密码、专利）、分类图（本体），以及蛋白质数据库RDF图（22、100、RDF图150）。小而真实密集：在[17]中引入的这些实例中，同样有引文网络（arXiv，pubmed_sub，citeseer_sub）、分类图（go_sub），以及从语义知识数据库（yago_sub）中获得的图。小的真正稀疏：这些实例是在[18]中引入的，并代表XML文档（xmark，nasa），代谢网络（mamaze，kegg）或来源于路径和基因组数据库（所有其他）。SNAP：电子邮件网络图（电子邮件-euall）、点对点网络（p2p-?31）、社交网络（soc-?1）、网络图（web-谷歌）以及通信网络（wiki-Talk）是SNAP的一部分，首次在[3]中使用。
查询。按照[22]的方法，我们分别生成了三组10万个查询：正的、负的和随机的。每个集合由随机查询组成，这些查询是通过随机选择两个顶点，分别过滤出正负查询集的负或正查询生成的。第四个查询集，是混合的，是所有正、负查询的随机打乱的联合，因此包含200,000对顶点。由于每个集合内查询的顺序由于缓存效应和内存布局对运行时间有可观察到的影响，我们随机打乱每个查询集五次，并对每次重复实验使用不同的排列，以确保所有算法的条件相同。

5.2 Experimental Results

我们从1200个候选顶点（p = 75，h = 8）中选择了k = 16个支持顶点和d = 4扩展拓扑顺序。我们使用在应用程序中也使用的两种配置运行IP作者[36]，并将得到的算法称为IP(s)（稀疏，hIP = kIP = 2）和IP(d)（密集，hIP = kIP = 5）。类似地，我们评估了BFL [28]的配置稀疏为BFL (s)（sBFL = 64）和密集为BFL (d)（sBFL = 160），遵循作者给出的预设。
平均查询时间。表A.5列出了每个查询的查询集的负集和正集的平均时间。所有缺失的值都是由于内存要求超过32 GB（TF）和Matrix（256 GB）。对于每个实例和查询集，速度最快的算法的运行时间将以粗体打印出来。如果矩阵是最快的，那么也会突出显示第二优算法的运行时间。除了矩阵，该表还显示了PReaCH、PPL、IP (d)和BFL (d)单独的运行时间，以及多个版本：一个有修剪双向BFS（O‘R +pBiBFS）作为后退，以及每个竞争对手（O’R+…），其中O‘Reach运行没有后退，未回答的查询被发送给竞争对手。类似地，表A.7给出了IP (s)、BFL (s)和TF单独的运行时间，以及作为O‘Reach的后备时间。


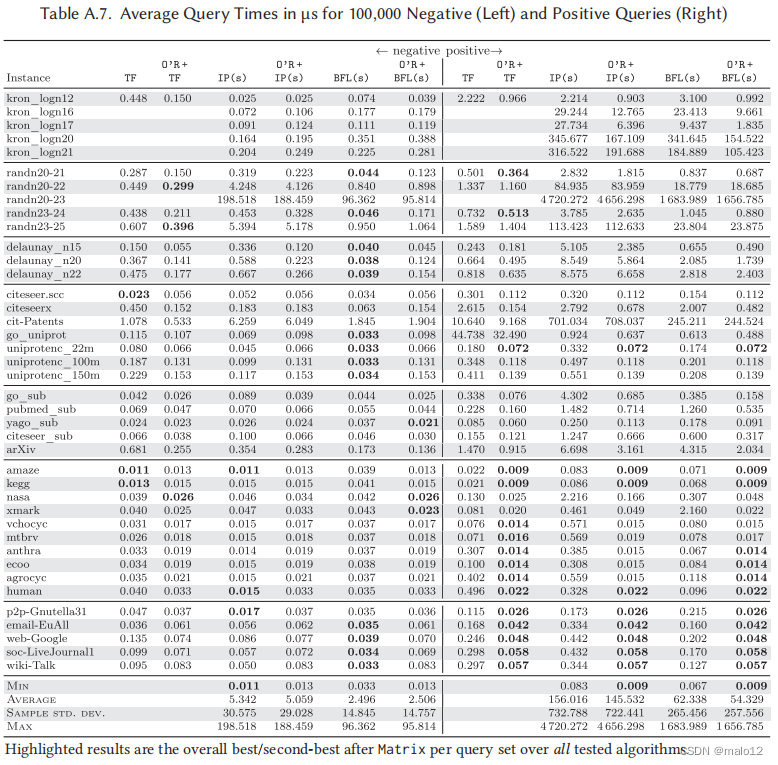
我们的结果大体上证实了由Merz和Sanders [22]进行的PReaCH、PPL和TF的性能比较。PReaCH是最快的三个五克罗内克图负面查询集，一旦击败O‘R +PReaCH和O’R+PPL，而PPL和O‘R +PPL主导所有其他积极的查询集在这个类以及三个五个随机图，而O’R +TF略快于其他两个。与[22]的研究相比，在正查询集的随机实例上，TF略优于PPL。PReaCH也是上述研究[22]中小的真实稀疏和SNAP实例的主导方法。相比之下，它在这些类上的表现是O‘Reach对正查询集的所有实例，以及对负查询集的IP (d)或BFL (s)。在Delaunay和大型真实实例中，BFL (s)通常是负查询集上最快的算法。结果还显示，BFL，特别是IP，在回答积极的查询方面存在一个弱点。在所有实例中，O‘R +PPL对负查询和正查询的平均查询时间最快。
值得注意的是，矩阵经常表现出色，特别是对于集合为负的查询，这与这些查询的很大一部分可以通过恒定时间观察来回答（参见下面对观察有效性的详细分析）相关，这是由于其更大的内存占用。在所有的实例和种子中，这个集合中超过95 %的查询可以通过O‘Reach直接回答。集积极，矩阵的平均查询时间在几乎所有情况下都小于负查询集，这可以解释为实例的小可达性和结果更高的空间定位和更好的可缓存性和自然集群矩阵中的一个条目。因此，对于混合查询集，这种效果明显降低了，如表A.6所示。

在某些情况下，O‘Reach对正查询集的回复率超过90 %，例如，在cit专利上，这清楚地反映在运行时间上。除了PPL外，所有的算法在这个实例上都有处理阳性查询的困难。相反，所有uniprotenc_?实例和citeseer.scc的后退率均为0%。在所有的实例和种子中，O‘Reach平均可以通过恒定时间的观察回答超过70 %的积极查询。
关于随机和混合的查询集的结果是相似的，并在表中列出A.6和A.8.同样，O‘R +PPL在两个查询集的所有实例中都显示出了平均最快的查询时间。由于DAG中的可达性一般较低（参见定理4.1），特别是在基准测试实例中，随机的平均查询时间与负的相似。另一方面，混合查询集的结果与正查询集的结果更相似，因为算法之间性能的相对差异更明显。表2紧凑地显示了每个查询集的所有实例上的平均查询时间。只有PPL和O‘R +PPL实现的平均查询时间小于1μs（甚至小于0.35μs）。

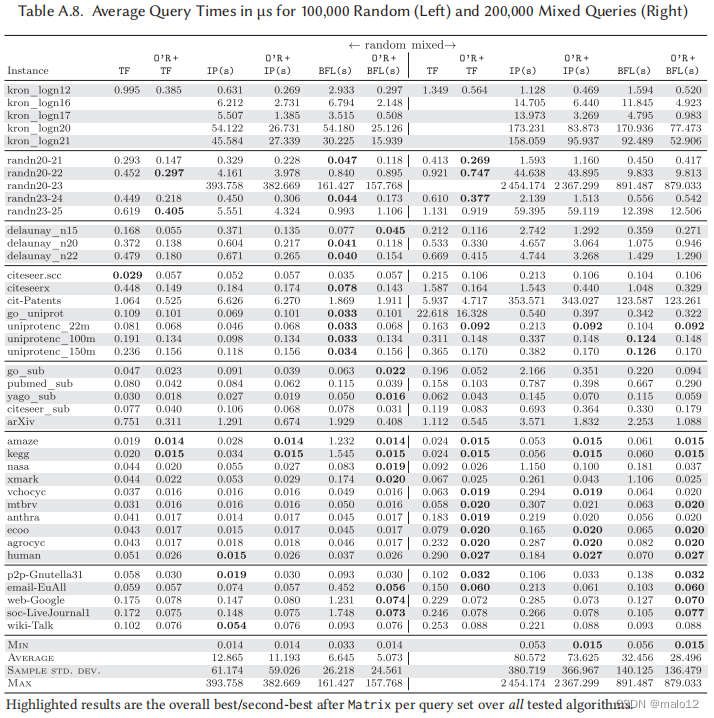
O‘Reach加速。接下来，我们研究了不同的后备解决方案对O‘Reach的相对加速。表A.9列出了所有四个查询集的每个竞争对手算法单独运行的平均查询时间除以O‘Reach的平均查询时间加上该算法作为回调的比率。在表3中还给出了一个紧凑的版本。在大多数情况下，使用O‘Reach作为预处理器导致加速，除了负面或随机查询BFL和部分IP大型实际实例以及PReaCH和部分IP小实际稀疏和SNAP实例。在kegg上的BFL的随机查询可以实现最大的约105个的加速。对于正查询集、随机查询算法和混合查询集上的所有后退算法，平均加速（几何）至少为1.29，其中正查询上的IP (s)达到最大值，系数为4.21。

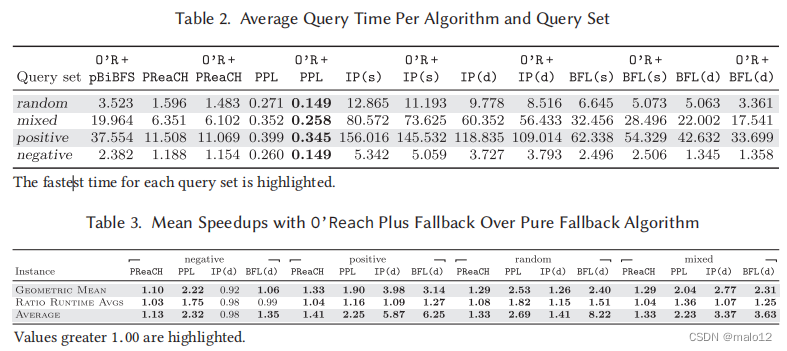
只有对于纯粹的负查询，IP (d)和BFL (s)单独在平均值上要快一些。图A.2给出了对值分布的更多了解，并显示了与O‘Reach的组合导致了在正查询集和混合查询集上的大多数实例上的所有算法以及随机算法都有不同的加速。对于负查询集，与O‘Reach的组合可以特别加快所有实例上PPL的平均查询时间，对于超过75 %的实例上的TF，对于PReaCH和BFL (d)仍然在大约一半的实例上的平均查询时间。总之，考虑到这些算法通常已经比单个内存查找更快，通过O‘Reach实现的加速相当高。
初始化时间（表A.10)。在所有的图中，BFL (s)的初始化时间最快，其次是BFL (d)和PReaCH。达到，计算的开销比较大的适应的1200候选人k = 16支持顶点清楚地反映在运行时间密集的实例和可以大大减少如果选择低参数，尽管略微降低查询性能，例如，k=8。PPL经常在这一步骤中消耗大量的时间，特别是在更密集的情况下，在randn20-23上最多需要2.6小时。

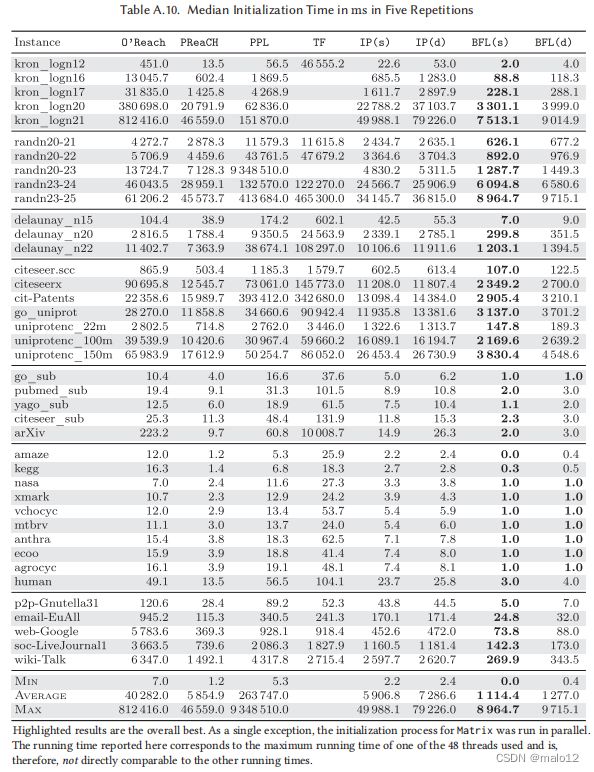
基于每个实例的平均查询时间，如果O‘Reach作为预处理器运行，则摊销初始化时间额外投资所需的最小随机查询数在96000（O’R+BFL(d)）到499000（O‘R+PReaCH）之间。计算O‘Reach不能在平均查询时间内实现加速的情况，摊销所需的随机查询的中位数在250万（O’R +BFL (d)）到1.01亿（O‘R +IP (d)）之间。对于平均最快的算法O‘R +PPL，在21万（nasa）到61.5亿（kron_logn21）随机查询后恢复初始化成本，分别相当于所有顶点对的0.77 %（nasa）和0.14 %（kron_logn21）。
观察的有效性。我们收集了大量的统计数据，对O‘Reach中使用的不同观察结果的有效性进行分析。为了使分析更加可靠，我们添加了额外的种子，并将种子数量增加到25个。对于每个观察，我们维护一个单独的计数器，当观察可以回答查询时，这个计数器就会增加。如果观察包括多个测试，如基于拓扑顺序(（B4）、（T1）-（T6））或支持顶点（（S1）-（S3））的测试，每次观察只增加一次，即使例如（B4）应用两个拓扑顺序或（S1）应用多个支持顶点。然后，我们获得了每个观察结果的平均有效性，即计数器值与我们想要考虑的查询数量的平均比值，并接管了所有的种子和所有实例。8结果也如表A.12所示。

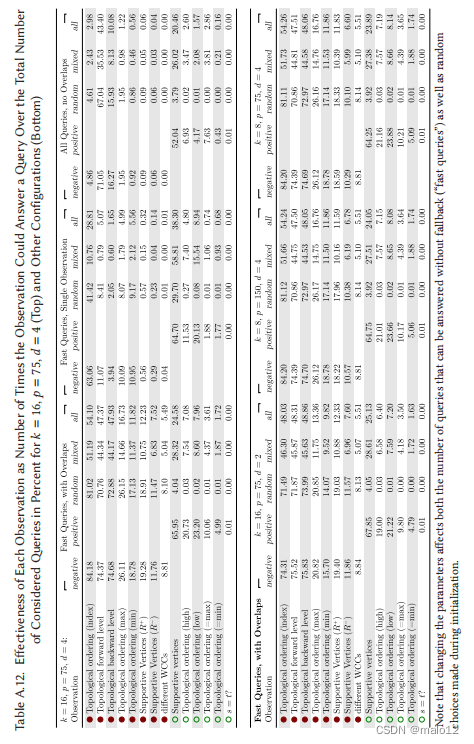
首先，我们只查看快速查询，即那些可以回答而无需回调的查询。我们增加了所有可以回答此分析查询的观察结果的计数器，而不仅仅是第一个顺序，这就是为什么可能存在重叠（一个查询可以回答多次）。在所有查询集中，最有效的观察是对拓扑顺序的负基本观察（B4），它可以回答所有快速查询的54 %。由于随机查询集中的平均可达性非常低，因此负查询在总体情况中占主导地位。因此，最有效的观察结果是否定的，这也就不足为奇了。在负查询集上，它甚至可以回答84 %的快速查询。在有效性方面，仅次于（B4）的负面观察是那些关注正向和向后拓扑水平，观察（B5）和（B6），它们在负查询集上分别可以回答约74.5 %，约所有快速查询的47.5 %。使用扩展拓扑排序的max和min索引（T2）和（T5）的观察，可以回答负查询集中26 %和19 %的快速查询，以及基于支持顶点的观察，（S2）和（S3）的观察，分别为19 %和12 %。
将拓扑排序数量从d = 4降低到d = 2后，（B4）与（B5）和（B6）同样有效，每个都可以回答大约48 %的快速查询和75 %的负查询。观察到，减少d会对快速查询的数量产生负面影响，进而导致（B5）和（B6）的比率略有增加。对于观察结果（T2）和（T5），在负查询集上的有效性降低到21 %和16 %，在所有查询集上的有效性降低到13 %和10 %。
在所有查询集中，最有效的积极观察和第二好的是基于支持顶点的观察（S1），它可以回答所有快速查询中约25 %的问题，而正查询集中的66 %。后续观察结果分别使用了高指数和低指数（T1）和（T4），对正查询集的有效性分别为21 %和23 %，对所有查询集的有效性约为7.5 %。剩下的两个组，（T3）和（T6），在阳性组中可以分别回答10 %和5%。
减少支持顶点的数量从k=16k=8导致小减少观察的有效性（S1）约64.5 %的积极查询，如果候选人的数量保持平等（p = 150）或减少类似（p = 75）。将拓扑排序数减少到d = 2会导致（T1）和（T4）的轻微恶化，达到19 %和21 %，以及相对于正查询集的5%。
在所有快速查询只能回答一个观察，最有效的观察是积极的支持基于顶点的观察（S1）有38 %的所有查询集和65 %的积极的查询集，紧随其后的是消极的基本观察使用拓扑顺序，（B4），约29 %的所有查询集和63 %的负面查询集。
现在查看整个查询集，我们的统计数据显示，95 %的查询可以通过对负查询集的观察来回答。在70 %的情况下，（B5）在第二次测试中使用拓扑的正向级别，已经可以回答查询。在另外16 %的例子中基于拓扑反向水平的观察（B6）是成功的。在正查询集上，回调率约为29 %，因此高于负查询集。该集合中52 %的查询可以通过基于支持顶点的观察（S1）来回答，扩展拓扑排序（T1）和（T4）的高和低指数分别占7%和4%。请注意，在这里，可以回答查询的顺序中的第一个观察结果“wins the point”，也就是说，这里的有效性取决于顺序，并且在报告的有效性中没有重叠。
内存消耗。表A.11列出了每种算法用于其可达性索引的内存。由于O‘Reach配置了k = 16和d = 4，其索引大小为64n字节。因此，O‘Reach、PReaCH、PPL、IP的可达性指数和BFL，除了一个例外，对于所有小的真实实例都适合6 MB的L3缓存。矩阵，这只是四个最小的实例从小的稀疏集，三个小的真正密集的，和最小的克罗内克图，这清楚地反映在其平均查询时间的负面，随机，在较小的程度上，混合查询集。而对于O‘Reach、PReaCH和矩阵，索引的大小仅仅取决于顶点的数量，IP、BFL、PPL和TF的内存消耗的密度越大。IP (s)通常是最有效的，使用从不超过395 MB，其次是BFL (s)（429 MB）、IP (d)（440 MB）、BFL (d)（754 MB）、PReaCH（1.3 GB）、O‘Reach（1.5 GB）和PPL（4.4 GB）。因此，所有这些算法都适用于处理具有数百万个顶点的图，即使是在内存相对较少的硬件上（相对于当前的标准而言）。TF最多使用了3.8 GB（randn23-25），但在表中缺少数据的所有实例中，在初始化期间至少需要超过64 GB。

6 CONCLUSION

在本文中，我们重新讨论了针对静态可达性问题的现有技术，并将它们与新的方法结合起来，使用线性大小的可达性指数在恒定时间内支持大部分可达性查询。我们广泛的实验评估表明，在几乎所有的场景中，将任何现有的算法与我们在O‘Reach中实现的新技术相结合，都可以通过几个因素加快查询时间。特别是，支持性的顶点已经被证明对快速回答正的查询是有效的。此外，O‘Reach是灵活的：内存使用、初始化时间和预期查询时间可以直接受到三个参数的影响，这些参数允许用空间交换时间，用初始化时间交换查询时间。此外，我们的研究表明，由于缓存效应，在空间上的高投资不一定会有回报：在预先计算的全可达性矩阵中，可达性查询通常比单个内存访问回答得快得多。
在所有实例和查询类型中，平均最快的算法是O‘Reach和PPL的组合，平均查询时间小于0.35μs。由于PPL的初始化时间相对较高，我们还建议O‘Reach与PReaCH结合作为初始化时间和部分内存的低成本替代方案，在所有查询集上的平均查询时间最多为11.1μs。