近似点梯度法
最优化笔记——Proximal Gradient Method
最优化笔记，主要参考资料为《最优化：建模、算法与理论》
文章目录
一、邻近算子
（1）定义
定义 (邻近算子)
对于一个凸函数 h h h, 定义它的邻近算子(proximal operator)为
prox ? h ( x ) = arg ? min ? u ∈ d o m h { h ( u ) + 1 2 ∥ u ? x ∥ 2 } . \operatorname{prox}_h(x)=\arg\min_{u\in\mathbf{dom}h}\left\{h(u)+\frac12\|u-x\|^2\right\}. proxh?(x)=argu∈domhmin?{h(u)+21?∥u?x∥2}.
可以看到，邻近算子的目的是求解一个距 x x x 不算太远的点，并使函数值 h ( x ) h(x) h(x) 也相对较小.
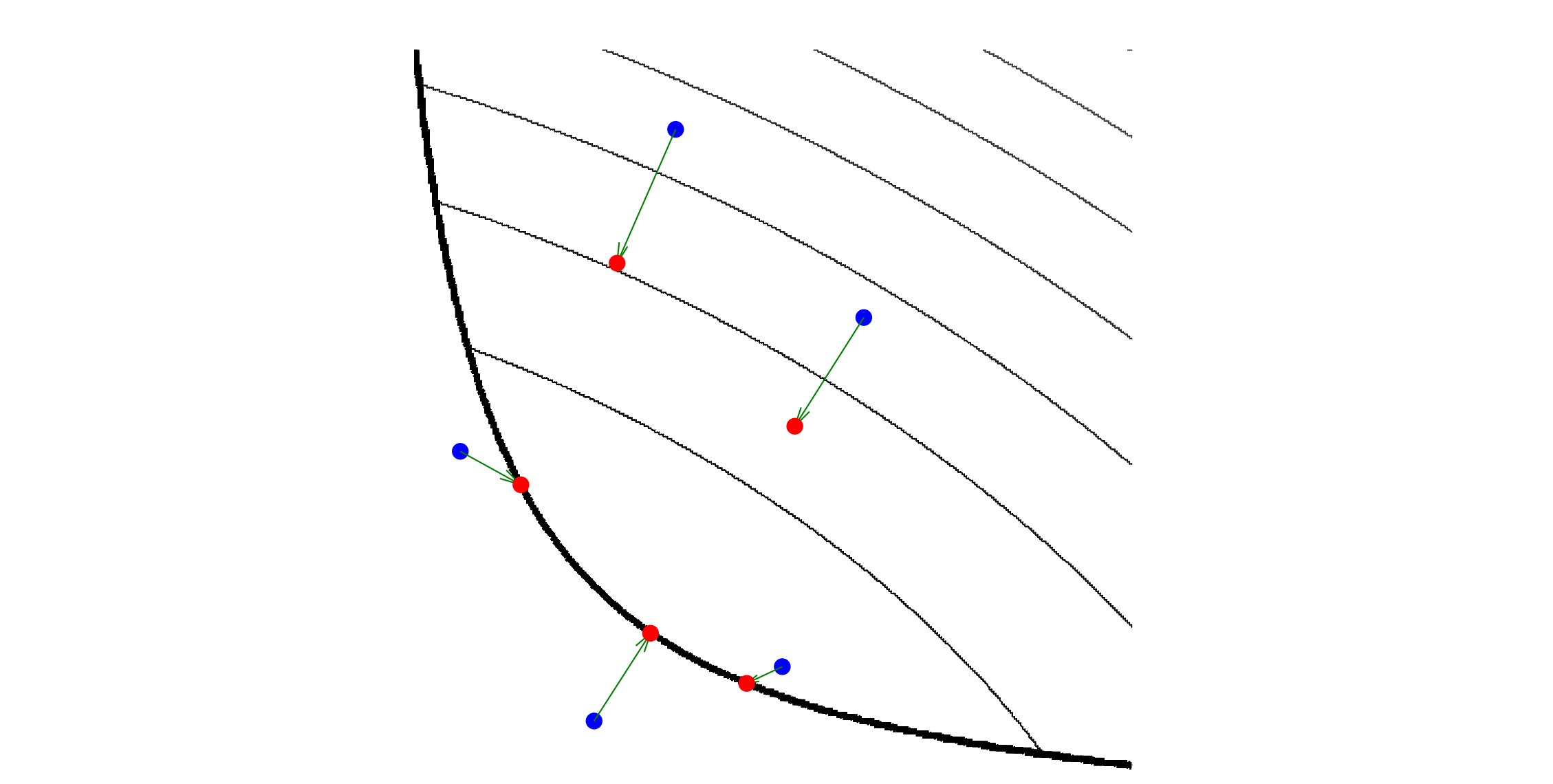
上图图描述了proximal算子的作用:
- 细黑线是凸函数 h ( x ) h(x) h(x)的等高线;较粗的黑线表示定义域的边界.
- 设蓝点为 x x x，计算 μ = prox ? h ( x ) \mu=\operatorname{prox}_h(x) μ=proxh?(x)，红点则是 μ \mu μ.
- 定义域内的三个点其对应的 μ \mu μ停留在定义域内，并向 h ( x ) h(x) h(x)最小值移动.
- 而另外两个定义域外的点，其对应的 μ \mu μ移动到定义域的边界，并尽可能使 h ( u ) h(u) h(u)很小.
一个很自然的问题是，上面给出的邻近算子的定义是不是有意义的，即定义中的优化问题的解是不是存在唯一的. 若答案是肯定的，我们就可使用邻近算子去构建迭代格式. 下面的定理将给出定义中优化问题解的存在唯一性.
定理 (邻近算子是良定义的)
如果 h h h 是适当的闭凸函数，则对任意的 x ∈ R n , p r o x h ( x ) x\in\mathbb{R}^n,\quad\mathrm{prox}_h(x) x∈Rn,proxh?(x) 的值存在且唯一.
二、近似点梯度法
（1）迭代格式
考虑如下复合优化问题：
min ? ψ ( x ) = f ( x ) + h ( x ) , \min\quad\psi(x)=f(x)+h(x), minψ(x)=f(x)+h(x),
其中函数 f f f 为可微函数，其定义域 d o m f = R n \mathbf{dom}f=\mathbb{R}^n domf=Rn, 函数 h h h 为凸函数，可以是非光滑的，并且一般计算此项的邻近算子并不复杂. 比如 LASSO 问题，两项分别为 f ( x ) = 1 2 ∥ A x ? b ∥ 2 , h ( x ) = μ ∥ x ∥ 1 . f(x)=\frac12\|Ax-b\|^2,\quad h(x)=\mu\|x\|_1. f(x)=21?∥Ax?b∥2,h(x)=μ∥x∥1?. 近似点梯度法的思想非常简单：注意到 ψ ( x ) \psi(x) ψ(x) 有两部分，对于光滑部分 f f f 做梯度下降，对于非光滑部分 h h h 使用邻近算子，则近似点梯度法的迭代公式为
x k + 1 = p r o x t k h ( x k ? t k ? f ( x k ) ) , ( 1 ) x^{k+1}=\mathrm{prox}_{t_kh}(x^k-t_k\nabla f(x^k)), \quad (1) xk+1=proxtk?h?(xk?tk??f(xk)),(1)
其中 t k > 0 t_k>0 tk?>0 为每次迭代的步长，它可以是一个常数或者由线搜索得出. 近似点梯度法跟众多算法都有很强的联系，在一些特定条件下，近似点梯度法还可以转化为其他算法：当 h ( x ) = 0 h(x)=0 h(x)=0 时，迭代公式变为梯度下降法
x k + 1 = x k ? t k ? f ( x k ) ; x^{k+1}=x^k-t_k\nabla f(x^k); xk+1=xk?tk??f(xk);
当 h ( x ) = I C ( x ) h(x)=I_C(x) h(x)=IC?(x) 时，迭代公式变为投影梯度法
x k + 1 = P C ( x k ? t k ? f ( x k ) ) . x^{k+1}=\mathcal{P}_C(x^k-t_k\nabla f(x^k)). xk+1=PC?(xk?tk??f(xk)).
（2）迭代格式的理解
对
f
(
x
)
f(x)
f(x)在
x
k
x^k
xk处做泰勒展线性展开并加上二次项，非光滑部分不做改变：
min
?
x
f
(
x
)
+
h
(
x
)
??
?
??
min
?
x
f
(
x
k
)
+
?
f
(
x
k
)
T
(
x
?
x
k
)
+
1
2
t
k
∥
x
?
x
k
∥
2
+
h
(
x
)
(
2
)
??
?
??
min
?
x
1
2
t
k
∥
x
?
x
k
+
t
k
?
f
(
x
k
)
∥
2
+
h
(
x
)
(
3
)
??
?
??
min
?
x
1
2
t
k
∥
x
?
(
x
k
?
t
k
?
f
(
x
k
)
)
∥
2
+
h
(
x
)
(
4
)
\begin{aligned} &\min_x f(x)+h(x) \\ \iff &\min_x f(x^k)+\nabla f(x^k)^\mathrm{T}(x-x^k)+\frac1{2t_k}\|x-x^k\|^2+h(x) \quad(2) \\ \iff &\min_x \frac1{2t_k}\|x-x^k+t_k\nabla f(x^k)\|^2+h(x)\quad (3) \\ \iff &\min_x \frac1{2t_k}\|x-(x^k-t_k\nabla f(x^k))\|^2+h(x) \quad(4) \end{aligned}
????xmin?f(x)+h(x)xmin?f(xk)+?f(xk)T(x?xk)+2tk?1?∥x?xk∥2+h(x)(2)xmin?2tk?1?∥x?xk+tk??f(xk)∥2+h(x)(3)xmin?2tk?1?∥x?(xk?tk??f(xk))∥2+h(x)(4)?
可以看到(4)式即为邻近算子的定义
x
k
+
1
=
prox
?
t
k
h
(
x
k
?
t
k
?
f
(
x
k
)
)
x^{k+1}=\operatorname{prox}_{t_{k}h}(x^k-t_k\nabla f(x^k))
xk+1=proxtk?h?(xk?tk??f(xk))
相当于是对
f
(
x
)
f(x)
f(x)先做一步梯度下降
x
^
k
+
1
=
x
k
?
t
k
?
f
(
x
k
)
\hat{x}^{k+1}=x^k-t_k\nabla f(x^k)
x^k+1=xk?tk??f(xk)，然后再寻找一个点
x
k
+
1
x^{k+1}
xk+1，使得
x
k
+
1
x^{k+1}
xk+1距
x
^
k
+
1
\hat{x}^{k+1}
x^k+1 不算太远，并使函数值
h
(
x
^
k
+
1
)
h(\hat{x}^{k+1})
h(x^k+1) 也相对较小.
（3）收敛性分析
也就是说近似点梯度法收敛速度是 O ( 1 k ) O(\frac1k) O(k1?)的，比次梯度算法快！
三、FISTA算法
（1）迭代格式
注意每个Section公式重新从（1）开始编号
仍然考虑复合优化问题
min
?
ψ
(
x
)
=
f
(
x
)
+
h
(
x
)
.
(
1
)
\min\quad\psi(x)=f(x)+h(x)\quad. (1)
minψ(x)=f(x)+h(x).(1)
上面介绍的近似点梯度法收敛速度是
O
(
1
k
)
O(\frac1k)
O(k1?)的，下面介绍一个在此基础上改进的算法——FISTA，收敛速度可以达到
O
(
1
k
2
)
O(\frac1k^2)
O(k1?2)!
（2）收敛性分析
参考资料
- 刘浩洋、户将、李勇锋、文再文. 最优化：建模、算法与理论. 高教出版社, 2022.
- http://faculty.bicmr.pku.edu.cn/~wenzw/
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！