欠采样对二维相位展开的影响
1.前言
如前所述,相位展开器通过计算两个连续样本之间的差来检测图像中包裹的存在。如果这个差值大于+π或小于-π,则相位展开器认为在这个位置存在包裹。这可能是真正的相位包络,也可能是由噪声或采样不足引起的伪包络。
对欠采样的相位图像进行相位展开可能很困难,或者在某些情况下甚至不可能。当两个连续样本之间的差异大于+π或小于-π时,就会发生这种情况。相邻样本之间的这种大差异仅仅是由于相位图像不包含足够的样本这一事实而存在的,而不是由于真实相位包络的存在。这种情况会自动生成不正确的“假包装”。
让我们首先回顾欠采样对1D相位展开过程的影响。根据奈奎斯特采样理论(Nyquist?
sampling theory),如果函数f(x)不包含高于B Hertz的频率,则可以通过以2B或更大的速率对其进行采样来完全确定。在以下情况下f(x)是一个纯正弦信号,那么中的每个周期f(x)必须至少用两个样本进行采样。这一原理也适用于包裹的相位信号。
假设我们考虑如图7(a)所示的1D连续相位信号。该信号包含20个样本,并且正好覆盖循环波形的一个周期。该信号被相位包裹,如图7(b)所示。这个被包裹的信号以足够高的速率被采样,并且它包含四个真正的包裹。该包裹信号可以使用1D Itoh算法进行相位展开,展开结果如图7(c)所示。注意,在这种情况下,相对简单的1D Itoh算法正确地展开了包裹的相位信号。这里还需要注意的是,虽然展开信号的形状与原始信号相同,但图上每个点的实际相位值现在不同,即图7(a)中的原始信号的范围为+6到-6弧度,而图7(c)中的展开信号的范围从0到-12弧度。您应该知道,大多数相位展开器只产生这样的“相对”相位值,而不是“绝对”相位值作为其输出.一些高级展开器每次执行代码时都会产生相同形状的相对相位输出,但绝对相位值的数字不同。您应该意识到,可以采用某些测量策略,实际测量绝对相位,而不是相对相位。

图7:(a)包含20个样本的连续相位信号。(b) 相位包裹的信号。(c) 相位展开信号。?
现在,让我们减少图7(a)中出现的同一1D相位信号中的样本数量,将采样率减半,使该信号现在只采集10个样本,如图8(a)所示。该信号随后被封装,如下图8(b)所示。这个包裹的信号现在包含四个真包裹和两个假包裹。这两个假包裹是由于信号采样不足而发生的,它们的位置如图8(b)所示。第三个和第四个样本之间的差异小于-π。相位展开器会将这个大的差异视为一个包裹,并将向第四个样本以及其右侧的所有样本添加2π的值,如图8(c)所示。这将破坏整个一维相位解包信号。同样,第八个和第九个采样点之间的差值大于 +π,相位解包器会再次将其视为包络,因此会从第九个和第十个采样点中减去 2π 的值,如图 8(c)所示。这也会破坏一维相位解包信号的其余部分。请注意,相位 与图 8(a)中所示的原始连续相位信号完全不同。图 8(a)中所示的原始连续相位信号完全不同。请注意,这里的信号是使用一维itoh算法处理的。
 图8:(a)现在只包含10个样本的连续相位信号。(b) 包裹的信号。(c) 展开的信号
图8:(a)现在只包含10个样本的连续相位信号。(b) 包裹的信号。(c) 展开的信号
接下来,我们将使用计算机生成的欠采样相位图像来解释欠采样对2D相位展开算法的影响。首先,我们将创建人工欠采样相位图像。然后,我们将根据采样理论,从理论上分析计算机生成的相位图像,以研究特定数据集在x和y方向上的最大允许采样率。接下来我们将包装这些图像。之后,我们将使用两种不同的相位展开算法来处理这些图像:即Itoh算法和2D-SRNCP算法。最后,我们将把这两个展开器产生的图像与原始的连续相位图进行比较。
2.理论分析
假设我们有计算机生成的连续相位图像f(x,y),其在图9(a)和(b)中显示为视觉强度阵列和3D表面,并由方程表示;
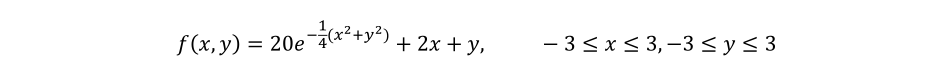
?现在我们将根据采样理论来分析该模拟相位图像。您之前应该已经完成了1D相位展开教程,您可能希望查看该文档中关于欠采样的1D讨论,这将有助于您理解下面关于2D中欠采样的讨论。
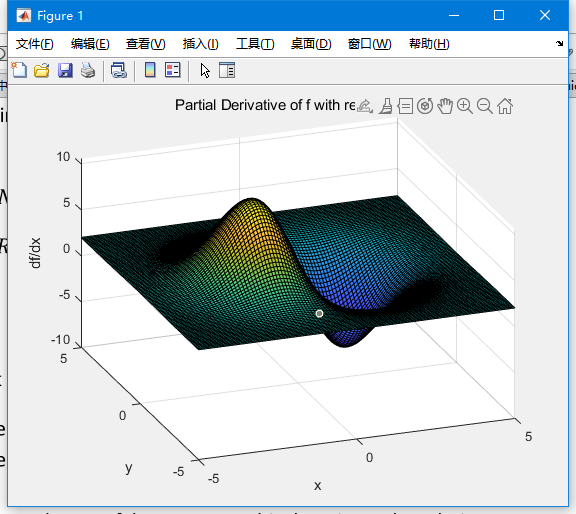
首先,让我们找到该数据集在x方向上的最大相位变化率。相位图像在x方向上的相位变化率如图9(c)所示,这是由以下方程给出的,该方程是由上述方程关于x的偏微分产生的
?
% 定义 x 和 y 的范围
x = linspace(-5, 5, 100);
y = linspace(-5, 5, 100);
% 为 x 和 y 创建一个网格
[X, Y] = meshgrid(x, y);
% 计算偏导数的值
Z = -10 .* X .* exp(-1/4 .* (X.^2 + Y.^2)) + 2;
% 绘制三维曲面图
surf(X, Y, Z)
title('Partial Derivative of f with respect to x')
xlabel('x')
ylabel('y')
zlabel('df/dx')
x方向上最大相位变化的位置实际上发生在该连续相位图像中的x=-1.4172和y=-0.0015的点处(图片中的两个极值点处,通过对其导函数再求导)。该位置的最大相位变化值为10.5776弧度。
因此,如果x方向上的连续样本必须改变小于pi的值,以便它们不会被错误地标记为包裹,那么采样率(一个周期中的样本数量,表示为Nx)将由给出;
?
?此示例中在x方向上采样的实际数据点的数量Nrx由以下方程给出

其中Nx是x方向上的采样率Rx是x轴的数据范围,对于这里给出的示例,是范围Rx?=6(6=3-3)?然后,根据上述方程;

?因此,在此生成的连续相位图像必须在x方向上用至少21个样本进行采样,否则将被欠采样。如果在x方向上以小于21个样本对其进行采样,则这种欠采样可能导致两个连续样本之间的差大于pi,这将在由展开算法处理时在该位置错误地产生假包裹。
类似地,相位图像在y方向上的相位变化率如图9(d)所示,并由以下方程给出,该方程由以下方程的偏微分产生:f(x,y)在本节开始时呈现,这次是关于y;

% 定义 x 和 y 的范围
x = linspace(-5, 5, 100);
y = linspace(-5, 5, 100);
% 为 x 和 y 创建一个网格
[X, Y] = meshgrid(x, y);
% 计算偏导数的值
Z = -10 .* Y .* exp(-1/4 .* (X.^2 + Y.^2)) + 2;
% 绘制三维曲面图
surf(X, Y, Z)
title('Partial Derivative of f with respect to x')
xlabel('x')
ylabel('y')
zlabel('df/dx')
y方向上的最大相位变化的位置出现在该连续相位图像中的x=-0.0044和y=-1.4143的点处。在这个位置,y的最大相位变化值为9.5776 radians
因此,如果y方向上的连续样本必须改变小于pi的值,以便它们不会被错误地标记为包裹,则采样率(一个周期中的样本数量,表示为Ny)将由给出

此示例中在y方向上采样的实际数据点的数量Nry由以下方程给出;

?其中,Ny是y方向上的采样率Ry是y轴的数据范围,对于这里给出的示例,是范围R_y?=6(6=3-3)。
然后,根据上述方程;

因此,这里已经生成的连续相位图像必须在y方向上用至少19个样本进行采样,以避免采样不足和错误地产生假包裹。
下面给出了创建和绘制该模拟连续相位数据集的代码,以及相位的x和y变化率;
% % 定义 x 和 y 的范围
% x = linspace(-5, 5, 100);
% y = linspace(-5, 5, 100);
%
% % 为 x 和 y 创建一个网格
% [X, Y] = meshgrid(x, y);
%
% % 计算偏导数的值
% Z = -10 .* Y .* exp(-1/4 .* (X.^2 + Y.^2)) + 2;
%
% % 绘制三维曲面图
% surf(X, Y, Z)
% title('Partial Derivative of f with respect to x')
% xlabel('x')
% ylabel('y')
% zlabel('df/dx')
clc; close all; clear
NRx = 512; NRy=512;
tx = linspace(-3,3,NRx);
ty = linspace(-3,3,NRy);
[x,y]=meshgrid(tx,ty);
image1 = 20*exp(-0.25*(x.^2 + y.^2)) + 2*x + y;
figure, colormap(gray(256)), imagesc(tx,ty,image1)
title('Original image displayed as a visual intensity array')
xlabel('x axis'), ylabel('y axis')
figure
surf(x,y,image1,'FaceColor','interp', 'EdgeColor','none', 'FaceLighting','phong')
view(-30,30), camlight left, axis tight
title('Original image displayed as a surface plot')
xlabel('x axis'), ylabel('y axis'), zlabel('Phase in radians')
xdiff = diff(image1')';
figure, colormap(gray(256)), imagesc(tx(1:end-1),ty,xdiff)
title('Phase change in the x direction')
xlabel('x axis'), ylabel('y axis')
ydiff = diff(image1);
figure, colormap(gray(256)), imagesc(tx,ty(1:end-1),ydiff)
title('Phase change in the y direction')
xlabel('x axis'), ylabel('y axis') ?
图9:(a)和(b)计算机生成的连续相位图像。(c) &(d)计算机生成的相位图像分别在x和y方向上的相位变化。这里,NRx=512,NRy=512。继续。。。?
计算机生成的连续相位图像现在可以被人工包裹,其结果如图9(e)和(f)所示。使用Itoh算法展开包裹的相位图像:使用第一种方法实现,如图9(g)和(h)所示。接下来,使用Itoh算法对包裹的相位图像进行展开:使用第二种方法实现,结果如图9(i)和(j)所示。最后,使用2D-SRNCP算法对包裹的相位图像进行展开,如图9(k)和(l)所示。?
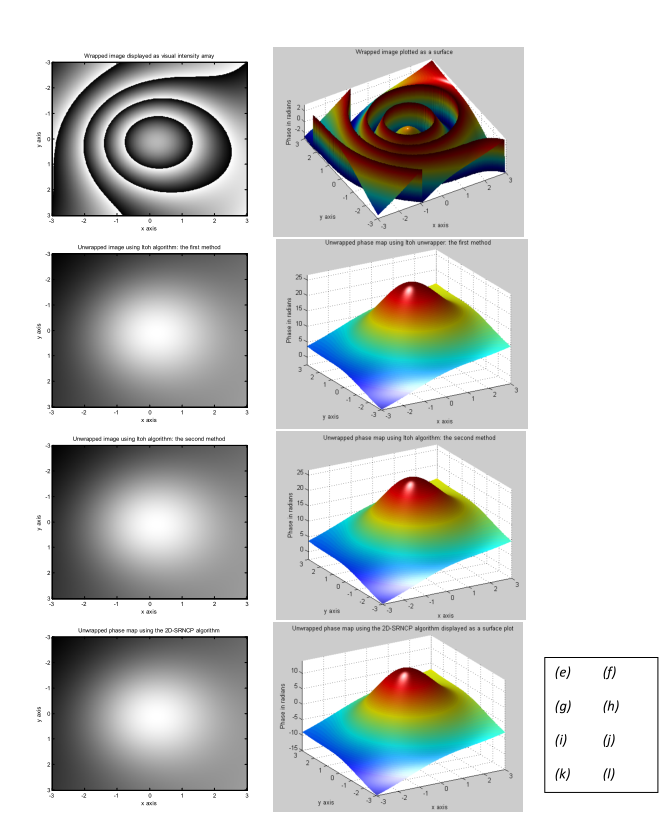
图9:续。(e) &(f)包装图像。使用(g)和(h)Itoh算法的图像展开器:第一种方法,(i)和(j)Itoh方法:第二种方法,以及(k)和(l)2D-SRNCP算法。这里,采样率很高,NRx=512,NRy=512?
用于生成图9所示所有图像的Matlab代码如下所示。这里,NRx的值被设置为512,而NRy的相应值被设置成512。请注意,所有三种相位展开算法都成功地正确展开了包裹的相位图像,如图9(e)所示。
%wrap the 2D image
image1_wrapped = atan2(sin(image1), cos(image1));
figure, colormap(gray(256)), imagesc(tx,ty,image1_wrapped)
title('Wrapped image displayed as a visual intensity array')
xlabel('x axis'), ylabel('y axis')
figure
surf(x,y,image1_wrapped,'FaceColor','interp', 'EdgeColor','none',
'FaceLighting','phong')
view(-30,70), camlight left, axis tight
title('Wrapped image plotted as a surface')
xlabel('x axis'), ylabel('y axis'), zlabel('Phase in radians')
%Unwrap the image using the Itoh algorithm: implemented using the first method
%Unwrap the image by firstly unwrapping all the rows, one at a time.
image1_unwrapped = image1_wrapped;
for i=1:NRy
image1_unwrapped(i,:) = unwrap(image1_unwrapped(i,:));
end
%Then unwrap all the columns, one at a time
for i=1:NRx
image1_unwrapped(:,i) = unwrap(image1_unwrapped(:,i));
end
figure, colormap(gray(256)), imagesc(tx,ty,image1_unwrapped)
title('Unwrapped image using the Itoh algorithm: the first method')
xlabel('x axis'), ylabel('y axis')
figure
surf(x,y,image1_unwrapped,'FaceColor','interp', 'EdgeColor','none',
'FaceLighting','phong')
view(-30,30), camlight left, axis tight
title('Unwrapped phase map using the Itoh unwrapper: the first method')
xlabel('x axis'), ylabel('y axis'), zlabel('Phase in radians')
%Unwrap the image using the Itoh algorithm: implemented using the second method
%Unwrap the image by firstly unwrapping all the columns one at a time.
image2_unwrapped = image1_wrapped;
for i=1:NRx
image2_unwrapped(:,i) = unwrap(image2_unwrapped(:,i));
end
%Then unwrap all the a rows one at a time
for i=1:NRy
image2_unwrapped(i,:) = unwrap(image2_unwrapped(i,:));
end
figure, colormap(gray(256)), imagesc(tx,ty,image2_unwrapped)
title('Unwrapped image using the Itoh algorithm: the second method')
xlabel('x axis'), ylabel('y axis')
figure
surf(x,y,image2_unwrapped,'FaceColor','interp', 'EdgeColor','none',
'FaceLighting','phong')
view(-30,30), camlight left, axis tight
title('Unwrapped phase map using the Itoh algorithm: the second method')
xlabel('x axis'), ylabel('y axis'), zlabel('Phase in radians')
%call the 2D phase unwrapper from the C language
%To compile the C code: in Matlab Command Window type
% mex Miguel_2D_unwrapper.cpp
%The wrapped phase should have the single data type (float in C)
WrappedPhase = single(image1_wrapped);
UnwrappedPhase = Miguel_2D_unwrapper(WrappedPhase);
figure, colormap(gray(256))
imagesc(tx,ty,UnwrappedPhase);
xlabel('x axis'), ylabel('y axis')
title('Unwrapped phase map using the 2D-SRNCP algorithm')
figure
surf(x,y,double(UnwrappedPhase),'FaceColor','interp', 'EdgeColor','none',
'FaceLighting','phong')
view(-30,30), camlight left, axis tight
title('Unwrapped phase map using the 2D-SRNCP displayed as a surface plot')
xlabel('x axis'), ylabel('y axis'), zlabel('Phase in radians')现在重复上述过程,但这次降低了采样率,将NRx设置为值23,将NRy设置为值21。从结果中注意到,所有的相位展开算法都成功地展开了如图10(c)所示的包裹相位图像。得到的展开相位图像如图10所示。

?图10:(a)和(b)计算机生成的连续相位图像。(c) &(d)包装图像。使用(e)和(f)Itoh算法展开图像:第一种方法,(g)和(h)Itoh方法:第二种方法。继续。。。

图10:续(i)和(j)2D-SRNCP算法。这里,采样率已经降低,但仍高于理论最小允许极限,NRx=23,NRy=21
?现在再次重复上述过程,但这一次NRx设置为值20,NRy设置为值18(即低于理论最小采样率)。通过将NRx和NRy设置为这些值,现在对计算机生成的连续相位图像进行欠采样。从结果中可以看出,如图11(e)-(h)所示,Itoh算法未能正确打开包裹的相位图像。这里,由欠采样引起的假包裹产生的误差在整个图像中传播。另一方面,2D-SRNCP相位展开器虽然不能防止误差的发生,并且它们明显存在于展开的相位图中,但它确实防止了这些误差在图像中传播并破坏良好的数据,如图11(i)和(j)所示。

?图11:(a)和(b)计算机生成的连续相位图像。(c) &(d)包裹的相位图像。使用(e)和(f)Itoh算法展开图像:第一种方法,(g)和(h)Itoh方法:第二种方法。继续。。。
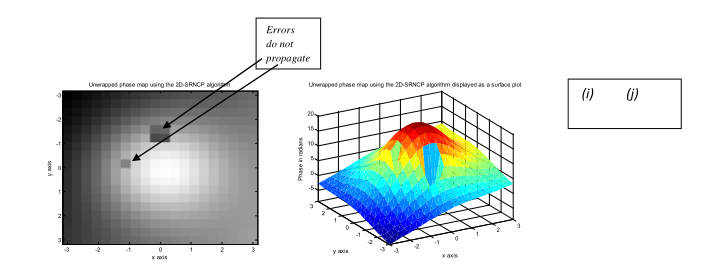
图11:续(i)和(j)2D-SRNCP算法。这里,我们使用的是最低采样率,低于理论上的最小允许极限,NRx=20,NRy=18?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 简单理解自动驾驶-看这篇够了!
- 3_并发编程可见性(volatile)之缓存锁内存屏障过程
- 英飞凌TC3xx之一起认识GTM(十二)详细说说GTM子模块ATOM(概述)
- 回顾2023在CSDN的足迹与2024展望
- java多线程面试集合(1)
- CrawlSpider【获取当前访问链接的父链接和锚文本】代码逻辑
- HarmoryOS Ability页面的生命周期
- Seatunnel MYSQL数据同步
- Python3.5如何打包编译
- UE5 运行时替换角色皮肤