如何用克鲁斯卡尔算法求解最小生成树?
一、克鲁斯卡尔(Kruskal)概述
克鲁斯卡尔(Kruskal)算法也是求连通网的最小生成树的另一种方法。
关于最小生成树相关概念不了解的可以看——Prim算法:如何快速求解最小生成树?-CSDN博客
克鲁斯算法重点需要解决以下问题:
- 对图的所有边按照权值大小进行排序。
- 将边添加到最小生成树时,如果当前最小权值的这条边添加进去,没有导致形成回路,那么就把边添加进树中。否则,不将边添加进树中,继续遍历下一条边。
Kruskal算法和Prim算法有什么区别?
Kruskal算法是基于边进行的贪心算法,而Prim算法是基于节点进行的贪心算法。
在时间复杂度方面,Kruskal算法的时间复杂度为O(ElogE),而Prim算法是O(ElogV),其中E为边,V为顶点
二、克鲁斯卡尔(Kruskal)的基本思路
下面就根据一个修路问题根据上面两点模拟一下克鲁斯卡尔解题的基本思路,根据Kruskal算法找出下面图的最小生成树
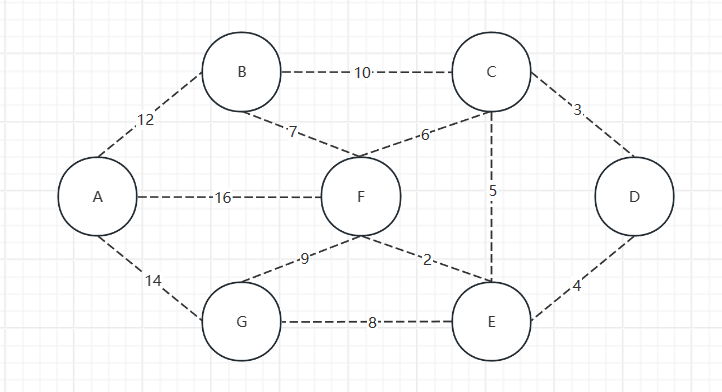
首先,收集图中的边进行排序,这里的话就不做了,因为我们一眼就能看出来。
然后找出权值最小的边,如果将这条边添加到集合中不会导致形成环,则将这个边收集起来,可见,这里权值最小的边为EF。

接着,重复上述步骤,从除去CD的边外,找到最小权值并不形成环的边收集,继续收集CD
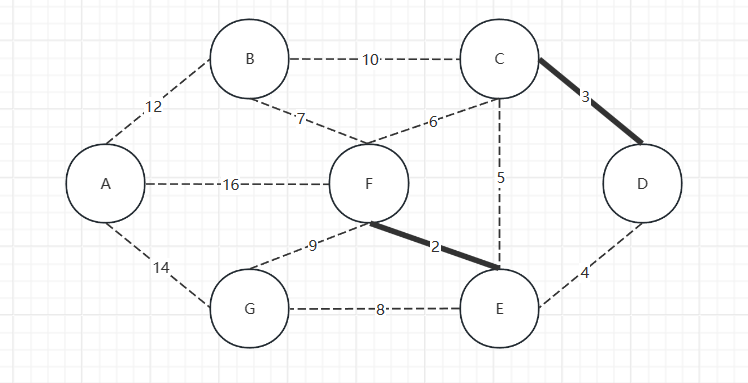
重复上述步骤,收集DE

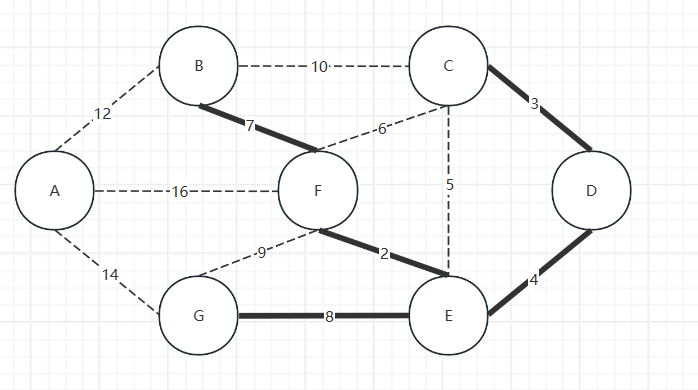
接下来就要注意了,除了CD EF ED三条边外,最小的边就是CE,但是收集CE会导致出现环,于是放弃收集CE。
考虑收集CF,由于CF收集后也会导致环,于是放弃CF,收集BF,BF满足算法思路。

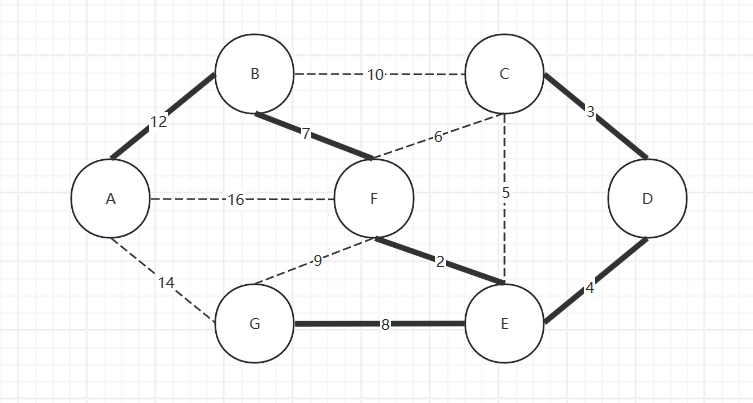
以下就是最后收集到的最小生成树。

三、克鲁斯卡尔(Kruskal)实战
了解了思路之后,就需要进行实战操作了,同样的针对1584. 连接所有点的最小费用 - 力扣(LeetCode)使用Kruskal算法进行解决。
为了保证生成树不包含环,这里需要使用Union-Find 算法,下面先简单介绍一下。
(一)并查集(Union-Find)算法
并查集数据结构(也称为联合-查找数据结构或合并-查找集)基于数组实现的一种跟踪元素的数据结构,这些元素被划分为多个不相交(非重叠)的子集。
它提供了近乎恒定的时间操作(以逆阿克曼函数为界)来添加新集合、合并现有集合以及确定元素是否在同一个集合中。除了推荐算法、好友关系链、族谱等,并查集在的算法中扮演着关键角色,用于寻找无向边加权图的最小生成树。

上面引用了小傅哥的文章——考你个并查集,你竟然抠脚! - 掘金 (juejin.cn),有兴趣可以自己看看。
我就用上面图的案例介绍一下怎么使用Union-Find算法找出是否会形成环。
假如现在打算将顶点5和顶点8相连,那么我们可以根据数据找到顶点5和顶点8各自的父节点。
由数组可知,顶点5的父节点是顶点3,顶点8的父节点是顶点7
同理可推顶点3的父节点是顶点1,顶点7的父节点是顶点6
继续推,顶点1的父节点是顶点6。
这说明顶点5与顶点8是存在相连的路径的,如果顶点5与顶点8直接相连,那么肯定会形成环。
(二)力扣解题思路
- 定义一个对象
Edge表示边,算法开始之前初始化一个Edge集合,存储的是每一条边的顶点和边长度 - 并且初始化一个并查集数据结构,集合中index为i的位置存储的是i,这表示每个节点的父节点都是自己,说明没有相连。
- 将收集到的
Edge边按照边长度从小到大进行排序 - 遍历每一条边,找到这条边两个顶点对应的父节点,如果他们的父节点不相同,说明将这条边收集也不会形成环
- 收集每一条边的同时,收集结果
res,并且给顶点a赋值一个新的父节点b,顺序调转过来也没关系。 - 遍历完成后,
res就是最小费用结果了。
class Solution {
/**
* 交并集的根节点集合
*/
List<Integer> path = new ArrayList<>();
/**
* 边
*/
class Edge {
int a;
int b;
int length;
public Edge(int a, int start, int length) {
this.a = a;
this.b = start;
this.length = length;
}
}
public int minCostConnectPoints(int[][] points) {
int res = 0;
List<Edge> edgeList = new ArrayList<>();
for (int i = 0; i < points.length; i++) {
path.add(i);
for (int j = i + 1; j < points.length; j++) {
int length = Math.abs(points[i][0] - points[j][0]) + Math.abs(points[i][1] - points[j][1]);
edgeList.add(new Edge(i, j, length));
}
}
// 进行排序,从小到大开始排
edgeList.sort((e1, e2) -> e1.length - e2.length);
// 遍历每一条边
for (Edge edge : edgeList) {
int a = find(edge.a), b = find(edge.b);
if (a != b){
// a 和 b不属于同一个父节点,那么可以相连
path.set(a,b);
res += edge.length;
}
}
return res;
}
private int find(int index) {
// 从集合中获取index对应的value
Integer value = path.get(index);
// 如果value不等于index,说明index与另外一个节点相连,于是递归找另外一个节点的父节点
if (value != index){
path.set(index, find(value));
}
return path.get(index);
}
}
参考:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- vue:状态管理库及其部分原理(Vuex、Pinia)
- PyQt6 基类QObject类介绍以及应用
- uniCloud 云数据库(2)
- 第十一站:多态练习ODU
- 2024.1.16 用户画像day01 - 项目介绍
- 推荐一款图集打包工具,png图片打包plist工具,手把手教你使用pngPackerGUI_V2.0
- Centos 7 单机部署 consul
- 【UnityShader入门精要学习笔记】第三章(2)Unity Shader的形式
- C++(Linux下搭建Nginx环境)
- C++——简介、Hello World、变量常量、数据类型