Polynomial(Linear) Regression 多项式线性回归
发布时间:2023年12月19日
介绍:
多项式线性回归是一种线性回归的扩展,它允许我们在模型中使用多项式函数来拟合数据。
线性回归模型假设因变量与自变量之间存在线性关系,即通过一个直线来拟合数据。但是,在某些情况下,数据可能不适合使用直线来拟合,可能需要更复杂的模型。
多项式线性回归就是一种通过多项式函数来拟合数据的方法。它通过引入多项式的高次项来增加模型的复杂度,使其能够更好地拟合非线性的数据。
多项式线性回归模型的一般形式为: y = b0 + b1x + b2x^2 + ... + bn*x^n
其中,y是因变量,x是自变量,b0、b1、...、bn是回归系数,n是多项式的阶数。
多项式线性回归的步骤与普通线性回归相似。首先,需要收集训练数据。然后,选择适当的多项式阶数,并使用最小二乘法或其他方法拟合多项式线性回归模型。最后,可以使用模型进行预测和分析。
多项式线性回归的优点是可以适用于非线性数据,并且具有较强的拟合能力。然而,它也存在一些问题,如过拟合和高次项的数量选择问题。因此,在应用多项式线性回归模型时,需要注意选择合适的模型复杂度,并进行模型评估和调整。
总之,多项式线性回归是一种扩展了线性回归模型的方法,通过引入多项式函数来拟合非线性数据。它是一个强大的工具,可以在多种实际问题中使用。
可以参考一元线性回归:Linear Regression线性回归(一元、多元)-CSDN博客
一、数据处理
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = pd.read_csv('Salary_dataset.csv')
'''结果:
Unnamed: 0 YearsExperience Salary
0 0 1.2 39344
1 1 1.4 46206
2 2 1.6 37732
3 3 2.1 43526
4 4 2.3 39892
5 5 3.0 56643
6 6 3.1 60151
7 7 3.3 54446
8 8 3.3 64446
9 9 3.8 57190
10 10 4.0 63219
11 11 4.1 55795
12 12 4.1 56958
13 13 4.2 57082
14 14 4.6 61112
15 15 5.0 67939
16 16 5.2 66030
17 17 5.4 83089
18 18 6.0 81364
19 19 6.1 93941
20 20 6.9 91739
21 21 7.2 98274
22 22 8.0 101303
23 23 8.3 113813
24 24 8.8 109432
25 25 9.1 105583
26 26 9.6 116970
27 27 9.7 112636
28 28 10.4 122392
29 29 10.6 121873
'''
X=data.iloc[:,1:2].values#自变量
y=data.iloc[:,-1].values#因变量
'''结果:
X array([[ 1.2],
[ 1.4],
[ 1.6],
[ 2.1],
[ 2.3],
[ 3. ],
[ 3.1],
[ 3.3],
[ 3.3],
[ 3.8],
[ 4. ],
[ 4.1],
[ 4.1],
[ 4.2],
[ 4.6],
[ 5. ],
[ 5.2],
[ 5.4],
[ 6. ],
[ 6.1],
[ 6.9],
[ 7.2],
[ 8. ],
[ 8.3],
[ 8.8],
[ 9.1],
[ 9.6],
[ 9.7],
[10.4],
[10.6]])
y array([ 39344, 46206, 37732, 43526, 39892, 56643, 60151, 54446,
64446, 57190, 63219, 55795, 56958, 57082, 61112, 67939,
66030, 83089, 81364, 93941, 91739, 98274, 101303, 113813,
109432, 105583, 116970, 112636, 122392, 121873], dtype=int64)
'''?二、数据分为训练集和测试集
from sklearn.model_selection import train_test_split#将数据分成测试和训练集
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=0)#测试集占百分之二十,random_state=0随机抽取数据集里的成为测试集
X_train.shape
#结果:(24, 1)
X_test.shape
#结果:(6, 1)?三、建模
3.1一元线性回归
from sklearn.linear_model import LinearRegression
LinReg=LinearRegression()#是个类
LinReg.fit(X_train,y_train)#训练集给到这个模型
y_predict=LinReg.predict(X_test)#测试集的预测值
from sklearn.metrics import r2_score
score1=r2_score(y_test,y_predict)#测试集值和预测值进行评估
#结果:0.988169515729126
plt.scatter(X_train,y_train,color='green')#训练集的点
plt.plot(X_test,LinReg.predict(X_test),color='blue')#测试集的线
plt.plot(X_train,LinReg.predict(X_train),color='red')#训练集的线
plt.title('Linear Regressin')
plt.xlabel('YearsExperience')
plt.ylabel('Salary')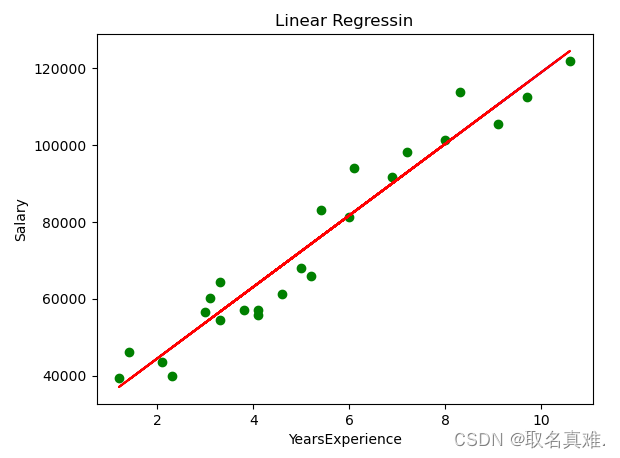
3.2 多项式线性回归
from sklearn.preprocessing import PolynomialFeatures
polynom = PolynomialFeatures(degree=2)#到几次方,0,1,2次方,可以经过调参调整模型的值
X_polynom=polynom.fit_transform(X_train)#拟合数据,转化为标准形式
'''结果:
array([[ 1. , 9.7 , 94.09],
[ 1. , 4.1 , 16.81],
[ 1. , 5.4 , 29.16],
[ 1. , 8. , 64. ],
[ 1. , 3. , 9. ],
[ 1. , 5.2 , 27.04],
[ 1. , 3.3 , 10.89],
[ 1. , 4.6 , 21.16],
[ 1. , 8.3 , 68.89],
[ 1. , 6.9 , 47.61],
[ 1. , 1.4 , 1.96],
[ 1. , 10.6 , 112.36],
[ 1. , 3.1 , 9.61],
[ 1. , 2.3 , 5.29],
[ 1. , 6. , 36. ],
[ 1. , 6.1 , 37.21],
[ 1. , 3.8 , 14.44],
[ 1. , 3.3 , 10.89],
[ 1. , 9.1 , 82.81],
[ 1. , 2.1 , 4.41],
[ 1. , 1.2 , 1.44],
[ 1. , 7.2 , 51.84],
[ 1. , 5. , 25. ],
[ 1. , 4.1 , 16.81]])
'''
PolyReg= LinearRegression()
PolyReg.fit(X_polynom,y_train)#训练集赋给线性回归函数
plt.scatter(X_train,y_train,color='green')#训练集的点
plt.plot(X_test,PolyReg.predict(polynom.fit_transform(X_test)),color='blue')#测试集的线
#plt.plot(X_train,PolyReg.predict(polynom.fit_transform(X_train)),color='red')#训练集的线
plt.title('Linear Regressin')
plt.xlabel('YearsExperience')
plt.ylabel('Salary')
y_predict_pr=PolyReg.predict(polynom.fit_transform(X_test))
r_square = metrics.r2_score(y_test,y_predict_pr)
r_square
#结果:0.9882197351491804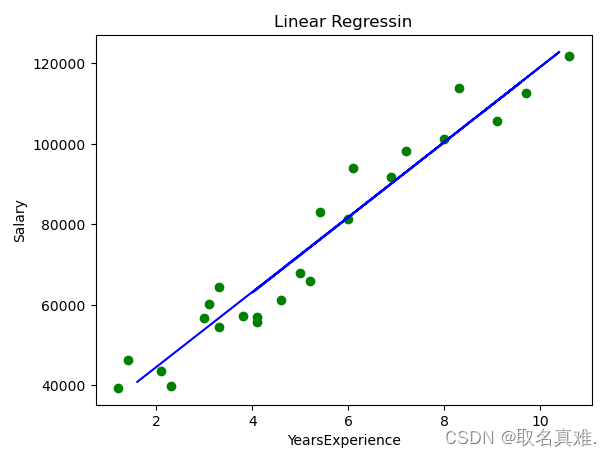
?3.3对比一元线性回归和多项式回归的模型值
y_predict_slr = LinReg.predict(X_test)
from sklearn import metrics
r_square = metrics.r2_score(y_test,y_predict_slr)
r_square
#一元线性回归:0.988169515729126
y_predict_pr=PolyReg.predict(polynom.fit_transform(X_test))
r_square = metrics.r2_score(y_test,y_predict_pr)
r_square
#多项式线性回归:0.9882197351491804
#多项式线性回归模型的值优与一元线性回归
文章来源:https://blog.csdn.net/qq_74156152/article/details/135073106
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 八大常见位运算总结(非常经典,建议收藏)
- 错题总结五
- 前端学习之旅(六)【定位元素居中】
- [Android] 如何在Android中执行自己编译的可执行文件
- 【机器学习】实验记录工具
- 听觉障碍应该找哪些专业人士?如何获得这些职业?
- Java商城免 费 搭 建:VR全景到SAAS,各种模式一网打尽!
- 图像分类(手把手教你搭建分类模型)
- 【C++进阶04】STL中map、set、multimap、multiset的介绍及使用
- 【备战蓝桥杯】——Day1