【C++】AVL树

目录

AVL树的介绍

AVL树的优缺点

全部代码

AVL树的模拟实现

AVLTreeNode的实现

AVLTree的模拟实现

私有成员部分

使用根节点指针作为AVL树的私有成员变量

私有成员函数

公有成员部分

inser接口的实现

旋转图

---

AVL树的介绍

• AVL是一种自平衡二叉搜索树，它的名称来自于它的发明者 Adelson-Velsky 和 Landis 的名字缩写。

• AVL树的性质是，任何一个节点的左右子树高度差不超过1，即AVL树的左右子树高度差的绝对值不超过1。

• AVL树的插入、删除操作都需要通过旋转来保持平衡。旋转分为两种：左旋和右旋。

1. 左旋是指将某个节点的右子树提升到该节点的位置，而右子树的左子树则成为该节点的右子树；

2. 右旋则是将某个节点的左子树提升到该节点的位置，而左子树的右子树则成为该节点的左子树。

3. 通过旋转操作可以保持树的平衡，使得AVL树的高度始终保持在O(log n)。

AVL树的优缺点

• AVL树的优点在于，由于它是一棵高度平衡的树，因此查找、插入、删除等操作都具有较好的时间复杂度保证。

• AVL树的缺点在于，由于维护平衡需要频繁地进行旋转操作，因此在插入、删除等操作时需要付出更高的代价，同时也需要占用更多的内存空间。

全部代码

template<class?T>
struct?AVLTreeNode
{
public:
?AVLTreeNode(const?T&?data?=?T())
??:_cleft(nullptr)
??,?_cright(nullptr)
??,?_parent(nullptr)
??,?_bf(0)
??,?_data(data)
?{}
public:
?AVLTreeNode<T>*?_cleft;
?AVLTreeNode<T>*?_cright;
?AVLTreeNode<T>*?_parent;
?T?_data;
?int?_bf;
};

template<class?T>
class?AVLTree
{
?typedef?AVLTreeNode<T>?Node;
public:
?AVLTree()
??:_root(nullptr)
?{}

?bool?Insert(const?T&?data)
?{
??if?(_root?==?nullptr)
??{
???_root?=?new?Node(data);
???return?true;
??}
??Node*?cur?=?_root;
??Node*?parent?=?nullptr;

??while?(cur?!=?nullptr)
??{
???if?(cur->_data?==?data)
????return?false;
???//寻找插入位置，parent记录父亲节点
???parent?=?cur;
???if?(data?>?cur->_data)
????cur?=?parent->_cright;
???else?if?(data?<?cur->_data)
????cur?=?parent->_cleft;
??}

??//插入逻辑

??if?(data?>?parent->_data)
??{
???parent->_cright?=?new?Node(data);
???cur?=?parent->_cright;
??}
??else?if?(data?<?parent->_data)
??{
???parent->_cleft?=?new?Node(data);
???cur?=?parent->_cleft;
??}
??cur->_parent?=?parent;

??//判断是否需要旋转
??while?(parent)
??{
???//判断插入后对平衡因子的影响
???if?(cur?==?parent->_cleft)
????parent->_bf--;
???else
????parent->_bf++;

???//开始调整平衡因子
???//当插入后parent为0，代表左右子树都有，无需调整
???//当插入后parent为1?-1?代表着高度改变，需要一直调整到根
???//当插入后parent为2?-2?代表着失衡，需要旋转
???if?(parent->_bf?==?0)
????break;
???else?if?(abs(parent->_bf)?==?1)
???{
????cur?=?parent;
????parent?=?cur->_parent;
???}
???else?if?(abs(parent->_bf)?==?2)
???{
????//等于2代表右子树更高
????if?(parent->_bf?==?2)
????{
?????Node*?subr?=?parent->_cright;
?????if?(subr->_bf?==?1)//插在右子树的右的树上
?????{
??????_RotateL(parent);
?????}
?????else?if?(subr->_bf?==?-1)//插在右子树的左树上
?????{
??????_RotateRL(parent);
?????}
????}
????else?if?(parent->_bf?==?-2)
????{
?????Node*?subl?=?parent->_cleft;
?????if?(subl->_bf?==?-1)
?????{
??????_RotateR(parent);
?????}
?????else?if?(subl->_bf?==?1)
?????{
??????_RotateLR(parent);
?????}
????}
????break;
???}
??}
??return?true;
?}

?void?inprint()
?{
??_inprint(_root);
?}

?void?prevprint()
?{
??_prevprint(_root);
?}

?int?Height()
?{
??return?_Height(_root);
?}

?bool?IsBalanceTree()
?{
??return?_IsBalanceTree(_root);
?}
private:

?int?_Height(Node*?root)
?{
??if?(root?==?nullptr)
???return?0;

??int?leftHigh?=?_Height(root->_cleft);
??int?rightHigh?=?_Height(root->_cright);
??int?max1?=?max(leftHigh,?rightHigh);

??return?1?+?max1;
?}
?void?_inprint(Node*?root)
?{
??if?(root?==?nullptr)
???return;

??_inprint(root->_cleft);
??cout?<<?root->_data?<<?'?';
??_inprint(root->_cright);
?}

?void?_prevprint(Node*?root)
?{
??if?(root?==?nullptr)
???return;
??cout?<<?root->_data?<<?'?';
??_prevprint(root->_cleft);
??_prevprint(root->_cright);
?}

?void?_RotateL(Node*?parent)
?{
??Node*?subR?=?parent->_cright;
??Node*?subRL?=?subR->_cleft;

??parent->_cright?=?subRL;
??if?(subRL)//防止右子树的左树为空
???subRL->_parent?=?parent;

??subR->_cleft?=?parent;

??Node*?pparent?=?parent->_parent;
??parent->_parent?=?subR;

??subR->_parent?=?pparent;
??if?(pparent?==?nullptr)
???_root?=?subR;
??else
??{
???if?(parent?==?pparent->_cleft)
????pparent->_cleft?=?subR;
???else
????pparent->_cright?=?subR;
??}
??subR->_bf?=?0;
??parent->_bf?=?0;
?}

?void?_RotateR(Node*?parent)
?{
??Node*?subL?=?parent->_cleft;
??Node*?subLR?=?subL->_cright;

??parent->_cleft?=?subLR;
??if?(subLR)
???subLR->_parent?=?parent;

??subL->_cright?=?parent;

??//parent可能是一颗子树，先保存其双亲节点
??Node*?pparent?=?parent->_parent;

??parent->_parent?=?subL;
??subL->_parent?=?pparent;
??if?(pparent?==?nullptr)//parent为根节点情况
???_root?=?subL;
??else
??{
???if?(parent?==?pparent->_cleft)
????pparent->_cleft?=?subL;
???else
????pparent->_cright?=?subL;
??}
??parent->_bf?=?subL->_bf?=?0;
?}

?//右左双旋
?void?_RotateRL(Node*?parent)
?{
??Node*?subR?=?parent->_cright;
??Node*?subRL?=?subR->_cleft;

??int?tmp?=?subRL->_bf;

??_RotateR(parent->_cright);
??_RotateL(parent);

??if?(tmp?==?0)
??{
???//?subRL自己就是新增
???parent->_bf?=?subR->_bf?=?subRL->_bf?=?0;
??}
??else?if?(tmp?==?-1)
??{
???//?subRL的左子树新增
???parent->_bf?=?0;
???subRL->_bf?=?0;
???subR->_bf?=?1;
??}
??else?if?(tmp?==?1)
??{
???//?subRL的右子树新增
???parent->_bf?=?-1;
???subRL->_bf?=?0;
???subR->_bf?=?0;
??}
??else
??{
???assert(false);
??}
?}

?void?_RotateLR(Node*?parent)
?{
??Node*?subL?=?parent->_cleft;
??Node*?subLR?=?subL->_cright;

??int?tmp?=?subLR->_bf;

??_RotateL(parent->_cleft);
??_RotateR(parent);

??if?(tmp?==?0)
??{
???//?subRL自己就是新增
???parent->_bf?=?subL->_bf?=?subLR->_bf?=?0;
??}
??else?if?(tmp?==?-1)
??{
???//?subRL的左子树新增
???parent->_bf?=?0;
???subLR->_bf?=?0;
???subL->_bf?=?1;
??}
??else?if?(tmp?==?1)
??{
???//?subRL的右子树新增
???parent->_bf?=?-1;
???subLR->_bf?=?0;
???subL->_bf?=?0;
??}
??else
??{
???assert(false);
??}
?}

?bool?_IsBalanceTree(Node*?root)
?{
??if?(root?==?nullptr)
???return?true;

??int?leftHeight?=?_Height(root->_cleft);
??int?rightHeight?=?_Height(root->_cright);
??int?sub?=?rightHeight?-?leftHeight;
??if?(sub?!=?root->_bf?||?sub?>?1)
???return?false;

??return?_IsBalanceTree(root->_cleft)?&&?_IsBalanceTree(root->_cright);
?}
private:
?Node*?_root;
};

AVL树的模拟实现

AVLTreeNode的实现

• AVLTreeNode结构定义了AVL树的节点，每个节点包含了左子节点、右子节点、父节点的指针，以及节点的数据和平衡因子。通过这些成员变量，可以构建AVL树的数据结构。

• 成员变量：

1. _cleft：指向左子节点的指针。

2. _cright：指向右子节点的指针。

3. _parent：指向父节点的指针。

4. _data：存储节点数据的变量，类型为T。

5. _bf：用于记录平衡因子的变量，表示左右子树高度差。

• 构造函数：AVLTreeNode(const T& data = T())：构造函数，可以传入一个参数data，默认值为T类型的默认值。在构造节点时，会初始化成员变量，并将传入的data赋值给_data。

template<class?T>
struct?AVLTreeNode
{
public:
?AVLTreeNode(const?T&?data?=?T())
??:_cleft(nullptr)
??,?_cright(nullptr)
??,?_parent(nullptr)
??,?_bf(0)
??,?_data(data)
?{}
public:
?AVLTreeNode<T>*?_cleft;
?AVLTreeNode<T>*?_cright;
?AVLTreeNode<T>*?_parent;
?T?_data;
?int?_bf;
};

AVLTree的模拟实现

• 仅实现了插入、前中序遍历、测量高度等几个功能

template<class?T>
class?AVLTree
{
?typedef?AVLTreeNode<T>?Node;
public:
?AVLTree()
??:_root(nullptr)
?{}

?bool?Insert(const?T&?data)
?{
??if?(_root?==?nullptr)
??{
???_root?=?new?Node(data);
???return?true;
??}
??Node*?cur?=?_root;
??Node*?parent?=?nullptr;

??while?(cur?!=?nullptr)
??{
???if?(cur->_data?==?data)
????return?false;
???//寻找插入位置，parent记录父亲节点
???parent?=?cur;
???if?(data?>?cur->_data)
????cur?=?parent->_cright;
???else?if?(data?<?cur->_data)
????cur?=?parent->_cleft;
??}

??//插入逻辑

??if?(data?>?parent->_data)
??{
???parent->_cright?=?new?Node(data);
???cur?=?parent->_cright;
??}
??else?if?(data?<?parent->_data)
??{
???parent->_cleft?=?new?Node(data);
???cur?=?parent->_cleft;
??}
??cur->_parent?=?parent;

??//判断是否需要旋转
??while?(parent)
??{
???//判断插入后对平衡因子的影响
???if?(cur?==?parent->_cleft)
????parent->_bf--;
???else
????parent->_bf++;

???//开始调整平衡因子
???//当插入后parent为0，代表左右子树都有，无需调整
???//当插入后parent为1?-1?代表着高度改变，需要一直调整到根
???//当插入后parent为2?-2?代表着失衡，需要旋转
???if?(parent->_bf?==?0)
????break;
???else?if?(abs(parent->_bf)?==?1)
???{
????cur?=?parent;
????parent?=?cur->_parent;
???}
???else?if?(abs(parent->_bf)?==?2)
???{
????//等于2代表右子树更高
????if?(parent->_bf?==?2)
????{
?????Node*?subr?=?parent->_cright;
?????if?(subr->_bf?==?1)//插在右子树的右的树上
?????{
??????_RotateL(parent);
?????}
?????else?if?(subr->_bf?==?-1)//插在右子树的左树上
?????{
??????_RotateRL(parent);
?????}
????}
????else?if?(parent->_bf?==?-2)
????{
?????Node*?subl?=?parent->_cleft;
?????if?(subl->_bf?==?-1)
?????{
??????_RotateR(parent);
?????}
?????else?if?(subl->_bf?==?1)
?????{
??????_RotateLR(parent);
?????}
????}
????break;
???}
??}
??return?true;
?}

?void?inprint()
?{
??_inprint(_root);
?}

?void?prevprint()
?{
??_prevprint(_root);
?}

?int?Height()
?{
??return?_Height(_root);
?}

?bool?IsBalanceTree()
?{
??return?_IsBalanceTree(_root);
?}
private:

?int?_Height(Node*?root)
?{
??if?(root?==?nullptr)
???return?0;

??int?leftHigh?=?_Height(root->_cleft);
??int?rightHigh?=?_Height(root->_cright);
??int?max1?=?max(leftHigh,?rightHigh);

??return?1?+?max1;
?}
?void?_inprint(Node*?root)
?{
??if?(root?==?nullptr)
???return;

??_inprint(root->_cleft);
??cout?<<?root->_data?<<?'?';
??_inprint(root->_cright);
?}

?void?_prevprint(Node*?root)
?{
??if?(root?==?nullptr)
???return;
??cout?<<?root->_data?<<?'?';
??_prevprint(root->_cleft);
??_prevprint(root->_cright);
?}

?void?_RotateL(Node*?parent)
?{
??Node*?subR?=?parent->_cright;
??Node*?subRL?=?subR->_cleft;

??parent->_cright?=?subRL;
??if?(subRL)//防止右子树的左树为空
???subRL->_parent?=?parent;

??subR->_cleft?=?parent;

??Node*?pparent?=?parent->_parent;
??parent->_parent?=?subR;

??subR->_parent?=?pparent;
??if?(pparent?==?nullptr)
???_root?=?subR;
??else
??{
???if?(parent?==?pparent->_cleft)
????pparent->_cleft?=?subR;
???else
????pparent->_cright?=?subR;
??}
??subR->_bf?=?0;
??parent->_bf?=?0;
?}

?void?_RotateR(Node*?parent)
?{
??Node*?subL?=?parent->_cleft;
??Node*?subLR?=?subL->_cright;

??parent->_cleft?=?subLR;
??if?(subLR)
???subLR->_parent?=?parent;

??subL->_cright?=?parent;

??//parent可能是一颗子树，先保存其双亲节点
??Node*?pparent?=?parent->_parent;

??parent->_parent?=?subL;
??subL->_parent?=?pparent;
??if?(pparent?==?nullptr)//parent为根节点情况
???_root?=?subL;
??else
??{
???if?(parent?==?pparent->_cleft)
????pparent->_cleft?=?subL;
???else
????pparent->_cright?=?subL;
??}
??parent->_bf?=?subL->_bf?=?0;
?}

?//右左双旋
?void?_RotateRL(Node*?parent)
?{
??Node*?subR?=?parent->_cright;
??Node*?subRL?=?subR->_cleft;

??int?tmp?=?subRL->_bf;

??_RotateR(parent->_cright);
??_RotateL(parent);

??if?(tmp?==?0)
??{
???//?subRL自己就是新增
???parent->_bf?=?subR->_bf?=?subRL->_bf?=?0;
??}
??else?if?(tmp?==?-1)
??{
???//?subRL的左子树新增
???parent->_bf?=?0;
???subRL->_bf?=?0;
???subR->_bf?=?1;
??}
??else?if?(tmp?==?1)
??{
???//?subRL的右子树新增
???parent->_bf?=?-1;
???subRL->_bf?=?0;
???subR->_bf?=?0;
??}
??else
??{
???assert(false);
??}
?}

?void?_RotateLR(Node*?parent)
?{
??Node*?subL?=?parent->_cleft;
??Node*?subLR?=?subL->_cright;

??int?tmp?=?subLR->_bf;

??_RotateL(parent->_cleft);
??_RotateR(parent);

??if?(tmp?==?0)
??{
???//?subRL自己就是新增
???parent->_bf?=?subL->_bf?=?subLR->_bf?=?0;
??}
??else?if?(tmp?==?-1)
??{
???//?subRL的左子树新增
???parent->_bf?=?0;
???subLR->_bf?=?0;
???subL->_bf?=?1;
??}
??else?if?(tmp?==?1)
??{
???//?subRL的右子树新增
???parent->_bf?=?-1;
???subLR->_bf?=?0;
???subL->_bf?=?0;
??}
??else
??{
???assert(false);
??}
?}

?bool?_IsBalanceTree(Node*?root)
?{
??if?(root?==?nullptr)
???return?true;

??int?leftHeight?=?_Height(root->_cleft);
??int?rightHeight?=?_Height(root->_cright);
??int?sub?=?rightHeight?-?leftHeight;
??if?(sub?!=?root->_bf?||?sub?>?1)
???return?false;

??return?_IsBalanceTree(root->_cleft)?&&?_IsBalanceTree(root->_cright);
?}
private:
?Node*?_root;
};

私有成员部分

使用根节点指针作为AVL树的私有成员变量

private:
?Node*?_root;

私有成员函数

• 全是辅助性接口

• 旋转操作有四种：左单旋、右单旋、左右双旋、右左双旋，都是insert接口的辅助函数

• 测量高度、判断是否为AVL数、前序和中序遍历接口是为了实现递归检测而写的辅助函数

1. _Height(Node* root)：计算以root为根节点的子树的高度。递归地计算左子树和右子树的高度，并返回较大值加1作为当前节点的高度。

2. _inprint(Node* root)：中序遍历打印以root为根节点的子树。先递归地打印左子树，然后打印当前节点，最后递归地打印右子树。

3. _prevprint(Node* root)：先序遍历打印以root为根节点的子树。先打印当前节点，然后递归地打印左子树，最后递归地打印右子树。

4. _RotateL(Node* parent)：左旋操作，将parent节点向左旋转。具体操作为将parent的右子节点subR提升为根节点，subR的左子节点subRL成为parent的右子节点，parent成为subR的左子节点。

5. _RotateR(Node* parent)：右旋操作，将parent节点向右旋转。具体操作为将parent的左子节点subL提升为根节点，subL的右子节点subLR成为parent的左子节点，parent成为subL的右子节点。

6. _RotateRL(Node* parent)：右左双旋操作，先对parent的右子节点进行右旋操作，再对parent进行左旋操作。

7. _RotateLR(Node* parent)：左右双旋操作，先对parent的左子节点进行左旋操作，再对parent进行右旋操作。

8. _IsBalanceTree(Node* root)：判断以root为根节点的子树是否为平衡二叉树。递归地判断左子树和右子树的高度差是否符合平衡条件，并且判断每个节点的平衡因子是否与高度差一致。

private:

?int?_Height(Node*?root)
?{
??if?(root?==?nullptr)
???return?0;

??int?leftHigh?=?_Height(root->_cleft);
??int?rightHigh?=?_Height(root->_cright);
??int?max1?=?max(leftHigh,?rightHigh);

??return?1?+?max1;
?}
?void?_inprint(Node*?root)
?{
??if?(root?==?nullptr)
???return;

??_inprint(root->_cleft);
??cout?<<?root->_data?<<?'?';
??_inprint(root->_cright);
?}

?void?_prevprint(Node*?root)
?{
??if?(root?==?nullptr)
???return;
??cout?<<?root->_data?<<?'?';
??_prevprint(root->_cleft);
??_prevprint(root->_cright);
?}

?void?_RotateL(Node*?parent)
?{
??Node*?subR?=?parent->_cright;
??Node*?subRL?=?subR->_cleft;

??parent->_cright?=?subRL;
??if?(subRL)//防止右子树的左树为空
???subRL->_parent?=?parent;

??subR->_cleft?=?parent;

??Node*?pparent?=?parent->_parent;
??parent->_parent?=?subR;

??subR->_parent?=?pparent;
??if?(pparent?==?nullptr)
???_root?=?subR;
??else
??{
???if?(parent?==?pparent->_cleft)
????pparent->_cleft?=?subR;
???else
????pparent->_cright?=?subR;
??}
??subR->_bf?=?0;
??parent->_bf?=?0;
?}

?void?_RotateR(Node*?parent)
?{
??Node*?subL?=?parent->_cleft;
??Node*?subLR?=?subL->_cright;

??parent->_cleft?=?subLR;
??if?(subLR)
???subLR->_parent?=?parent;

??subL->_cright?=?parent;

??//parent可能是一颗子树，先保存其双亲节点
??Node*?pparent?=?parent->_parent;

??parent->_parent?=?subL;
??subL->_parent?=?pparent;
??if?(pparent?==?nullptr)//parent为根节点情况
???_root?=?subL;
??else
??{
???if?(parent?==?pparent->_cleft)
????pparent->_cleft?=?subL;
???else
????pparent->_cright?=?subL;
??}
??parent->_bf?=?subL->_bf?=?0;
?}

?//右左双旋
?void?_RotateRL(Node*?parent)
?{
??Node*?subR?=?parent->_cright;
??Node*?subRL?=?subR->_cleft;

??int?tmp?=?subRL->_bf;

??_RotateR(parent->_cright);
??_RotateL(parent);

??if?(tmp?==?0)
??{
???//?subRL自己就是新增
???parent->_bf?=?subR->_bf?=?subRL->_bf?=?0;
??}
??else?if?(tmp?==?-1)
??{
???//?subRL的左子树新增
???parent->_bf?=?0;
???subRL->_bf?=?0;
???subR->_bf?=?1;
??}
??else?if?(tmp?==?1)
??{
???//?subRL的右子树新增
???parent->_bf?=?-1;
???subRL->_bf?=?0;
???subR->_bf?=?0;
??}
??else
??{
???assert(false);
??}
?}

?void?_RotateLR(Node*?parent)
?{
??Node*?subL?=?parent->_cleft;
??Node*?subLR?=?subL->_cright;

??int?tmp?=?subLR->_bf;

??_RotateL(parent->_cleft);
??_RotateR(parent);

??if?(tmp?==?0)
??{
???//?subRL自己就是新增
???parent->_bf?=?subL->_bf?=?subLR->_bf?=?0;
??}
??else?if?(tmp?==?-1)
??{
???//?subRL的左子树新增
???parent->_bf?=?0;
???subLR->_bf?=?0;
???subL->_bf?=?1;
??}
??else?if?(tmp?==?1)
??{
???//?subRL的右子树新增
???parent->_bf?=?-1;
???subLR->_bf?=?0;
???subL->_bf?=?0;
??}
??else
??{
???assert(false);
??}
?}

?bool?_IsBalanceTree(Node*?root)
?{
??if?(root?==?nullptr)
???return?true;

??int?leftHeight?=?_Height(root->_cleft);
??int?rightHeight?=?_Height(root->_cright);
??int?sub?=?rightHeight?-?leftHeight;
??if?(sub?!=?root->_bf?||?sub?>?1)
???return?false;

??return?_IsBalanceTree(root->_cleft)?&&?_IsBalanceTree(root->_cright);
?}

公有成员部分

1. AVLTree构造函数 AVLTree类的默认构造函数，初始化根节点为nullptr。

2. Insert函数 AVLTree的插入函数，将一个新节点插入到树中。

3. inprint函数 对树进行中序遍历打印。

4. prevprint函数 对树进行前序遍历打印。

5. Height函数 计算树的高度，即从根节点到最深叶子节点的路径长度。

6. IsBalanceTree函数 判断是否为AVL树。

public:
?AVLTree()
??:_root(nullptr)
?{}

?bool?Insert(const?T&?data)
?{
??if?(_root?==?nullptr)
??{
???_root?=?new?Node(data);
???return?true;
??}
??Node*?cur?=?_root;
??Node*?parent?=?nullptr;

??while?(cur?!=?nullptr)
??{
???if?(cur->_data?==?data)
????return?false;
???//寻找插入位置，parent记录父亲节点
???parent?=?cur;
???if?(data?>?cur->_data)
????cur?=?parent->_cright;
???else?if?(data?<?cur->_data)
????cur?=?parent->_cleft;
??}

??//插入逻辑

??if?(data?>?parent->_data)
??{
???parent->_cright?=?new?Node(data);
???cur?=?parent->_cright;
??}
??else?if?(data?<?parent->_data)
??{
???parent->_cleft?=?new?Node(data);
???cur?=?parent->_cleft;
??}
??cur->_parent?=?parent;

??//判断是否需要旋转
??while?(parent)
??{
???//判断插入后对平衡因子的影响
???if?(cur?==?parent->_cleft)
????parent->_bf--;
???else
????parent->_bf++;

???//开始调整平衡因子
???//当插入后parent为0，代表左右子树都有，无需调整
???//当插入后parent为1?-1?代表着高度改变，需要一直调整到根
???//当插入后parent为2?-2?代表着失衡，需要旋转
???if?(parent->_bf?==?0)
????break;
???else?if?(abs(parent->_bf)?==?1)
???{
????cur?=?parent;
????parent?=?cur->_parent;
???}
???else?if?(abs(parent->_bf)?==?2)
???{
????//等于2代表右子树更高
????if?(parent->_bf?==?2)
????{
?????Node*?subr?=?parent->_cright;
?????if?(subr->_bf?==?1)//插在右子树的右的树上
?????{
??????_RotateL(parent);
?????}
?????else?if?(subr->_bf?==?-1)//插在右子树的左树上
?????{
??????_RotateRL(parent);
?????}
????}
????else?if?(parent->_bf?==?-2)
????{
?????Node*?subl?=?parent->_cleft;
?????if?(subl->_bf?==?-1)
?????{
??????_RotateR(parent);
?????}
?????else?if?(subl->_bf?==?1)
?????{
??????_RotateLR(parent);
?????}
????}
????break;
???}
??}
??return?true;
?}

?void?inprint()
?{
??_inprint(_root);
?}

?void?prevprint()
?{
??_prevprint(_root);
?}

?int?Height()
?{
??return?_Height(_root);
?}

?bool?IsBalanceTree()
?{
??return?_IsBalanceTree(_root);
?}

inser接口的实现

• 首先判断根节点是否为空，如果为空则直接插入并返回true。

• 如果根节点不为空，则从根节点开始查找要插入的位置，同时记录每个节点的父亲节点。

• 如果找到了相同的数据，则返回false，表示插入失败。

• 如果找到了合适的位置，则在该位置插入新节点，并将该节点的父亲节点指向记录的父亲节点。

• 在插入后需要判断是否需要旋转来维持平衡性，因此需要进行平衡因子的调整。对于新增加的节点cur，如果它插在parent的左边，则parent的平衡因子减1，否则增1。

• 如果parent的平衡因子为0，则代表左右子树都已经有了，无需调整，退出循环；如果parent的平衡因子为1或-1，则代表高度改变，需要继续向上调整；如果parent的平衡因子为2或-2，则代表失衡，需要进行旋转操作。

• 进行旋转操作前，需要判断是进行左旋还是右旋，还是进行左右双旋或右左双旋。具体操作可以参考代码中的注释。

• 最后返回true表示插入成功。

bool?Insert(const?T&?data)
?{
??if?(_root?==?nullptr)
??{
???_root?=?new?Node(data);
???return?true;
??}
??Node*?cur?=?_root;
??Node*?parent?=?nullptr;

??while?(cur?!=?nullptr)
??{
???if?(cur->_data?==?data)
????return?false;
???//寻找插入位置，parent记录父亲节点
???parent?=?cur;
???if?(data?>?cur->_data)
????cur?=?parent->_cright;
???else?if?(data?<?cur->_data)
????cur?=?parent->_cleft;
??}

??//插入逻辑

??if?(data?>?parent->_data)
??{
???parent->_cright?=?new?Node(data);
???cur?=?parent->_cright;
??}
??else?if?(data?<?parent->_data)
??{
???parent->_cleft?=?new?Node(data);
???cur?=?parent->_cleft;
??}
??cur->_parent?=?parent;

??//判断是否需要旋转
??while?(parent)
??{
???//判断插入后对平衡因子的影响
???if?(cur?==?parent->_cleft)
????parent->_bf--;
???else
????parent->_bf++;

???//开始调整平衡因子
???//当插入后parent为0，代表左右子树都有，无需调整
???//当插入后parent为1?-1?代表着高度改变，需要一直调整到根
???//当插入后parent为2?-2?代表着失衡，需要旋转
???if?(parent->_bf?==?0)
????break;
???else?if?(abs(parent->_bf)?==?1)
???{
????cur?=?parent;
????parent?=?cur->_parent;
???}
???else?if?(abs(parent->_bf)?==?2)
???{
????//等于2代表右子树更高
????if?(parent->_bf?==?2)
????{
?????Node*?subr?=?parent->_cright;
?????if?(subr->_bf?==?1)//插在右子树的右的树上
?????{
??????_RotateL(parent);
?????}
?????else?if?(subr->_bf?==?-1)//插在右子树的左树上
?????{
??????_RotateRL(parent);
?????}
????}
????else?if?(parent->_bf?==?-2)
????{
?????Node*?subl?=?parent->_cleft;
?????if?(subl->_bf?==?-1)
?????{
??????_RotateR(parent);
?????}
?????else?if?(subl->_bf?==?1)
?????{
??????_RotateLR(parent);
?????}
????}
????break;
???}
??}
??return?true;
?}

旋转图

• 右单旋 新节点插入较高左子树的左侧

• 左单旋 新节点插入较高右子树的右侧

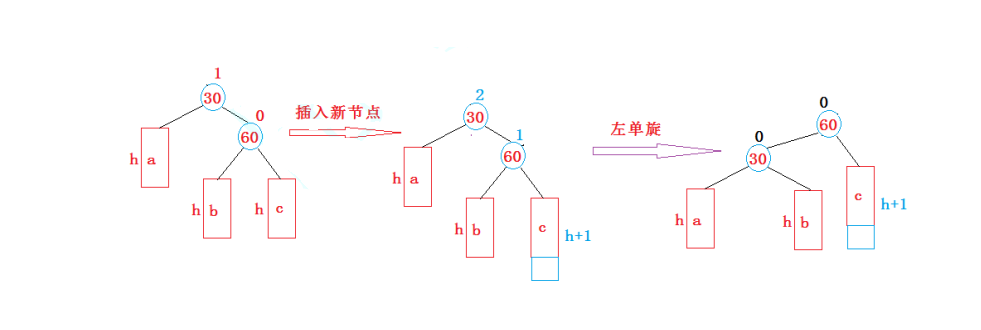
• 左右双旋 新节点插入较高左子树的右侧

• 右左双旋 新节点插入较高右子树的左侧