Fourier transform笔记
https://www.youtube.com/watch?v=spUNpyF58BY
笔记
Fourier transform
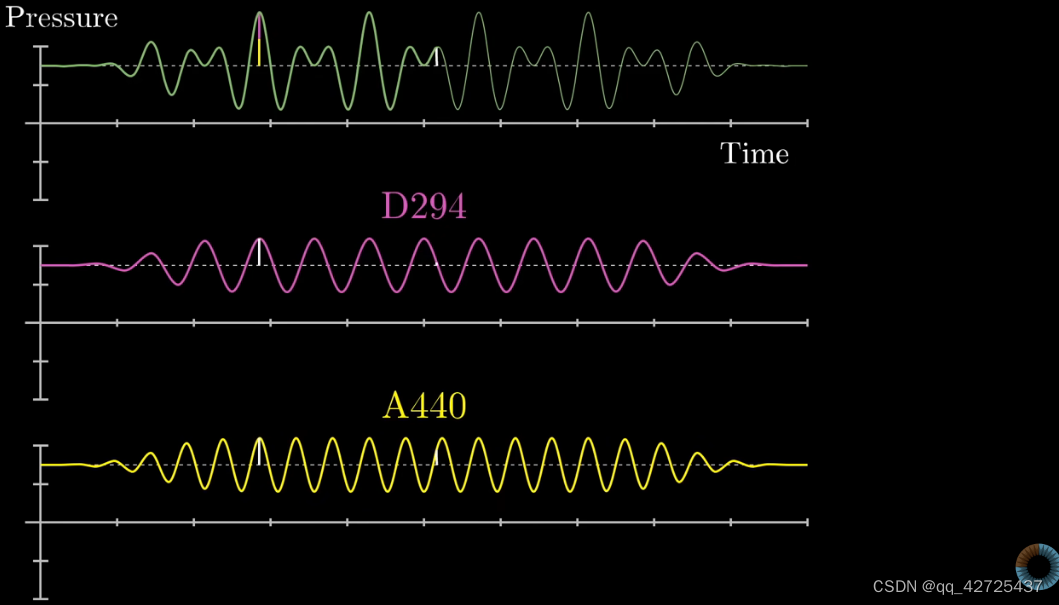
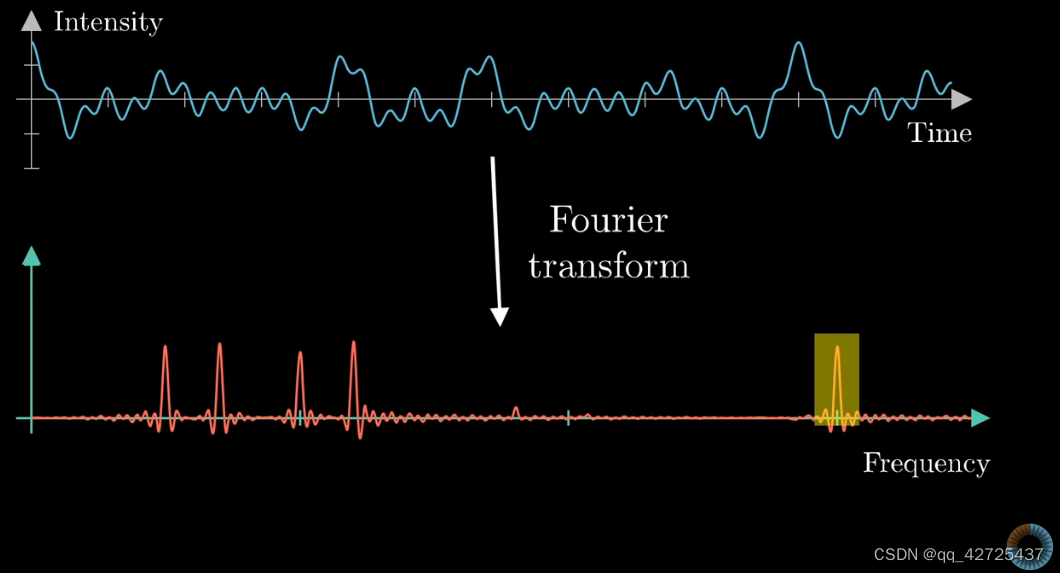
对于一个声音，可以把它拆解为多个正弦波，上面是两个正弦波组成的声波，但是当情况更复杂以后
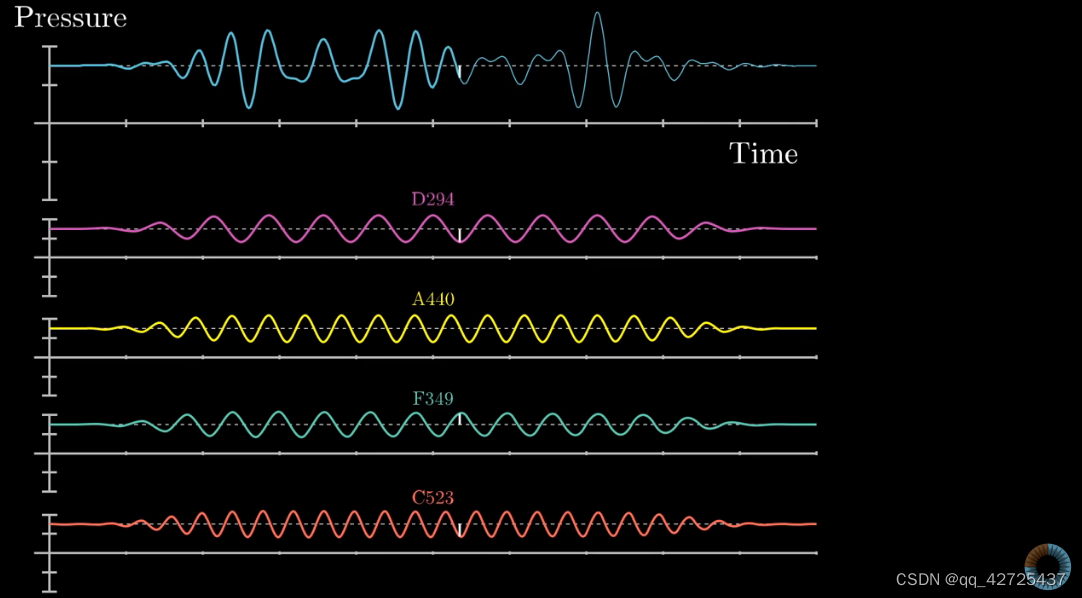
很难，从声波中提取出有用的信息，所以采用下面的方法
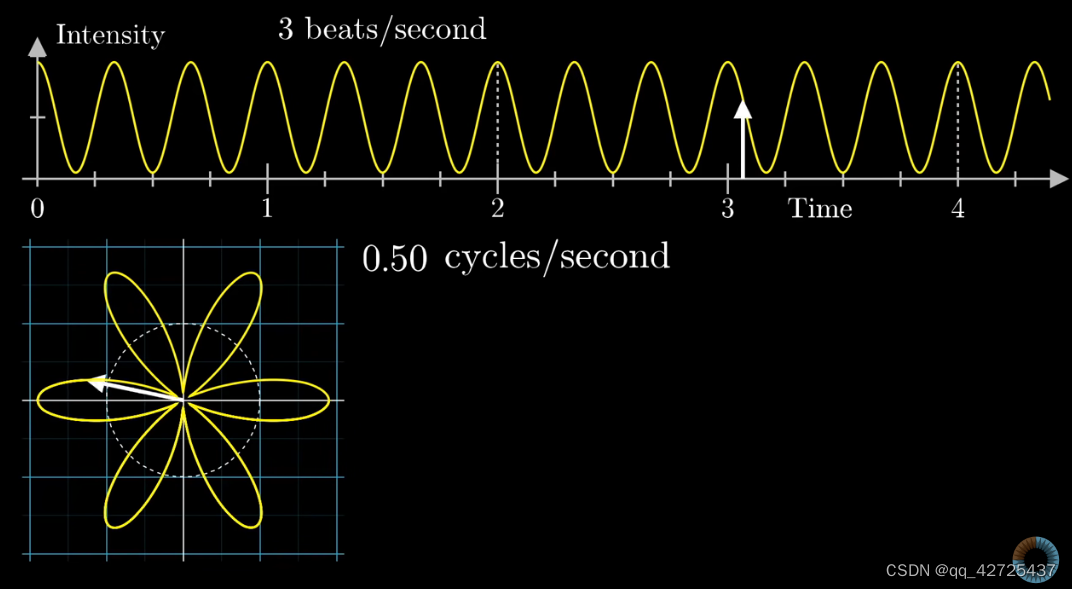
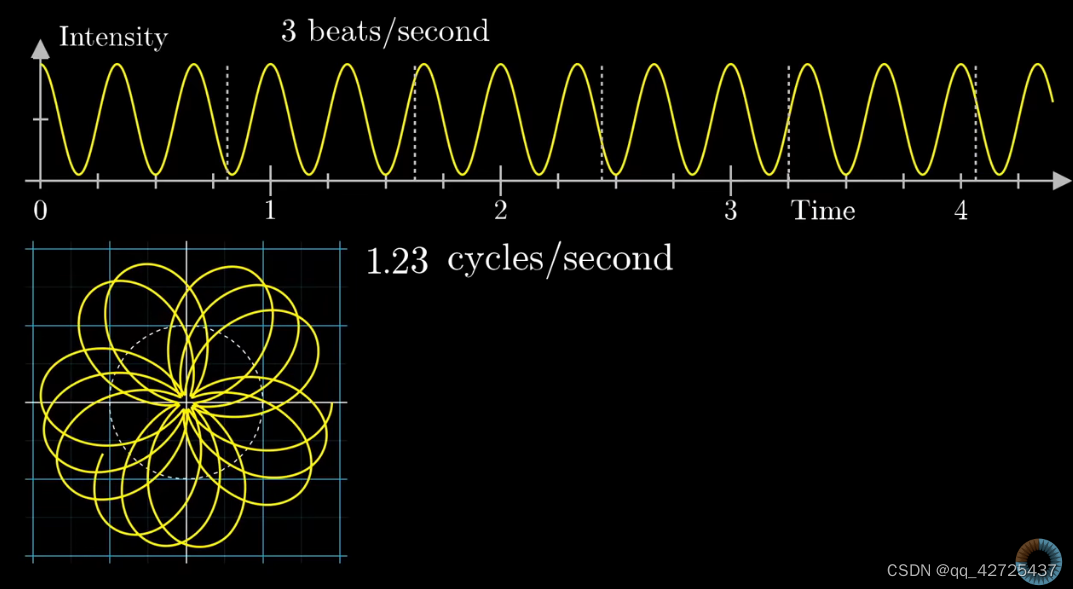
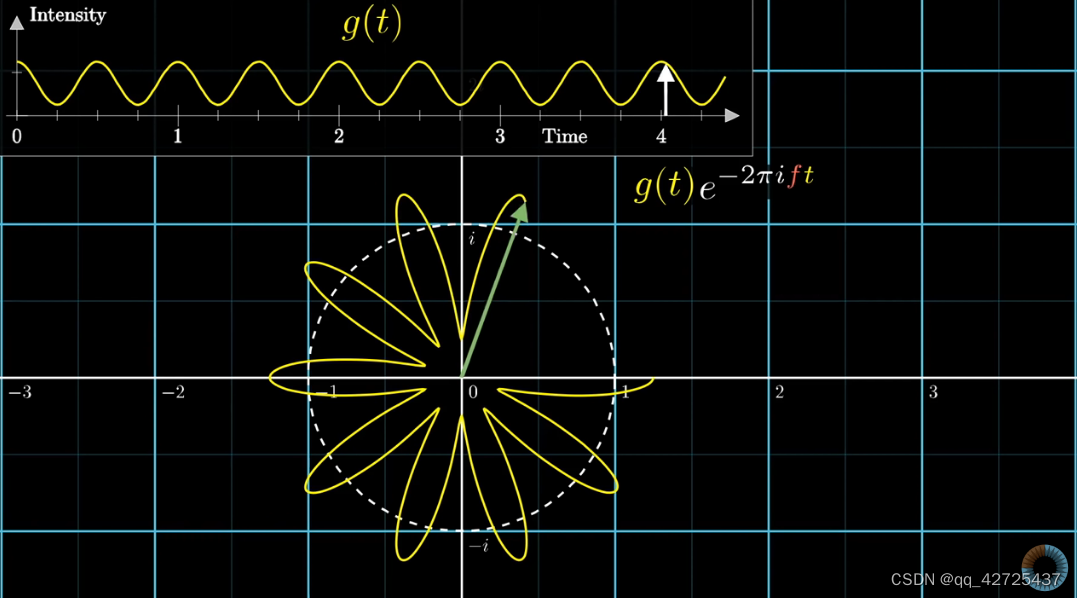
可以看到，将时间上的波形转换为了左下角的环形的波形，其中，与远点的距离与上面图中与时间轴相对应（白色箭头），图中，有两个频率，一个是时间上的频率，一秒内有3个beats，另一个是打包上图得到左下图的频率（图中虚线），这里是0.5c/s，也就是左下图旋转一周，时间上过了2s。不同的频率，得到的图是不同的。
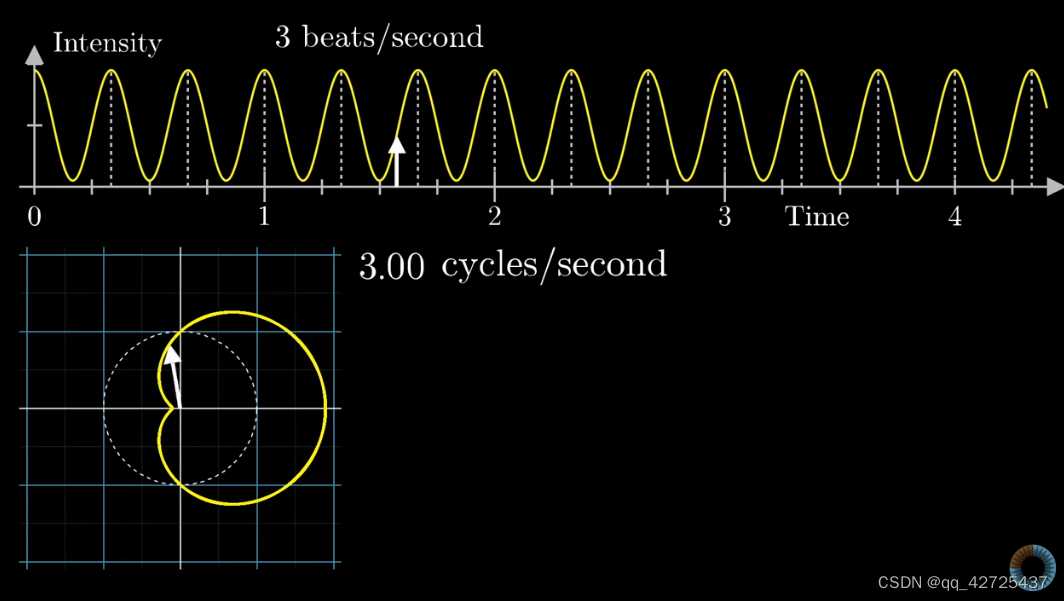
把左下图中的图形当作一个整体，得到质心，绘制出下图，其中右下图中的y轴是左下图质心的x轴坐标信息。
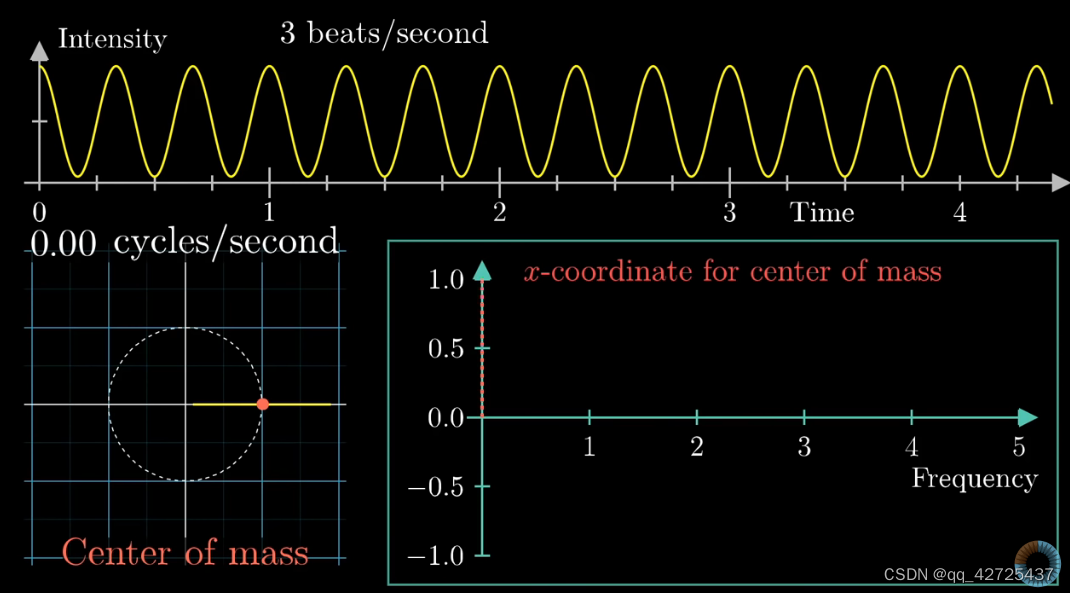
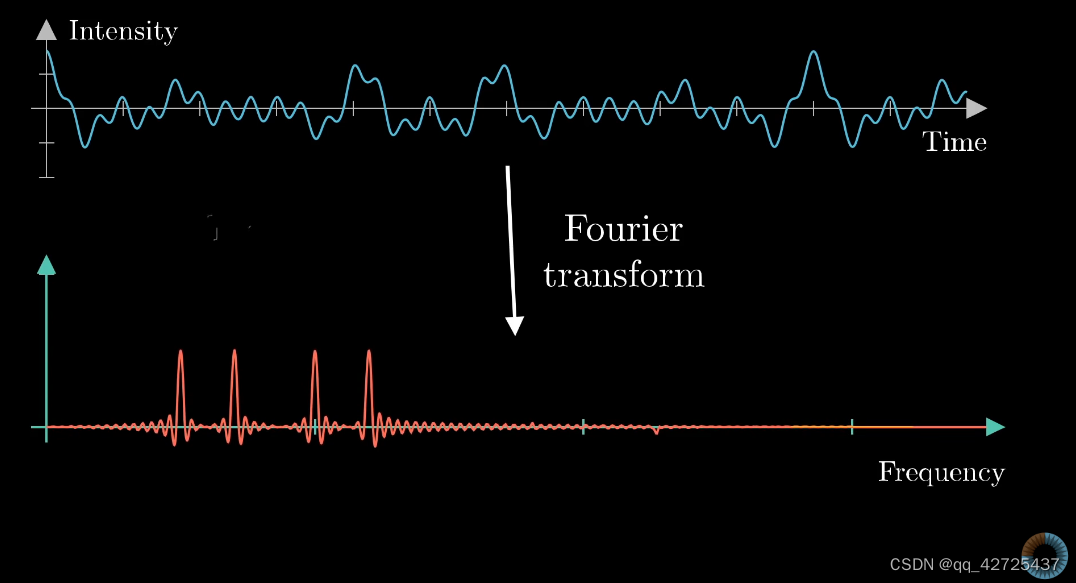
这样就得到了频域的信息，可以看到，在3明显突起，更改幅度，依然如此
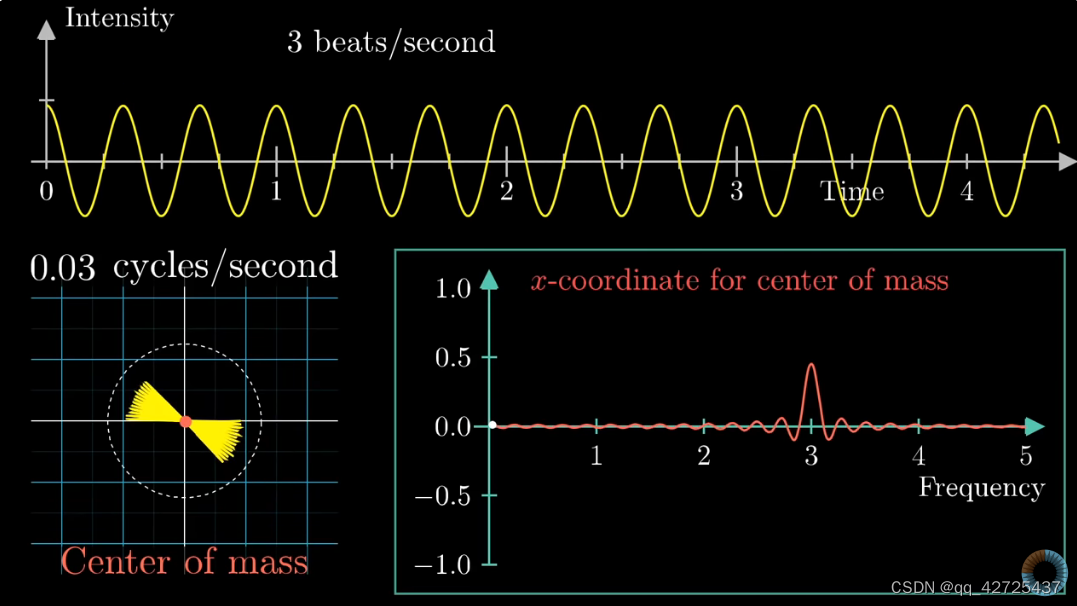
3正好是频率的值，这不是巧合，可以用它来分解波形
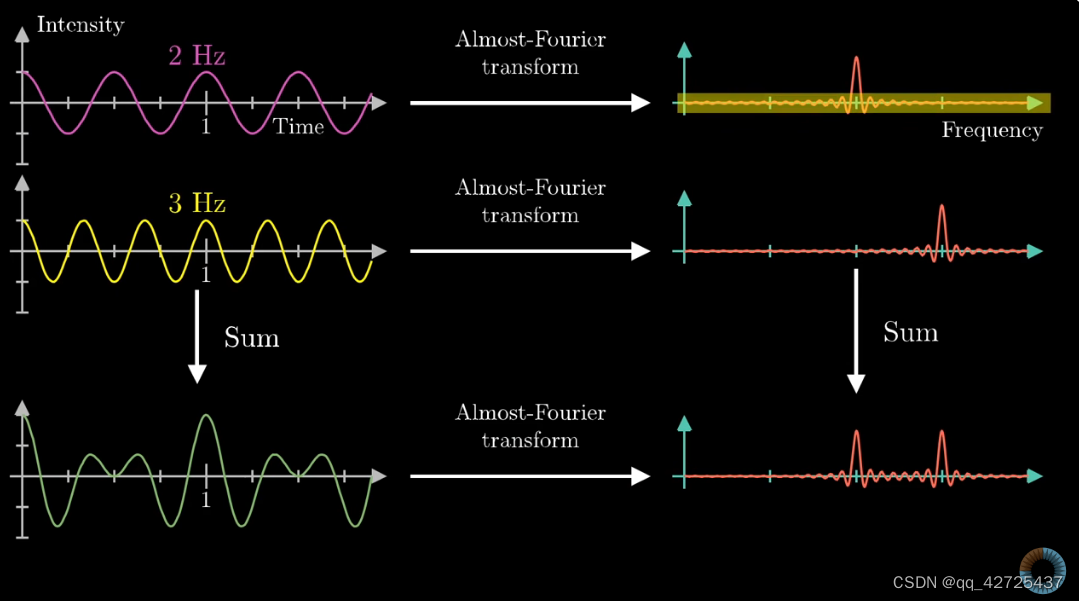
为什么是almost，是因为需要去掉高频信息
反向fourier transform，与正向的没有区别
现在已经有了x轴上的fourier变换，需要考虑y轴，既然是二维，可以用复数域来解决。
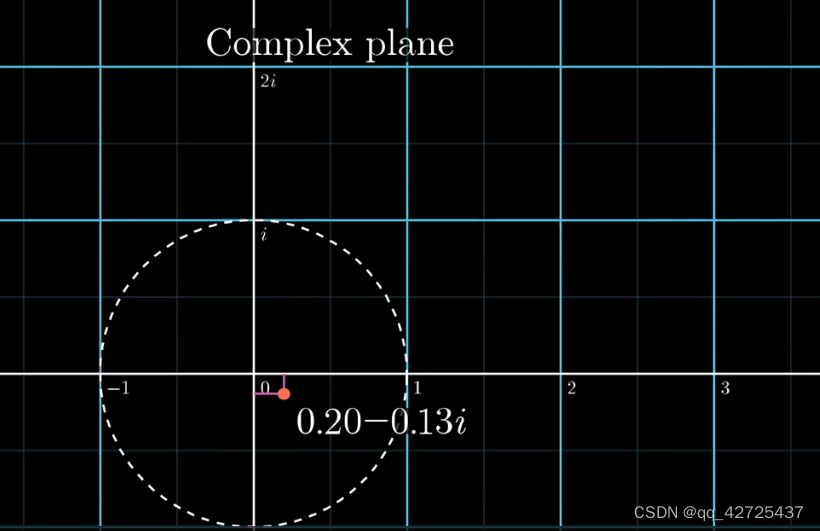
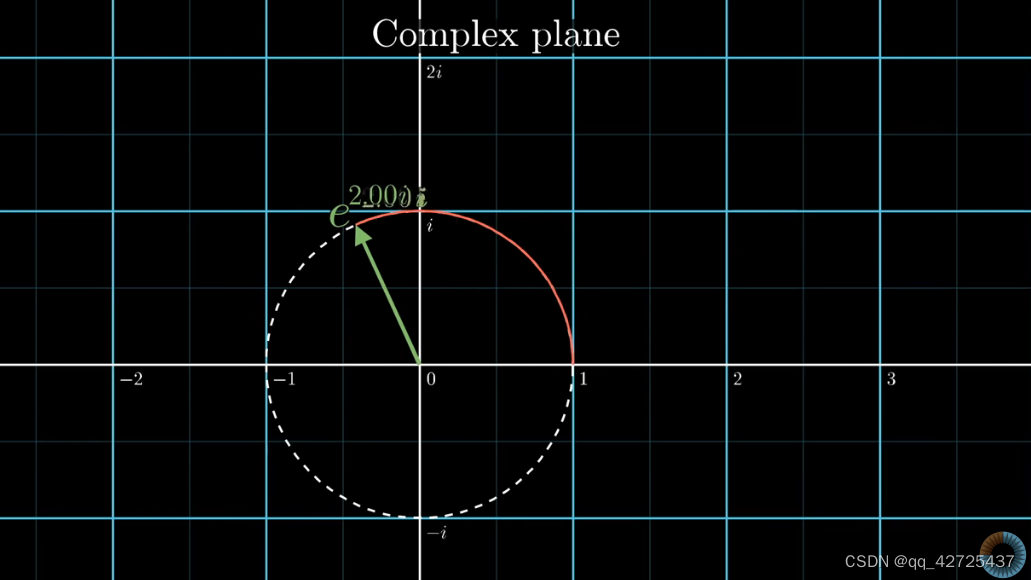
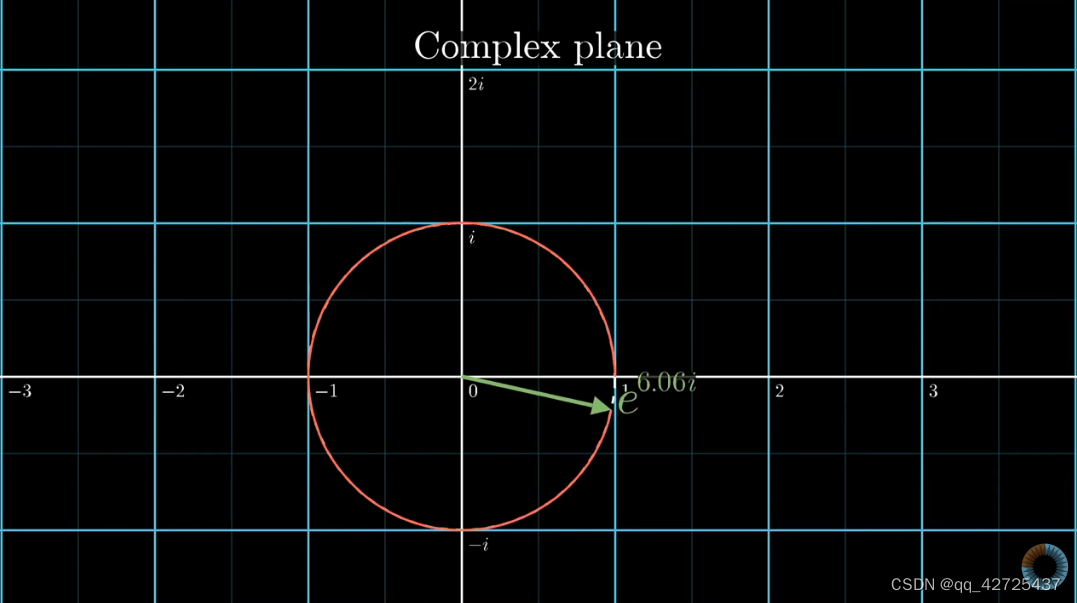
欧拉公式
e
2
π
i
f
t
e^{2\pi ift}
e2πift
其中，f是频率，t是时间，逆时针旋转，那么顺时针旋转
e
?
2
π
i
f
t
e^{-2\pi ift}
e?2πift
再乘以强度g（t），这就是我们需要的
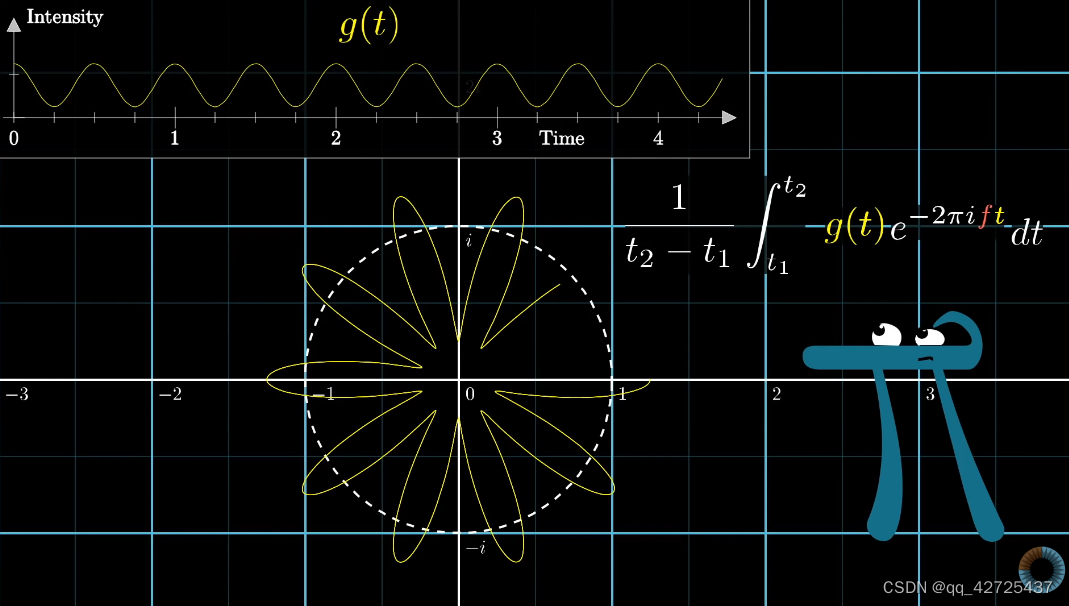
这样就得到了fourier变换公式，但多了
1
t
2
?
t
1
\frac{1}{t_2-t_1}
t2??t1?1?,去掉这一部分就可以表示随着时间变化，质心与原点距离是变化的，不是一成不变的。
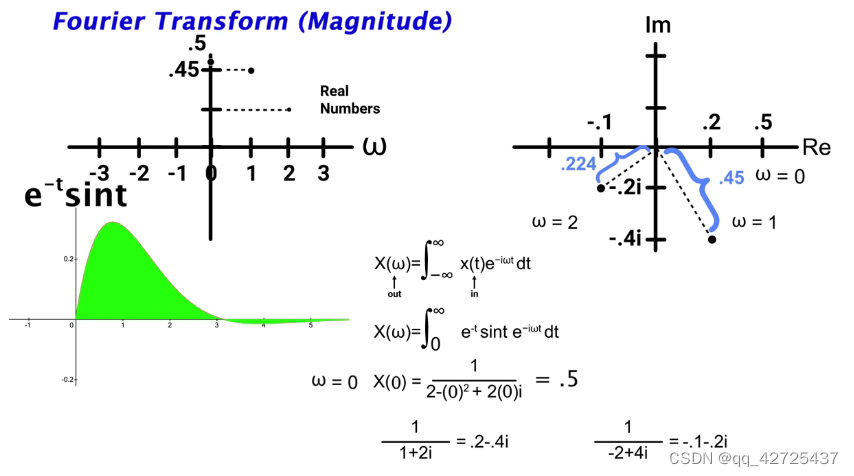
laplace transform
laplace变换就是对
e
?
t
s
i
n
t
e^{-t}sint
e?tsint的fourier变换
X
(
ω
)
=
∫
?
∞
∞
x
(
t
)
e
?
i
ω
t
d
t
X
(
ω
)
=
∫
0
∞
e
?
t
s
i
n
t
e
?
i
ω
t
d
t
X
(
ω
)
=
1
1
+
(
1
+
i
ω
)
2
X
(
ω
)
=
1
2
?
ω
2
+
2
ω
i
X(\omega) = \int^{\infty}_{-\infty}x(t)e^{-i\omega t}dt \\ X(\omega) = \int^{\infty}_{0}e^{-t}sinte^{-i\omega t} dt \\ X(\omega) = \frac{1}{1+(1+i\omega)^2} \\ X(\omega) = \frac{1}{2-\omega^2 + 2\omega i}
X(ω)=∫?∞∞?x(t)e?iωtdtX(ω)=∫0∞?e?tsinte?iωtdtX(ω)=1+(1+iω)21?X(ω)=2?ω2+2ωi1?
从第二个式子到第三个式子的推导如下
X
(
ω
)
=
∫
0
∞
e
?
t
s
i
n
t
e
?
i
ω
t
d
t
=
?
1
1
+
i
ω
∫
0
∞
s
i
n
t
e
?
(
1
+
i
ω
)
t
d
(
?
(
1
+
i
ω
)
t
)
=
?
1
1
+
i
ω
s
i
n
t
e
?
(
1
+
i
ω
)
t
∣
0
∞
+
?
1
1
+
i
ω
∫
0
∞
s
i
n
t
e
?
(
1
+
i
ω
)
t
d
t
=
?
1
1
+
i
ω
∫
0
∞
s
i
n
t
e
?
(
1
+
i
ω
)
t
d
t
=
?
1
(
1
+
i
ω
)
2
c
o
s
t
e
?
(
1
+
i
ω
)
t
∣
0
∞
?
?
1
(
1
+
i
ω
)
2
∫
0
∞
s
i
n
t
e
?
(
1
+
i
ω
)
t
d
t
=
1
(
1
+
i
ω
)
2
?
?
1
(
1
+
i
ω
)
2
∫
0
∞
s
i
n
t
e
?
(
1
+
i
ω
)
t
d
t
\begin{align} X(\omega) &= \int^{\infty}_{0}e^{-t}sinte^{-i\omega t}dt \nonumber \\ &= -\frac{1}{1+i\omega}\int^{\infty}_{0}sinte^{-(1+i\omega) t}d(-(1+i\omega) t) \nonumber \\ &= -\frac{1}{1+i\omega}sint e^{-(1+i\omega) t} |^{\infty}_{0}+ -\frac{1}{1+i\omega}\int^{\infty}_{0}sinte^{-(1+i\omega) t}dt \nonumber \\ &= -\frac{1}{1+i\omega}\int^{\infty}_{0}sinte^{-(1+i\omega) t}dt \nonumber \\ &= -\frac{1}{(1+i\omega)^2}cost e^{-(1+i\omega) t} |^{\infty}_{0} - -\frac{1}{(1+i\omega)^2}\int^{\infty}_{0}sinte^{-(1+i\omega) t}dt\nonumber \\ &= \frac{1}{(1+i\omega)^2}- -\frac{1}{(1+i\omega)^2}\int^{\infty}_{0}sinte^{-(1+i\omega) t}dt\nonumber \\ \end{align}
X(ω)?=∫0∞?e?tsinte?iωtdt=?1+iω1?∫0∞?sinte?(1+iω)td(?(1+iω)t)=?1+iω1?sinte?(1+iω)t∣0∞?+?1+iω1?∫0∞?sinte?(1+iω)tdt=?1+iω1?∫0∞?sinte?(1+iω)tdt=?(1+iω)21?coste?(1+iω)t∣0∞???(1+iω)21?∫0∞?sinte?(1+iω)tdt=(1+iω)21???(1+iω)21?∫0∞?sinte?(1+iω)tdt??
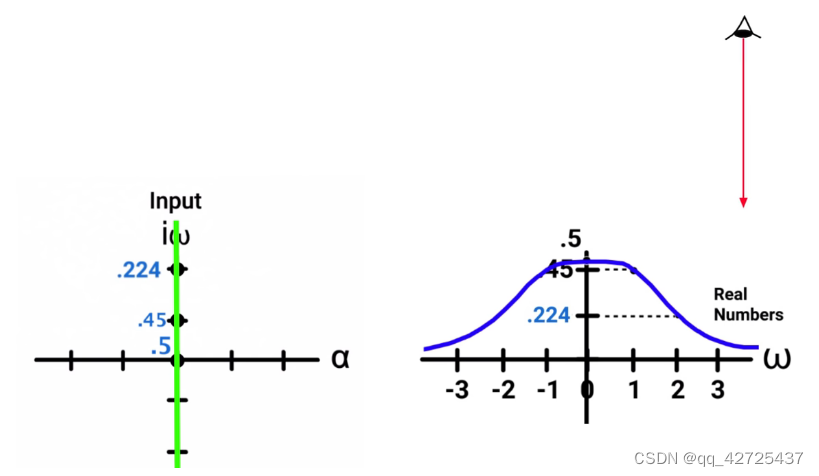
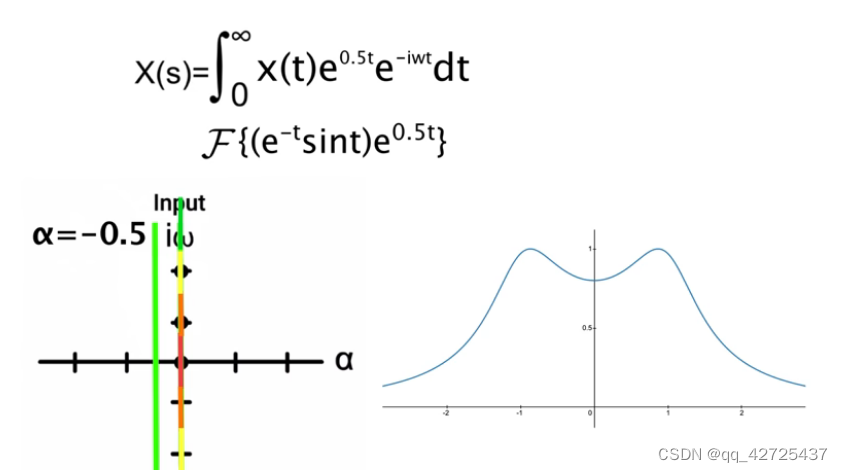
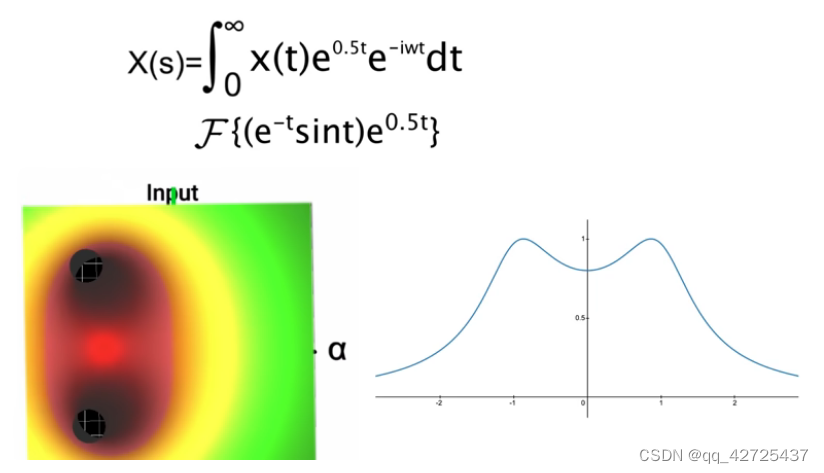
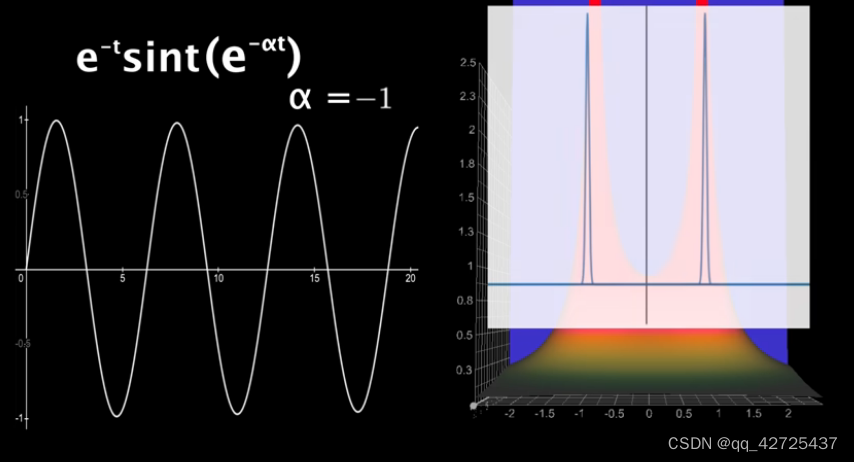
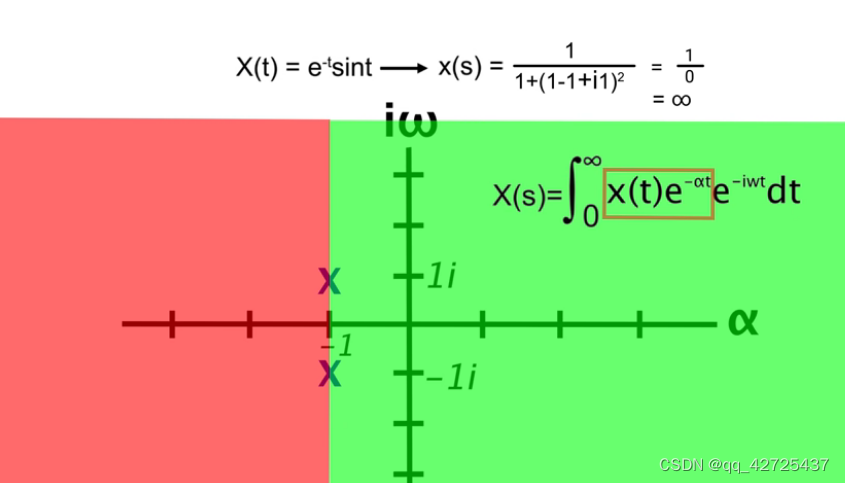
很明显，
ω
\omega
ω控制正弦频率，
α
\alpha
α控制指数衰减
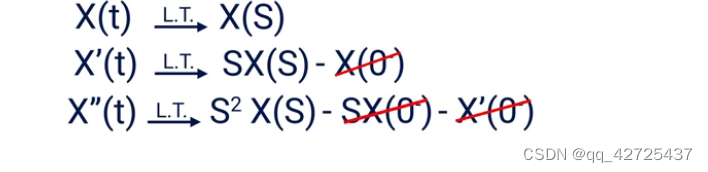
证明如下：
∫
0
∞
x
′
(
t
)
e
?
s
t
d
t
=
x
(
t
)
e
?
s
t
∣
0
∞
+
s
∫
0
∞
e
?
s
t
x
(
t
)
d
t
=
s
x
(
s
)
?
x
(
0
)
\begin{align} \int^{\infty}_{0}x'(t)e^{-st}dt&=x(t)e^{-st}|^{\infty}_{0} + s\int^{\infty}_{0}e^{-st}x(t)dt \nonumber \\ &= sx(s)-x(0) \nonumber \end{align}
∫0∞?x′(t)e?stdt?=x(t)e?st∣0∞?+s∫0∞?e?stx(t)dt=sx(s)?x(0)?
所以laplace变换可以用来求解常微分方程（ODEs）
FFT(快速傅里叶变换)
FFT是DFT的计算方法，首先了解DFT
DFT（离散傅里叶变换）
实际上就是将积分表示为离散的加和形式
X
[
k
]
=
∑
n
=
0
N
?
1
x
n
?
e
?
i
2
π
N
k
n
X[k] = \sum^{N-1}_{n=0}x_n\cdot e^{\frac{-i2\pi}{N}kn}
X[k]=n=0∑N?1?xn??eN?i2π?kn
其中，k是频率，总共有N个采样节点，n代表第n个点。
表示为矩阵形式就是：
[
X
0
,
X
1
,
X
2
,
?
?
,
X
N
?
1
]
?
1
×
N
=
[
x
0
,
x
1
,
x
2
,
?
?
,
x
N
?
1
]
?
1
×
N
[
k
=
0
k
=
1
k
=
2
?
k
=
N
?
1
↓
↓
↓
↓
]
?
N
×
N
\overbrace{[X_0, X_1, X_2, \cdots, X_{N-1}]}^{1\times N} = \overbrace{[x_0, x_1, x_2, \cdots, x_{N-1}]}^{1\times N} \overbrace{\begin{bmatrix} k=0 & k=1 & k=2 & \cdots & k=N-1\\ \Bigg\downarrow & \Bigg\downarrow & \Bigg\downarrow & & \Bigg\downarrow \end{bmatrix}}^{N \times N}
[X0?,X1?,X2?,?,XN?1?]
?1×N?=[x0?,x1?,x2?,?,xN?1?]
?1×N?
?k=0↓
???k=1↓
???k=2↓
?????k=N?1↓
???
?
?N×N?
如果N很小的时候，这个矩阵乘法是容易计算的，但是现实中，对于信号常常有成百上千的采样点，那么计算量就非常大了，所以就需要FFT。
举例：有8个采样点，用不同频率的正弦函数去得到对应频率的值，每一个值是一个bin
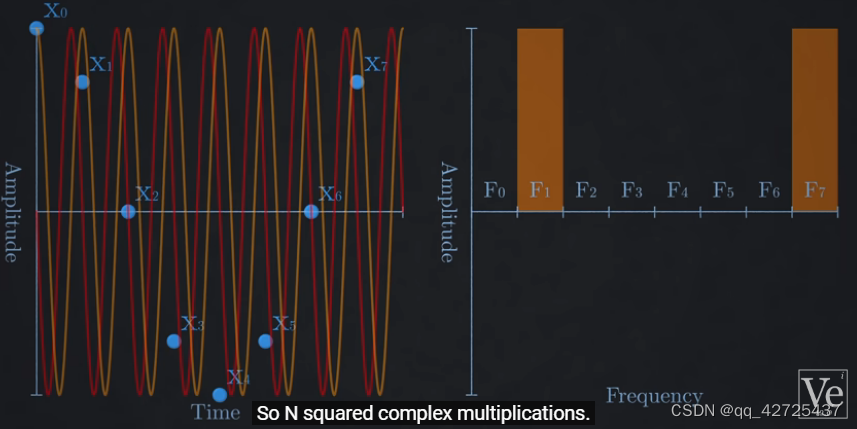
下面需要理解DFT为什么这么做，以及它面临的一些问题
采样频率
首先，根据nyquist定理，要采样频率为f的信号，需要2f+1的采样点，人耳能听到的最高频声音是20khz，所以现实中采样率一般为44.1khz
理想情况
假设有一个f=2hz的余弦，那么我就希望在频域中2的位置有峰值，其他位置为0
那就将离散化得到的向量与不同频率下的波形去求相似性，如果相似度高，就代表该频率下有峰值，这也就是为什么DFT是有效的，意味着采样率一定等于最大频率（N=N）。
但是，通过计算不同频率的波的相似性，会发现问题，
a
1
?
=
a
7
?
\vec{a_1}=\vec{a_7}
a1??=a7??,
a
2
?
=
a
6
?
\vec{a_2}=\vec{a_6}
a2??=a6??等，导致右下图中很多值不为0
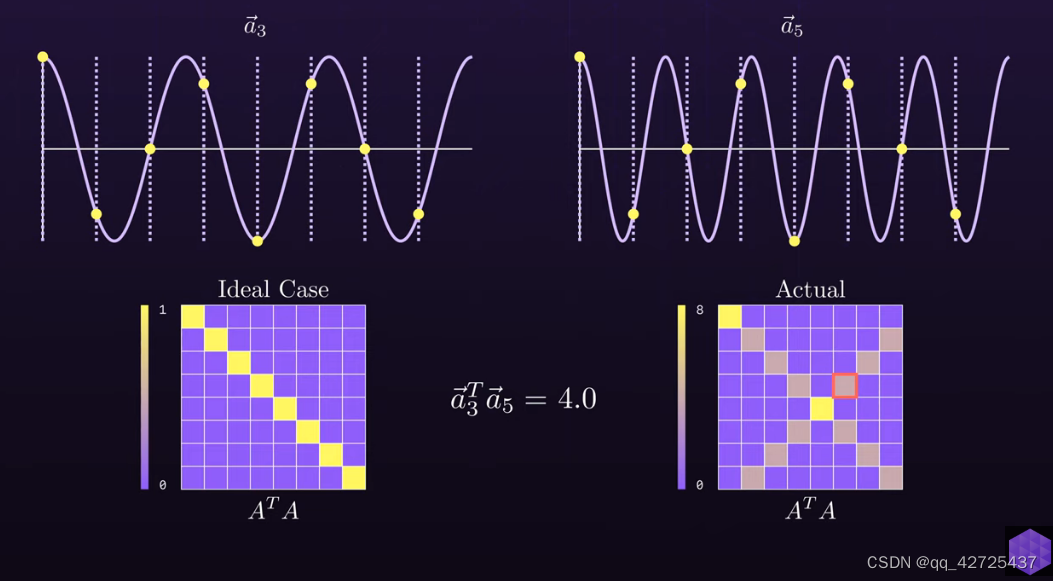
也就是A矩阵不仅不正交，还不可逆，所以不是DFT的最终版本
但是可以发现右下图的左上角这一部分是可逆的，所以每次都采样双倍，但只是采用其中的前半部分。
解决相的问题
通过之前的解决方案，无论是改变幅度，还是频率，或者是初始值，都可以实现FT的功能，但是，当改变相位的时候，频域中的值受到影响，这是不正确的。这是因为在这个变化过程中，无论是sin还是cos都会存在为0的情况，所以要将两者组合在一起。
真正的DFT
就是为sin和cos分别保存一个矩阵，合并后，就得到了我们开始的时候DFT的公式。
FFT引入原因
利用避免重复计算来提升计算速度，上图需要进行64个复数域乘法，改进后，只需要计算24个
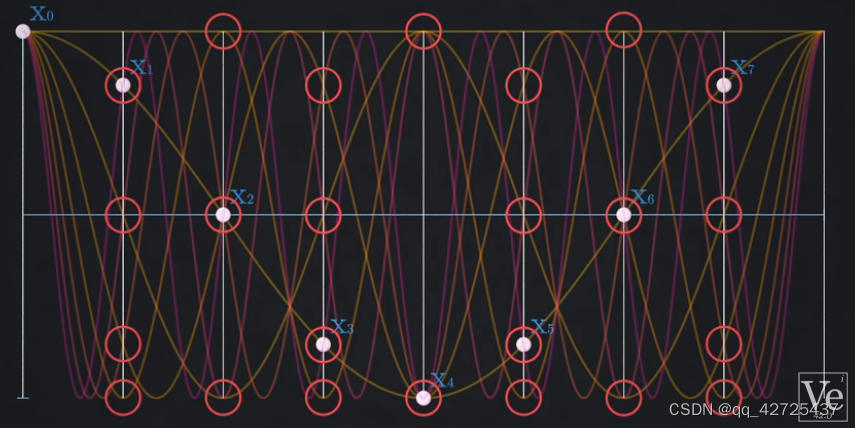
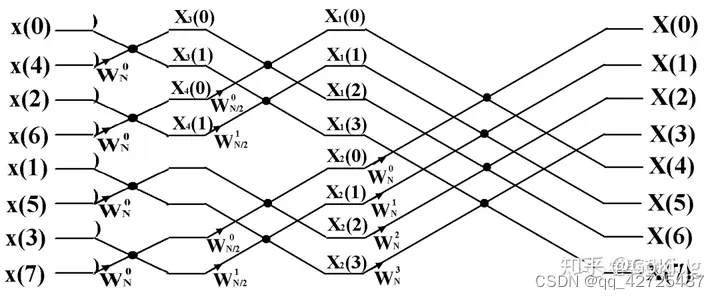
FFT原理
对DFT中的部分用W表示，方便表达
简单来讲就是数学家利用上面提到的旋转因子W的周期性，对称性等性质进行公式化简。在算法编程中则是不断利用已经计算过的点来算新的点，即：旧点算新点。
FFT需要依赖蝶形图进行计算
X
(
k
)
=
∑
n
=
0
N
?
1
x
(
n
)
W
N
n
k
=
∑
n
=
0
,
2
,
4
,
?
N
?
1
x
(
n
)
W
N
n
k
+
∑
n
=
1
,
3
,
5
?
N
?
1
x
(
n
)
W
N
n
k
→
令n=2r
=
∑
r
=
0
,
1
,
?
N
2
?
1
x
(
2
r
)
W
N
2
r
k
+
∑
r
=
0
,
1
,
?
N
2
?
1
x
(
2
r
+
1
)
W
N
(
2
r
+
1
)
k
→
x
(
2
r
)
=
x
1
(
r
)
=
∑
r
=
0
,
1
,
?
N
2
?
1
x
1
(
r
)
W
N
2
r
k
+
∑
r
=
0
,
1
,
?
N
2
?
1
x
2
(
r
)
W
N
(
2
r
+
1
)
k
→
W
N
(
2
r
+
1
)
k
=
W
N
k
?
W
N
/
2
r
k
W
N
2
r
k
=
W
N
/
2
r
k
=
∑
r
=
0
,
1
,
?
N
2
?
1
x
1
(
r
)
W
N
/
2
r
k
+
W
N
k
∑
r
=
0
,
1
,
?
N
2
?
1
x
2
(
r
)
W
N
/
2
(
r
k
)
=
X
1
(
k
)
+
W
N
k
X
2
(
k
)
\begin{align} X(k) &= \sum^{N-1}_{n=0}x(n)W_N^{nk} \nonumber \\ &= \sum^{N-1}_{n=0,2,4,\cdots}x(n)W_N^{nk} + \sum^{N-1}_{n=1, 3, 5\cdots}x(n)W_N^{nk} \xrightarrow{\text{令n=2r}}\nonumber \\ &= \sum^{\frac{N}{2}-1}_{r=0,1,\cdots}x(2r)W_N^{2rk} + \sum^{\frac{N}{2}-1}_{r=0,1, \cdots}x(2r+1)W_N^{(2r+1)k} \xrightarrow{x(2r)=x_1(r)}\nonumber \\ &= \sum^{\frac{N}{2}-1}_{r=0,1,\cdots}x_1(r)W_N^{2rk} + \sum^{\frac{N}{2}-1}_{r=0,1, \cdots}x_2(r)W_N^{(2r+1)k} \xrightarrow[W_N^{(2r+1)k} = W_{N}^{k} * W_{N/2}^{rk}]{W_N^{2rk}=W_{N/2}^{rk}}\nonumber \\ &= \sum^{\frac{N}{2}-1}_{r=0,1,\cdots}x_1(r)W_{N/2}^{rk} + W_N^k\sum^{\frac{N}{2}-1}_{r=0,1, \cdots}x_2(r)W_{N/2}^{(rk)} \nonumber \\ &=X_1(k)+W_N^kX_2(k) \nonumber \end{align}
X(k)?=n=0∑N?1?x(n)WNnk?=n=0,2,4,?∑N?1?x(n)WNnk?+n=1,3,5?∑N?1?x(n)WNnk?令n=2r?=r=0,1,?∑2N??1?x(2r)WN2rk?+r=0,1,?∑2N??1?x(2r+1)WN(2r+1)k?x(2r)=x1?(r)?=r=0,1,?∑2N??1?x1?(r)WN2rk?+r=0,1,?∑2N??1?x2?(r)WN(2r+1)k?WN2rk?=WN/2rk?WN(2r+1)k?=WNk??WN/2rk??=r=0,1,?∑2N??1?x1?(r)WN/2rk?+WNk?r=0,1,?∑2N??1?x2?(r)WN/2(rk)?=X1?(k)+WNk?X2?(k)?
上面的过程没有减少运算量继续进行简化
∵
X
(
k
)
=
∑
r
=
0
,
1
,
?
N
2
?
1
x
1
(
r
)
W
N
/
2
r
k
∴
X
1
(
k
+
N
/
2
)
=
∑
r
=
0
,
1
,
?
N
2
?
1
x
1
(
r
)
W
N
/
2
r
(
k
+
N
/
2
)
=
∑
r
=
0
,
1
,
?
N
2
?
1
x
1
(
r
)
W
N
/
2
r
k
=
X
1
(
k
)
\because X_(k) = \sum^{\frac{N}{2}-1}_{r=0,1,\cdots}x_1(r)W_{N/2}^{rk} \\ \therefore X_1(k+N/2) = \sum^{\frac{N}{2}-1}_{r=0,1,\cdots}x_1(r)W_{N/2}^{r(k+N/2)}=\sum^{\frac{N}{2}-1}_{r=0,1,\cdots}x_1(r)W_{N/2}^{rk} = X_1(k)
∵X(?k)=r=0,1,?∑2N??1?x1?(r)WN/2rk?∴X1?(k+N/2)=r=0,1,?∑2N??1?x1?(r)WN/2r(k+N/2)?=r=0,1,?∑2N??1?x1?(r)WN/2rk?=X1?(k)
同理，
X
2
(
k
+
N
/
2
)
=
X
2
(
k
)
X_2(k+N/2) = X_2(k)
X2?(k+N/2)=X2?(k)
∵
X
(
k
)
=
X
1
(
k
)
+
W
N
k
X
2
(
k
)
∴
X
(
k
+
N
/
2
)
=
X
1
(
k
+
N
/
2
)
+
W
N
k
+
N
/
2
X
2
(
k
+
N
/
2
)
→
W
N
k
+
N
/
2
=
?
W
N
k
=
X
1
(
k
+
N
/
2
)
+
W
N
k
X
2
(
k
+
N
/
2
)
=
X
1
(
k
)
?
W
N
k
X
2
(
k
)
\because X(k)=X_1(k)+W_N^kX_2(k) \\ \therefore \begin{align} X(k+N/2)&=X_1(k+N/2)+W_N^{k+N/2}X_2(k+N/2) \xrightarrow{W_N^{k+N/2}=-W_N^k} \nonumber \\ &= X_1(k+N/2)+W_N^{k}X_2(k+N/2) = X_1(k)-W_N^kX_2(k) \nonumber \end{align}
∵X(k)=X1?(k)+WNk?X2?(k)∴X(k+N/2)?=X1?(k+N/2)+WNk+N/2?X2?(k+N/2)WNk+N/2?=?WNk??=X1?(k+N/2)+WNk?X2?(k+N/2)=X1?(k)?WNk?X2?(k)?
综上推导得到：
X
(
k
)
=
X
1
(
k
)
+
W
N
k
X
2
(
k
)
X
(
k
+
N
/
2
)
=
X
1
(
k
)
?
W
N
k
X
2
(
k
)
X(k)=X_1(k)+W_N^kX_2(k) \\ X(k+N/2) = X_1(k)-W_N^kX_2(k)
X(k)=X1?(k)+WNk?X2?(k)X(k+N/2)=X1?(k)?WNk?X2?(k)
这里都是用X1和X2来计算，所以缩减了计算量
继续推导
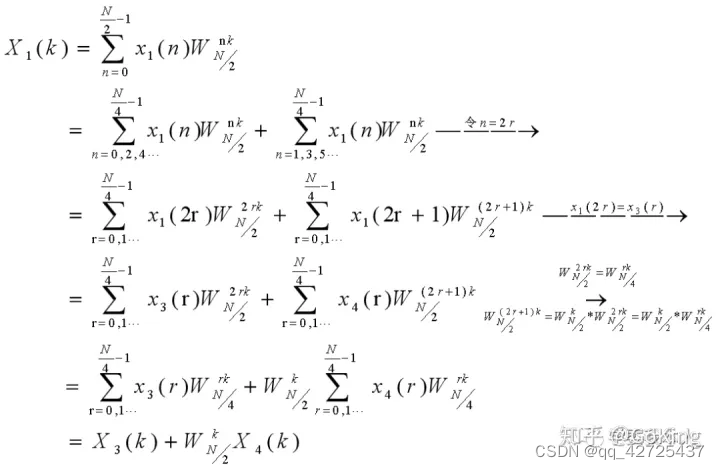
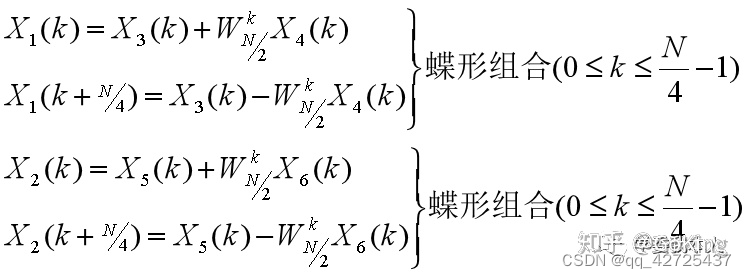
最后一步
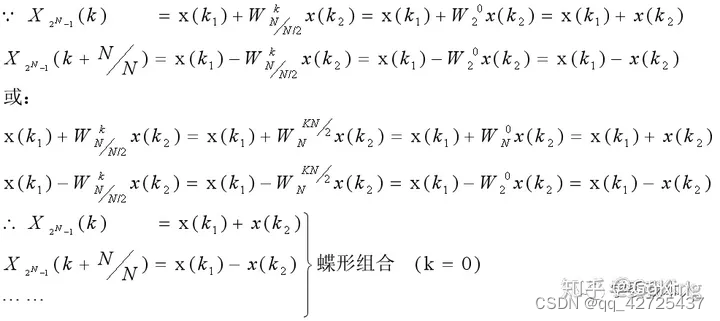
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 谷歌浏览器安装插件提示无法从该网站添加怎么办？
- 安卓恢复指南:五种安卓数据恢复软件推荐
- 【Proteus仿真】【Arduino单片机】路灯控制系统
- 【Mybatis】日常知识点随笔（持续更新）
- 2024，智能座舱不要再过度“装修”了！
- 面试题：为什么数据库连接池不采用 IO 多路复用？
- 5g消息-5G时代短信升级-富媒体智能交互-互联网新入口
- 学习如何使用 Python 连接 MongoDB: PyMongo 安装和基础操作教程
- 时空预测 | 基于图神经网络的时空预测
- Open Babel 命令行使用 + 利用Open Babel将smiles转为image（分子图像）