142.环形链表 II 、141. 环形链表（附带源码）

目录

一、142问题的分析与解决：

二、怎么做？

三、142代码

四、141代码

---

一、142问题的分析与解决：

核心：定义快慢指针：slow、fast

思路是当快指针fast进环时，慢指针slow一定没有进环

这个时候就是就变成了快指针追慢指针的问题。

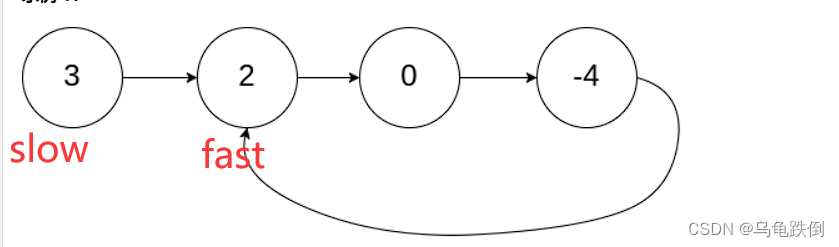
但是会有两种情况：那么当慢指针开始进环，此时快指针fast的状态有以下几种情况：

1、环比较小，fast在里面绕环n次

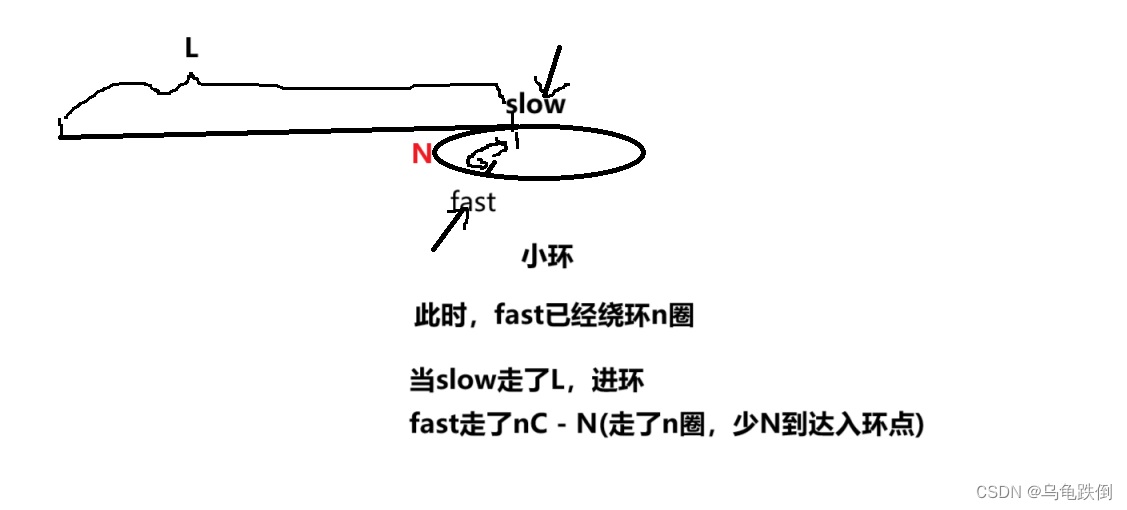
2、环比较大，fast在里面环绕不到一次

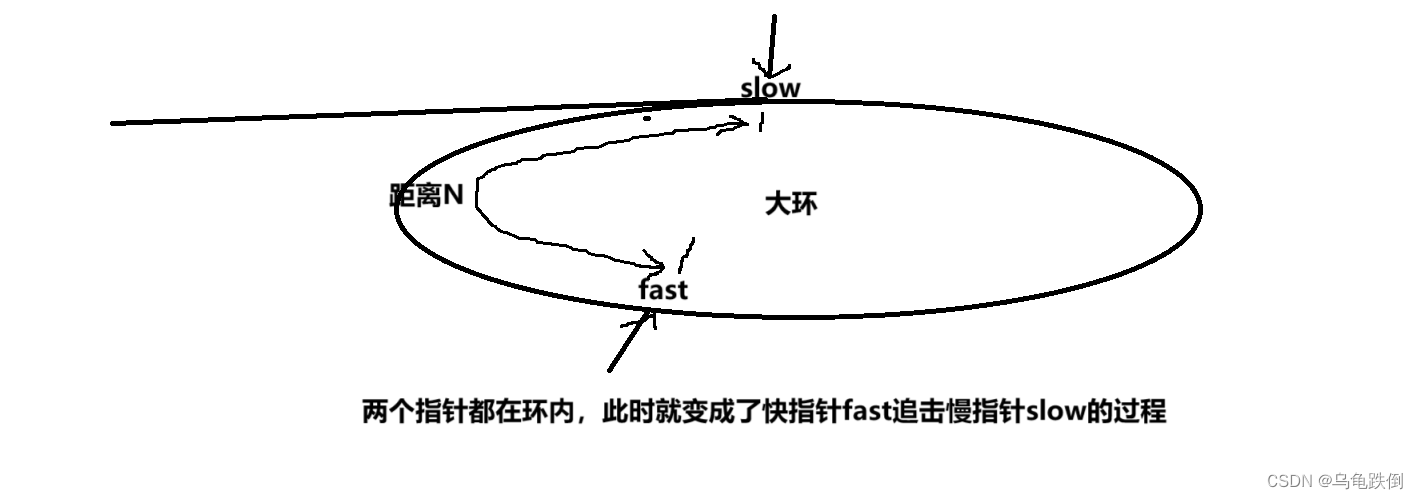
那么怎么解决以上的追击问题呢？
1、快慢指针，慢指针走一步，快指针走两步
2、为什么一定会相遇？假设慢指针进环的时候，快指针和慢指针距离N，则每一次快慢指针的距离会减1
而如果假设慢指针走一步，快指针走三步，每一次快慢指针距离减少2，如果距离是奇数，就会错过；如果是偶数就会相遇(事实上这个是不成立的，有兴趣的同学可以自行证明)

（画图分析）

从出发点到入环点：L

环长：C

相遇点距离如环点：X

slow走的路程：L + X

fast走的路程： L + (n-1)*C? + C - X

slow走一步，fast走两步，他们之间的路程呈现二倍关系,同时，因为fast每一次走两步，所以slow一定不会走超过一圈，如果超过一圈，那么意味着fast走了两圈，但是不可能，因为fast走一圈就一定会追上slow

2(X + L ) =?L + (n-1)*C? + C - X

L=(n-1)C + c-x

推出这个公式有什么意义呢？
意义：两个指针同时间从相遇位置开始走，会在进入环位置相遇

这个公式如何理解？

L是出发点到入环点的距离

(n-1)*C? + C - X是相遇点的位置

一个指针从相遇位置走(n-1)*C+(C - x )
如何理解:走了n-1圈，最后从相遇位置再走C-X到达入环点
而因为我们推出公式:L=(n-1)C + C-x
所以走的这个路程，就等于L!
也就是说，两个指针同时从相遇位置和出发点开始走，会在入环点相遇，因为两者之间到达入环点的距离相等

二、怎么做？

分析到这里，我们就可以解决这个问题了。

首先，通过快慢指针找到相遇点，记录相遇点，

然后，让两个指针，同时从初始位置和相遇位置同时出发，相遇位置就是入环电。

三、142代码

struct ListNode *detectCycle(struct ListNode *head) 
{
struct ListNode *slow ,*fast;
    slow = fast = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast)
        {
            struct ListNode *meet = slow;
            while(meet != head)
            {
                meet = meet->next;
                head = head->next;
            }
          return meet;
          
        }
    }
return NULL;
}

四、141代码

bool hasCycle(struct ListNode *head) {
    

struct ListNode *slow ,*fast;
    slow = fast = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast)
        {
            
          return true;
          
        }
    }
return false;


}