【数据结构】栈的远房亲戚——队列

前言
大家好,很高兴又和大家见面啦!!!
在经过前面内容的介绍,我们已经知道了什么是栈,以及栈的一些基本操作。在介绍完如何通过C语言实现顺序栈之后,我们又详细介绍了顺序栈中的共享栈以及链栈的C语言实现,相信大家现在对栈已经有了一定的理解了。今天我们将来介绍一下栈的一位远房亲戚——队列。在今天的内容中,我们将会介绍以下内容:
- 什么是队列?
- 队列有哪些重要术语?
- 队列有哪些基本操作?
下面我们就来开始今天的内容吧!
一、队列的定义
队列(Queue)简称队,也是一种操作受限的线性表——只允许在表的一端进行插入,而在表的另一端进行删除。
有了栈的知识基础,我们现在就可以很容易的理解什么是操作受限了,如下图所示:

从图中可以看到,队列中存储的元素在逻辑上是以线性结构进行存储,所以队列也是一种线性表,但是数据元素在队列中只能从一端进入队列,另一端离开队列,也就是说,队列中的元素在队列中进行一些基本操作时是受到限制的,并不能像顺序表与链表一样,可以在任意位置进行插入或者删除操作。
二、队列的重要术语
在队列中,如果我们要插入一个元素,那么插入的这个操作我们称为入队或者进队;
在队列中,如果我们要删除一个元素,那么删除的这个操作我们称为出队或者离队;
在队列中,允许进行插入的一端我们将其称为对尾,而允许进行删除的一端我们将其称为队首或者队头;
当一个队列中不含任何元素时我们将其称为空队列,如下图所示:
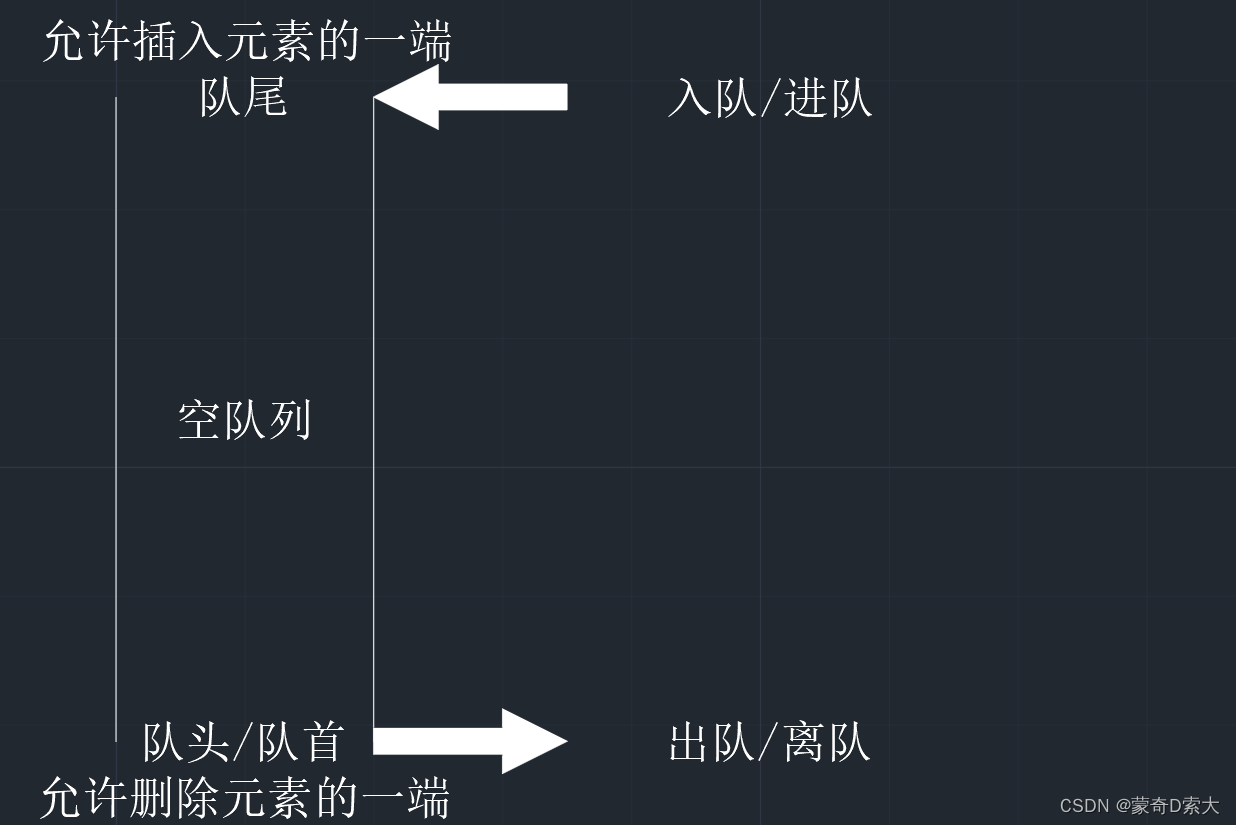
队列的这种限制与我们实际生活中的队列也是一样的,比如我们在买东西时,需要排一条长长的队伍,当有新的人进入这个队伍时,是需要排在队伍的最后面,而排在最前面的人在买完东西后就可以直接离开队伍了。
从上述介绍我们可以知道队列的操作特性是——先进先出(First In First Out, FIFO)。之所以说它是栈的远房亲戚就是因为它们都是操作受限的一类线性表,只不过它们的操作特性是截然相反的:
- 栈 的操作特性——后进先出(Last In First Out, LIFO);
- 队列的操作特性——先进先出(First In First Out, FIFO);
当队列中存储了元素之后,队列中的第一个元素我们将其称为队头元素,队列中的最后一个元素我们将其称为队尾元素。
三、队列的基本操作
队列的基本操作也是离不开我们的口诀——创建销毁、增删改查。在队列中,主要涉及的基本操作如下所示:
InitQueue(&Q):初始化队列,构造一个空队列Q;
QueueEmpty(Q):队列判空,如果队列为空可以返回true,否则返回false;
EnQueue(&Q,x):入队,若队列Q未满,则将x加入队列,使其称为新的队尾;
DeQueue(&Q,&x):出队,若队列Q非空,删除对头元素,并将删除的元素用x带回主函数;
GetHead(Q,&x):读队头元素,若队列Q非空,则将队头元素赋值给x;
DestroyQueue(&Q):销毁队列,销毁并释放队列Q所占的内存空间。
通过C语言来定义这些基本操作的话则是如下所示:
//队列的初始化
void InitQueue(QueueType* Q);
//队列的判空
bool QueueEmpty(QueueType Q);
//队列的入队
void EnQueue(QueueType* Q, ElemType x);
//队列的出队
void DeQueue(QueueType* Q, ElemType* x);
//队列的查找——读取队头元素
void GetHead(QueueType Q, ElemType* x);
//队列的销毁
void DestroyQueue(QueueType* Q);
void test() {
QueueType Q;
InitQueue(&Q);
QueueEmpty(Q);
EnQueue(&Q, x);
DeQueue(&Q, &x);
GetHead(Q, &x);
DestroyQueue(&Q);
}
这些基本操作中除了判空与查找两个操作外,其他的操作都会对队列进行修改,因此我们需要在进行传参时对判空和查找这两个操作进行传值传参,这时我们只是需要队列的一份临时拷贝即可,而对于其他操作我们则需要通过传址的方式完成传参,这样便于对实参进行直接的修改;
而对于入队、出队与查找而言,这里多加了一个变量x,但是根据实际情况的不同于实现方式的不同这里的形参x的传参方式也会略有不同,这里我们在后面的具体实现中会展开介绍。
四、数据结构的三要素
在前面的介绍中,有一个问题一直是我们忽视的,那就是数据结构的三要素——数据的逻辑结构、数据的存储结构以及数据的运算。
在绪论中我们曾介绍过,数据结构的三要素:
- 数据的逻辑结构:指的是数据元素之间的逻辑关系,即从逻辑上来描述数据;
- 数据的存储结构:指的是数据元素在内存中的物理位置关系,即从物理位置上来描述数据;
- 数据的运算:数据的元素包括定义与实现。
- 运算的定义针对的是逻辑结构,即对于不同的逻辑结构的数据我能执行的操作有哪些;
- 而运算的实现针对的是存储结构,即对于不同的存储结构的数据,我应该如何实现这些操作;
在复习完这些内容后,我们再来从三要素的角度来分析线性表、栈以及队列;
4.1 线性表的三要素
在介绍线性表时,我们曾提过一嘴,线性表反映的是数据元素的逻辑结构,而顺序表和链表反映的是数据元素的存储结构,当时我们并未详细展开说明这句话,现在有了这么多知识的积累,我们再回过头来理解这句话就能够有了第一层初步的理解了;
- 线性表指的是数据元素在逻辑上是像一条线段一样,这也就是为什么线性表中的各个元素除了首元素外,其他元素都有且只有一个直接前驱,除了最后一个元素外,其他元素都有且只有一个直接后继,因为一条线段它从头到尾都是笔直的,不会有任何的分叉;
- 顺序表和链表反映的是数据元素在内存中的存储情况——物理位置上相邻的存储方式为顺序存储,物理位置上不相邻的方式为链式存储。
- 因此即满足物理位置上相邻又满足逻辑上相邻的线性表我们称为顺序表;
- 满足逻辑上相邻但是物理位置上不相邻的线性表我们称为链表;
- 对与线性表这种逻辑结构而言,我们对其定义的基本操作就是可以进行按值查找与按位查找两种查找方式,因此,我们可以对线性表进行任意结点的增加与删除操作;
- 而在是实现这些操作时,由于它们的存储结构,我们对顺序表进行遍历时可以直接通过下标进行遍历,而对于链表而言我们则需要通过指针域来进行遍历;
4.2 栈的三要素
在介绍栈时,我们首先介绍的是栈是一种操作受限的线性表,它只允许从栈顶进行增加与删除操作,具体为什么会这样,我们前面并没有详细说明,现在我们来看一下栈的三要素分别是什么:
- 栈反映的是数据元素的逻辑关系,在栈中的元素在逻辑上也是呈现线性关系的,即栈中的元素在逻辑上除了首元素外,其他元素都有且只有一个直接前驱,除了尾元素外,其他元素都有且只有一个直接后继;
- 栈中的元素在存储时如果是通过顺序存储的方式则栈中的元素满足逻辑上相邻且物理位置上也相邻;如果是通过链式存储的方式则栈中的元素满足逻辑上相邻,但是物理位置上不一定相邻;也就是说顺序栈与链栈是反映的栈中的数据元素在内存空间中的物理位置关系;
- 对于栈这种逻辑结构,我们规定了元素只能从栈顶入栈和出栈,并且在访问栈中的元素时只能访问栈顶元素;
- 而对于他的存储结构而言,我们在实现对应操作时,顺序栈和共享栈因为栈中的各个元素在物理位置上是相邻的,所以我们可以直接通过下标来实现对应操作;在链栈中因为各个元素在物理位置上不一定相邻,所以我们则是通过指针来实现对应的操作;
4.3 队列的三要素
对于队列而言,我们同样也是说它是一种操作受限的线性表,这里有两个关键信息——操作受限、线性表,这里反映的分别是数据元素的运算以及数据元素的逻辑结构,下面我们也来解剖一下队列:
- 队列反映的是数据元素的逻辑结构,从它的定义中我们可以知道,队列这种逻辑结构实际上也是线性结构,数据元素在逻辑上是线性连接的,即除了首元素外其他元素有且只有一个直接前驱,除了尾元素外其他元素有且只有一个直接后继;
- 队列中的数据元素在内存中存储时同样也是有顺序存储与链式存储两种方式,在之后的篇章中我们会详细介绍队列的不同存储结构;
- 从队列的操作受限我们可以得知,队列中的数据在进行运算时和栈一样,一些基本操作同样也是受到限制的,只不过我们规定的是在队列中,元素只允许从队尾进入队列,元素也只允许从队头离开队列,并且我们能访问的也只有队头元素,并不能随意读取队列中间的某个元素;
- 队列这些操作的具体实现在不同的存储结构中也是略有差异的,具体的实现过程我们会在后续的篇章中详细介绍;
结语
在剖析完了线性表、栈以及队列的三要素,我相信大家对于这三种数据结构应该有了进一步的理解,接下来随着学习的深入,我们也会更加深层次的探讨并理解这些知识点,希望大家能够跟随博主一直坚持下去。
今天的内容到这里就全部介绍完了,希望今天的内容能够给大家对队列这种新的数据结构留下一个初步的认知,并且能够帮助大家进一步理解线性表与栈这两种数据结构。在接下来的内容中,我们将会详细介绍如何通过C语言来实现队列,大家记得关注哦!
最后感谢各位的翻阅,咱们下一篇内容见!!!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- spring boot 集成邮件发送功能
- 你好,2024!再见,2023!
- Safari浏览器css兼容文本超出处理
- MATLAB Mobile - 使用预训练网络对手机拍摄的图像进行分类
- 后台管理系统html页面模板推荐
- 双侧电源系统距离保护MATLAB仿真模型
- 25,verilog之generate生成块
- Mysql从入门到精通
- 机器学习笔记 - 基于OpenCV+稀疏光流的无监督运动检测
- 12.21 汇编点亮STM32MP157小灯