【图的应用一：最小生成树】- 用 C 语言实现普里姆算法和克鲁斯卡尔算法

发布时间：2023年12月18日

一、最小生成树?

假设要在 n 个城市之间建立通信联络网，则连通 n 个城市只需要 n - 1 条线路。这时，自然会考虑这样一个问题，如何在最节省经费的前提下建立这个通信网。

在每两个城市之间都可设置一条线路，相应地都要付出一定的经济代价。n 个城市之间，最多可能设置 ? $C_n^2 = \dfrac{n(n - 1)}{2}$ ?条线路，那么如何在这些可能的线路中选择 n - 1 条，以使总的耗费最少呢？

可以用连通网来表示 n 个城市，以及 n 个城市间可能设置的通信路线，其中网的顶点表示城市，边表示两城市之间的线路，赋予边的权值表示相应的代价。对于 n 个顶点的连通网可以建立许多不同的生成树，每一颗生成树都可以是一个通信网，最合理的通信网应该是各边代价之和最小的那颗生成树，称为连通网的最小代价生成树（Minimum Cost Spanning Tree），简称最小生成树。

构造最小生成树有多种算法，其中多数算法利用了最小生成树的下列一种简称为 MST 的性质：

假设 N = (V, E) 是一个连通网，U 是顶点集 V 的一个非空真子集。若 (u, v) 是 N 中所有的一个顶点在 U（ $u \in U$ ?）中，另一个顶点在 V - U（? $v \in V - U$ ）中的边里，具有最小权值的一条边，则必存在一棵包含边 (u, v) 的最小生成树。

可以用反证法来证明：

假设网 N 的任何一棵最小生成树都不包含边 (u, v)，T 是连通网上的一棵最小生成树，由生成树的定义可知，T 中必存在一条从 u 到 v 的路径 P，且在 P 上必存在一条边 (u', v')，其中 $u' \in U, v' \in V - U$ ?。

当将边 (u, v) 加入到 T 中时，(u, v) 和 P 构成了一条回路，删去 (u', v') 便可消除回路，同时得到另一颗生成树 T‘。因为 (u, v) 的权值不高于 (u', v')，所以 T' 的权值亦不高于 T，那么 T’ 是包含 (u, v) 的一棵最小生成树，和假设矛盾。

普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法是两个利用 MST 性质构造最小生成树的算法。

二、普里姆算法的构造过程

假设 N = (V, E) 是连通网，TE 是 N 上最小生成树中边的集合。

$U = \{u_0\}(u_0 \in V), TE = \{\}$ ?。
在所有 ? $u \in U, v \in V - U$ ?的边? $(u, v) \in E$ ?中找一条权值最小的边? $(u_0, v_0)$ ?并入集合 TE，同时 ? $v_0$ ?并入 U。
重复 2，直至 U = V 为止。

此时 TE 中必有 n - 1 条边，则 T = (V, TE) 为 N 的最小生成树。

下图所示为一个连通网 G5 从 v1 开始构造最小生成树的例子。可以看出，普里姆算法逐步增加 U 中的顶点，可称为 "加点法"。

每次选择最小边时，可能存在多条同样权值的边可选，此时任选其一即可。

三、普里姆算法的实现

假设无向网 N 以邻接矩阵形式存储，从顶点 u 出发构造 N 的最小生成树 T，要求输出 T 的各条边。

为实现这个算法附设了两个辅助数组 lowcostArr 和 adjVexPosArr。对每个顶点，lowcostArr[i - 1] = Min{ cost? }，即表示 N 中所有的一个顶点在 U 中，另一个顶点是 vi 的边里，最小边上的权值；adjVexPosArr[i - 1] 则表示那条最小边在 U 中的那个顶点在图中的位置。

AMGraph.h：

#pragma once
?
// 无向网
typedef char VertexType;
typedef int EdgeType;
?
#define DEFAULT_CAPACITY 2
?
typedef struct AMGraph
{
    VertexType* vertices;
    EdgeType** edges;
    int vSize;
    int eSize;
    int capacity;
}AMGraph;
?
// 基本操作
void AMGraphInit(AMGraph* pg);
?
void ShowAdjMatrix(AMGraph* pg);
?
int GetVertexPos(AMGraph* pg, VertexType v);
?
void InsertVertex(AMGraph* pg, VertexType v);
void InsertEdge(AMGraph* pg, VertexType v1, VertexType v2, EdgeType cost);
?
// 普里姆算法
void MiniSpanTree_Prim(AMGraph* pg, VertexType u);

AMGraph.c：

#include "AMGraph.h"
#include <assert.h>
#include <stdlib.h>
#include <stdio.h>
?
void AMGraphInit(AMGraph* pg)
{
    assert(pg);
    pg->vSize = pg->eSize = 0;
    pg->capacity = DEFAULT_CAPACITY;
    
    pg->vertices = (VertexType*)malloc(sizeof(VertexType) * pg->capacity);
    assert(pg->vertices);
?
    pg->edges = (EdgeType**)malloc(sizeof(EdgeType*) * pg->capacity);
    assert(pg->edges);
    for (int i = 0; i < pg->capacity; ++i)
    {
        pg->edges[i] = (EdgeType*)malloc(sizeof(EdgeType) * pg->capacity);
        assert(pg->edges[i]);
        for (int j = 0; j < pg->capacity; ++j)
        {
            if (i == j)
                 ?pg->edges[i][j] = 0;
            else
                 ?pg->edges[i][j] = INT_MAX;
        }
    }
}
?
void ShowAdjMatrix(AMGraph* pg)
{
    assert(pg);
    printf("  ");
    for (int i = 0; i < pg->vSize; ++i)
    {
        printf("%c ", pg->vertices[i]);
    }
    printf("\n");
?
    for (int i = 0; i < pg->vSize; ++i)
    {
        printf("%c ", pg->vertices[i]);
        for (int j = 0; j < pg->vSize; ++j)
        {
            if (pg->edges[i][j] == INT_MAX)
                printf("# "); ?// 用 # 代替 ∞
            else
                printf("%d ", pg->edges[i][j]);
        }
        printf("\n");
    }
}
?
int GetVertexPos(AMGraph* pg, VertexType v)
{
    assert(pg);
    for (int i = 0; i < pg->vSize; ++i)
    {
        if (pg->vertices[i] == v)
            return i;
    }
    return -1;
}
?
void InsertVertex(AMGraph* pg, VertexType v)
{
    assert(pg);
    // 考虑是否需要扩容
    if (pg->vSize == pg->capacity)
    {
        VertexType* tmp1 = (VertexType*)realloc(pg->vertices, sizeof(VertexType) * 2 * pg->capacity);
        assert(tmp1);
        pg->vertices = tmp1;
?
        EdgeType** tmp2 = (EdgeType**)realloc(pg->edges, sizeof(EdgeType*) * 2 * pg->capacity);
        assert(tmp2);
        pg->edges = tmp2;
        for (int i = 0; i < pg->capacity; ++i)
        {
            EdgeType* tmp3 = (EdgeType*)realloc(pg->edges[i], sizeof(EdgeType) * 2 * pg->capacity);
            assert(tmp3);
            pg->edges[i] = tmp3;
            for (int j = pg->capacity; j < 2 * pg->capacity; ++j)
            {
                pg->edges[i][j] = INT_MAX; ?
            }
        }
        for (int i = pg->capacity; i < 2 * pg->capacity; ++i)
        {
            pg->edges[i] = (EdgeType*)malloc(sizeof(EdgeType) * 2 * pg->capacity);
            assert(pg->edges[i]);
            for (int j = 0; j < 2 * pg->capacity; ++j)
            {
                if (i == j)
                    pg->edges[i][j] = 0;
                else
                    pg->edges[i][j] = INT_MAX;
            }
        }
?
        pg->capacity *= 2;
    }
    // 插入顶点
    pg->vertices[pg->vSize++] = v;
}
?
void InsertEdge(AMGraph* pg, VertexType v1, VertexType v2, EdgeType cost)
{
    assert(pg);
    int pos1 = GetVertexPos(pg, v1);
    int pos2 = GetVertexPos(pg, v2);
    if (pos1 == -1 || pos2 == -1)
        return;
?
    if (pg->edges[pos1][pos2] != INT_MAX)
        return;
?
    pg->edges[pos1][pos2] = pg->edges[pos2][pos1] = cost;
    ++pg->eSize;
}
?
// 普里姆算法的实现
void MiniSpanTree_Prim(AMGraph* pg, VertexType u)
{
    assert(pg);
    EdgeType* lowcostArr = (EdgeType*)malloc(sizeof(EdgeType) * pg->vSize);
    int* adjVexPosArr = (int*)malloc(sizeof(int) * pg->vSize);
    assert(lowcostArr && adjVexPosArr);
?
    int pos = GetVertexPos(pg, u);
    if (pos == -1)
        return;
    
    for (int i = 0; i < pg->vSize; ++i)
    {
        if (i != pos)
        {
            lowcostArr[i] = pg->edges[pos][i];
            adjVexPosArr[i] = pos;
        }
        else
        {
            lowcostArr[i] = 0; ?// 初始，U = {u}
        }
    }
    
 ? ?// 选择其余 pg->vSize - 1 个顶点，生成 pg->vSize - 1 条边
    for (int i = 0; i < pg->vSize - 1; ++i)
    {
        EdgeType min = INT_MAX;
        int minIndex = -1;
        for (int j = 0; j < pg->vSize; ++j)
        {
            if (lowcostArr[j] != 0 && lowcostArr[j] < min)
            {
                min = lowcostArr[j];
                minIndex = j;
            }
        }
        printf("(%c, %c)\n", pg->vertices[adjVexPosArr[minIndex]], pg->vertices[minIndex]);
        lowcostArr[minIndex] = 0; ?// 将顶点并入 U 
?
        for (int j = 0; j < pg->vSize; ++j)
        {
            if (pg->edges[minIndex][j] < lowcostArr[j])
            {
                lowcostArr[j] = pg->edges[minIndex][j];
                adjVexPosArr[j] = minIndex;
            }
        }
    }
 ? ?
 ? ?free(lowcostArr);
    free(adjVexPosArr);
}

Test.c：

#include "AMGraph.h"
#include <stdio.h>
?
int main()
{
    AMGraph g;
    AMGraphInit(&g);
    InsertVertex(&g, 'A');
    InsertVertex(&g, 'B');
    InsertVertex(&g, 'C');
    InsertVertex(&g, 'D');
    InsertVertex(&g, 'E');
    InsertVertex(&g, 'F');
    InsertEdge(&g, 'A', 'B', 6);
    InsertEdge(&g, 'A', 'C', 1);
    InsertEdge(&g, 'A', 'D', 5);
    InsertEdge(&g, 'B', 'C', 5);
    InsertEdge(&g, 'B', 'E', 3);
    InsertEdge(&g, 'C', 'D', 5);
    InsertEdge(&g, 'C', 'E', 6);
    InsertEdge(&g, 'C', 'F', 4);
    InsertEdge(&g, 'D', 'F', 2);
    InsertEdge(&g, 'E', 'F', 6);
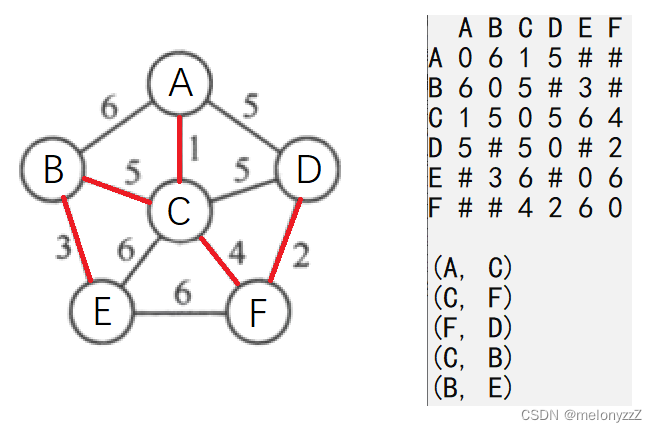
    ShowAdjMatrix(&g);
    printf("\n");
?
    MiniSpanTree_Prim(&g, 'A');
    return 0;
}

四、克鲁斯卡尔算法的构造过程

假设连通网 N = (V, E)。

令最小生成树的初始状态为只有 n 个顶点而无边的非连通图 T = (V, {})，图中每个顶点自成一个连通分量。
在 E 中选择权值（代价）最小的边，若该边依附的顶点落在不同的连通分量上（即不形成回路），则将此边加入到 T 中，否则舍去此边而选择下一条权值最小的边。
重复 2，直至 T 中所有顶点都在一个连通分量上为止。

例如，下图所示为依照克鲁斯卡尔算法对连通网 G5 构造一棵最小生成树的过程。权值 1、2、3、4 的 4 条边由于满足上述条件，则先后被加入到 T 中；权值为 5 的两条边 (v1, v4) 和 (v3, v4) 被舍去，因为它们依附的两顶点在同一连通分量上，它们若加入 T 中，则会使 T 中产生回路，而下一条权值（= 5）最小的边 (v2, v3) 联结两个连通分量，则可加入 T。由此，构造出了一棵最小生成树。

可以看出，克鲁斯卡尔算法逐步增加生成树的边，与普里姆算法相比，可称为 "加边法"。与普里姆算法一样，每次选择最小边时，可能有多条同样权值的边可选，可以任选其一。

五、克鲁斯卡尔算法的实现

假设无向网 G 以邻接矩阵形式存储，构造 G 的最小生成树，输出 T 的各条边。

typedef struct Edge
{
    int x; ?// 边的起点在图中的位置
    int y; ?// 边的终点在图中的位置
    EdgeType cost; ?// 边上的权值（即代价）
}Edge;
?
int CmpByCost(const void* e1, const void* e2)
{
    return (*(Edge*)e1).cost - (*(Edge*)e2).cost;
}
?
void MiniSpanTree_Kruskal(AMGraph* pg)
{
    assert(pg);
    Edge* edges = (Edge*)malloc(sizeof(Edge) * pg->eSize);
    assert(edges);
    int k = 0;
    for (int i = 0; i < pg->vSize; ++i)
    {
        for (int j = i + 1; j < pg->vSize; ++j)
        {
            if (pg->edges[i][j] != INT_MAX)
            {
                edges[k].x = i;
                edges[k].y = j;
                edges[k].cost = pg->edges[i][j];
                ++k;
            }
        }
    }
    qsort(edges, pg->eSize, sizeof(Edge), CmpByCost);
?
    int* vexSet = (int*)malloc(sizeof(int) * pg->vSize); ?// 标识各顶点所属的连通连通分量
    assert(vexSet);
    for (int i = 0; i < pg->vSize; ++i)
    {
        vexSet[i] = i;
    }
?
    for (int i = 0; i < pg->eSize; ++i)
    {
        int x = edges[i].x;
        int y = edges[i].y;
        int vs1 = vexSet[x];
        int vs2 = vexSet[y];
        if (vs1 != vs2)
        {
            printf("(%c, %c)\n", pg->vertices[x], pg->vertices[y]);
            for (int j = 0; j < pg->vSize; ++j)
            {
                if (vexSet[j] == vs2) ?
                    vexSet[j] = vs1;
            }
        }
    }
?
    free(edges);
    free(vexSet);
}

文章来源:https://blog.csdn.net/melonyzzZ/article/details/135041202
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！