逻辑回归中的损失函数

一、引言

????????逻辑回归中的损失函数通常采用的是交叉熵损失函数（cross-entropy loss function）。在逻辑回归中，我们通常使用sigmoid函数将线性模型的输出转换为概率值，然后将这些概率值与实际标签进行比较，从而计算损失。

二、交叉熵损失函数

????????在逻辑回归解决二分类问题的学习中，我们认识到逻辑回归的输出结果可以看成输入时输出为正例（)的概率。

分解如下：

????????于是我们便想到可以通过比较模型预测的概率分布和实际标签之间的差异来衡量模型的准确性。在信息论中，交叉熵用来比较两个概率分布之间的差异。

定义：交叉熵损失函数（Cross-entropy loss function）是一种用于衡量模型输出与实际标签之间差异的损失函数。在机器学习中，交叉熵损失函数通常用于分类问题中，特别是在逻辑回归和神经网络等模型中。

对于一个逻辑回归函数：

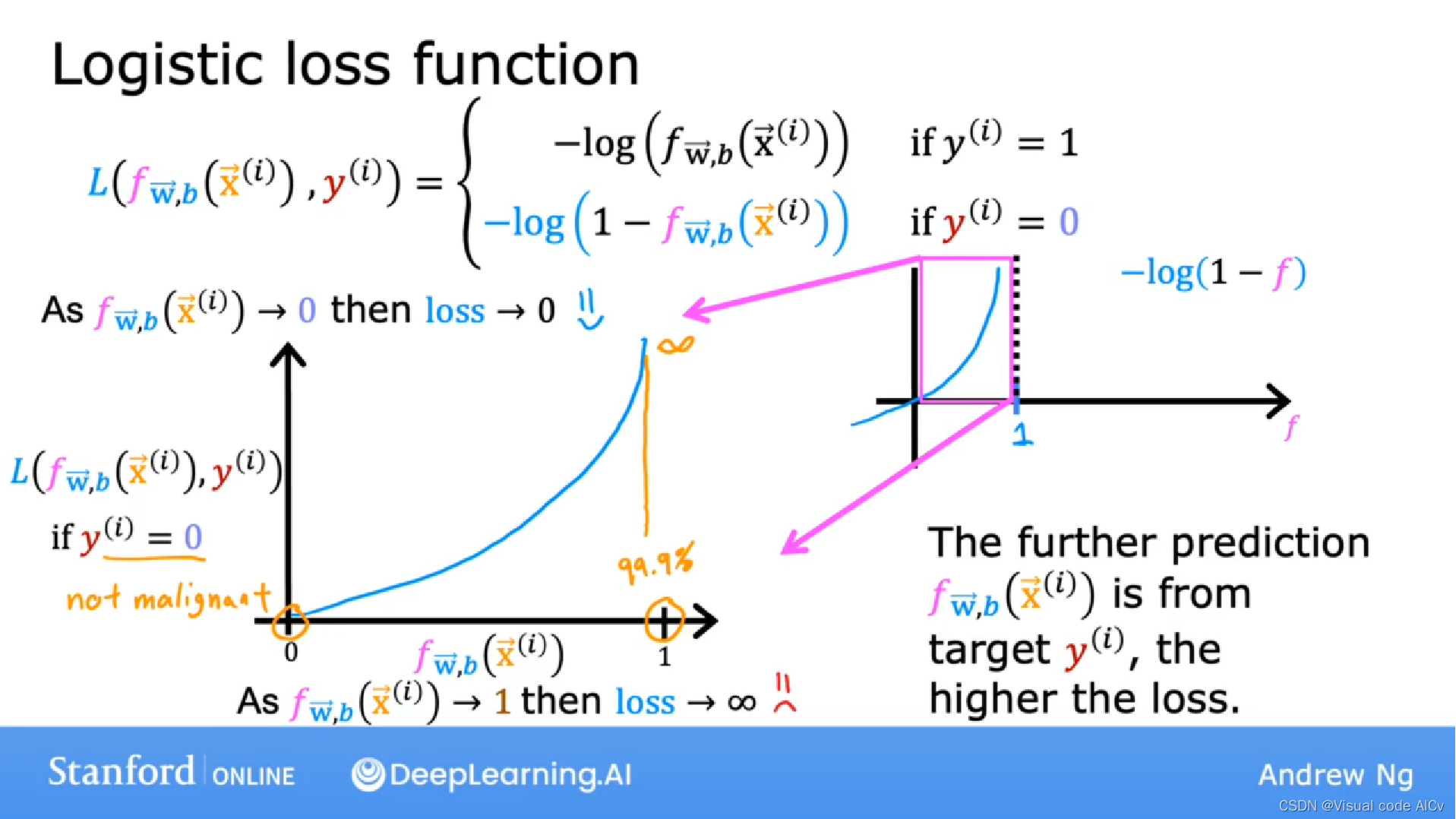
损失函数公式：? ?

简化后的公式：

根据损失函数的定义，当的值与目标值越接近，损失函数值越小，预测越准确。

所以：

? ??

三、为什么不使用均方差损失函数

非凸性：均方差损失函数在逻辑回归中会导致损失函数变成非凸函数，这会导致优化过程变得非常困难。因为非凸函数有多个局部最小值， 而均方差损失函数可能会陷入局部最小值而无法到达全局最小值，这回影响模型的训练效果。

?

输出范围不同：逻辑回归的输出是概率值，范围在0到1之间，而均方差损失函数对于这种概率输出不敏感，它对于离群值（outliers）非常敏感。这意味着即使是一个很小的偏离，也会导致损失函数变得非常大，从而使得模型对于异常值非常敏感。