最小生成树

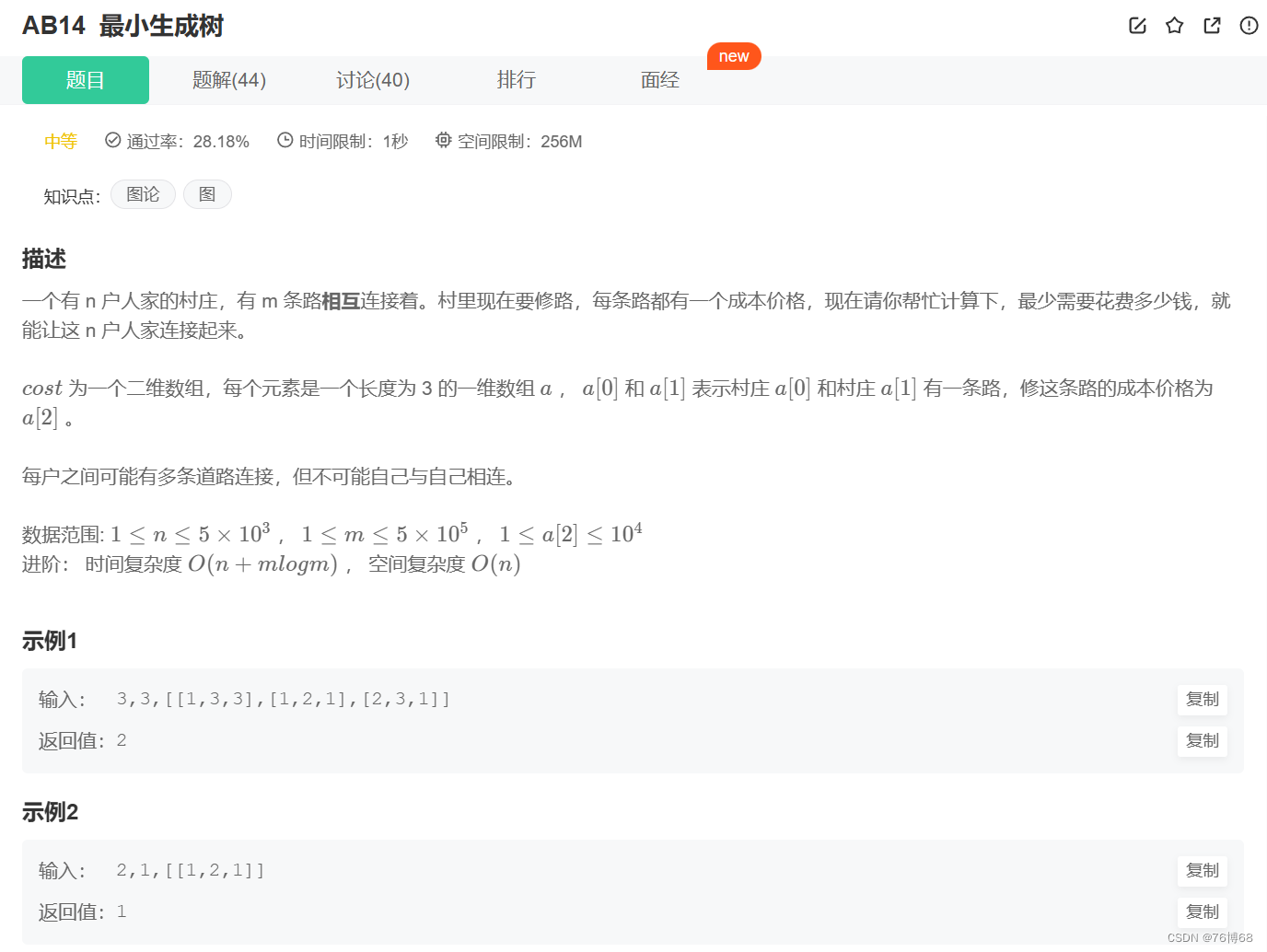
这段代码使用Kruskal 算法实现了一个找到无向图的最小生成树（Minimum Spanning Tree）的函数

#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
#include <limits.h>

// 定义边的结构体
struct Edge {
    int src, dest, weight;
};

// 定义图的结构体
struct Graph {
    int V, E;
    struct Edge* edges; // 保存图的所有边
};

// 创建图的函数
struct Graph* createGraph(int V, int E) {
    struct Graph* graph = (struct Graph*)malloc(sizeof(struct
                          Graph)); // 分配图的内存空间
    graph->V = V; // 图的顶点数
    graph->E = E; // 图的边数
    graph->edges = (struct Edge*)malloc(E * sizeof(struct
                                        Edge)); // 分配边数组的内存空间
    return graph;
}

// 寻找节点的根节点（用于判断两个节点是否属于同一个集合）
int findParent(int parent[], int i) {
    if (parent[i] == -1)
        return i;
    return findParent(parent, parent[i]);
}

// 合并两个集合
void unionSet(int parent[], int x, int y) {
    int xSet = findParent(parent, x);
    int ySet = findParent(parent, y);
    parent[xSet] = ySet;
}

// 用于 qsort 的比较函数，按照边的权重升序排序
// compareEdges 是比较函数，告诉 qsort 如何对边进行排序。
int compareEdges(const void* a, const void* b) {
    struct Edge* edgeA = (struct Edge*)a;
    struct Edge* edgeB = (struct Edge*)b;
    return edgeA->weight - edgeB->weight;
}

// 主函数，实现 Kruskal 算法找到最小生成树的总权重
int miniSpanningTree(int n, int m, int** cost, int costRowLen,
                     int* costColLen ) {
    // 创建图
    struct Graph* graph = createGraph(n, m);

    // 将输入转换为图的边集合
    for (int i = 0; i < m; ++i) {
        graph->edges[i].src = cost[i][0] - 1;
        graph->edges[i].dest = cost[i][1] - 1;
        graph->edges[i].weight = cost[i][2];
    }

    int V = graph->V; // 顶点数
    int E = graph->E; // 边数

    // qsort 是 C 语言中的一个标准库函数，用于对数组进行快速排序。
    // compareEdges 是比较函数，告诉 qsort 如何对边进行排序。
// 如果 a 应排在 b 之前，则返回负数。
// 如果 a 和 b 相同，则返回零。
// 如果 a 应排在 b 之后，则返回正数。
    qsort(graph->edges, E, sizeof(struct Edge),
          compareEdges); // 对边按权重排序

    int parent[V]; // 用于记录节点的父节点
    // memset(parent, -1, sizeof(parent)) 的意思是将 parent 数组中的所有元素设置为 -1，sizeof(parent) 表示需要设置的内存大小，即数组 parent 的总字节数。
    memset(parent, -1, sizeof(
               parent)); // 初始化节点的父节点为 -1，表示各自是独立的集合

    int totalCost = 0; // 记录最小生成树的总权重
    int e = 0; // 边的计数器
    int edgesConsidered = 0; // 已考虑的边的计数器

    // 进行 Kruskal 算法，逐个考虑边
    while (edgesConsidered < V - 1) {
        struct Edge nextEdge = graph->edges[e++];
        int x = findParent(parent, nextEdge.src);
        int y = findParent(parent, nextEdge.dest);

        // 判断两个节点是否属于同一个集合，如果不是，则将这两个节点合并到一个集合中，并将边的权重添加到总权重中
        if (x != y) {
            totalCost += nextEdge.weight;
            unionSet(parent, x, y);
            edgesConsidered++;
        }
    }

    free(graph->edges); // 释放边数组内存
    free(graph); // 释放图的内存

    // 如果最终形成的最小生成树的边数不是 V-1，则说明图不是完全连接的，返回 -1 表示无法构建最小生成树
    if (edgesConsidered != V - 1) {
        return -1; // 图不是完全连接的
    }

    return totalCost; // 返回最小生成树的
}