Python数据分析案例35——多元线性回归全流程 (数据探索可视化，回归分析，多重共线性，残差检验，异方差检验，自相关检验)

案例背景

很多经济学同学用Python做传统统计学的回归分析时可能没有R或者Stata，Eviews，SPSS方便，他们对回归分析里面常用的检验过程不熟悉。

Python做回归这些当然没有这些统计学，计量经济学常用的软件方便，但是都能做，只是没有人总结一个系统的完整的回归分析的流程。他们做回归往往忽略了，传统统计学还需要做的多重共线性的检验，残差检验，异方差检验，自相关检验等等。

本次案例就来总结一下一个传统的，经典的多元线性回归应该包含哪些流程，以及Python代码怎么做。

---

数据介绍

本次案例来自于同学总结得一个经济学很典型的数据，包括不同年份的[农业，原料，贷款，产品，就业，薪酬]等指标。目的就是研究这些不同指标对于农业化指数的影响程度。

简单来说，就是y是农业，x是其他变量。

需要本次演示的数据和全部代码的来练习的同学可以参考：回归数据

---

代码实现

还是先导入包：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt 
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
pd.set_option('display.float_format', lambda x: '{:.4f}'.format(x))

读取数据，将年份设置为索引

df=pd.read_excel('数据.xlsx').dropna(axis=1).set_index('year')
df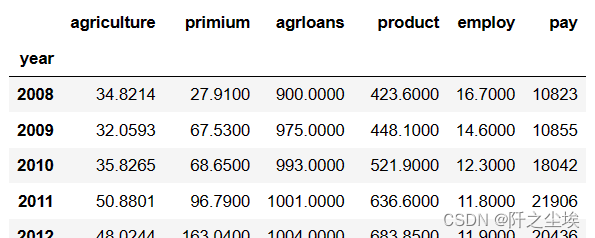

数据还是很整洁的。标准的表格数据。

描述性统计

计算简单的几个统计量：

df.describe().T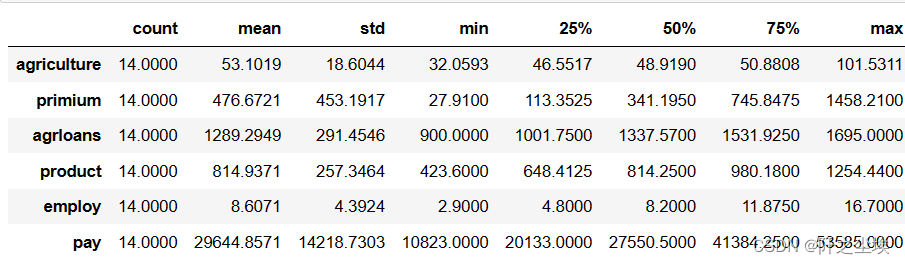

画出散点图

y = df['agriculture']
x_cols = ['primium', 'agrloans', 'product', 'employ', 'pay']
x = df[x_cols]
fig = plt.figure(figsize=(8,4), dpi=128)  
for i in range(5):
    plt.subplot(2,3,i + 1)  # 2行3列子图
    sns.scatterplot(x=x.iloc[:, i], y=y)
    #plt.ylabel(column[i], fontsize=12)
    #plt.xticks([])
plt.tight_layout()
plt.savefig('散点图.jpg',dpi=128)
plt.show()

可以看到五个自变量其中除了employ外，其他和agriculture都是正相关，而且相关性还挺高的样子，明显有着一个回归线的趋势。

进一步查看数据的分布，画出箱线图：

column = df.columns.tolist() # 列表头
fig = plt.figure(figsize=(6,6), dpi=128)  # 指定绘图对象宽度和高度
for i in range(6):
    plt.subplot(3,2,i + 1)  # 2行3列子图
    sns.boxplot(data=df.iloc[:,i].to_numpy(), orient="v",width=0.5)  # 箱式图
    plt.ylabel(column[i], fontsize=12)
    plt.xticks([])
plt.tight_layout()
plt.savefig('箱线图.jpg',dpi=128)
plt.show()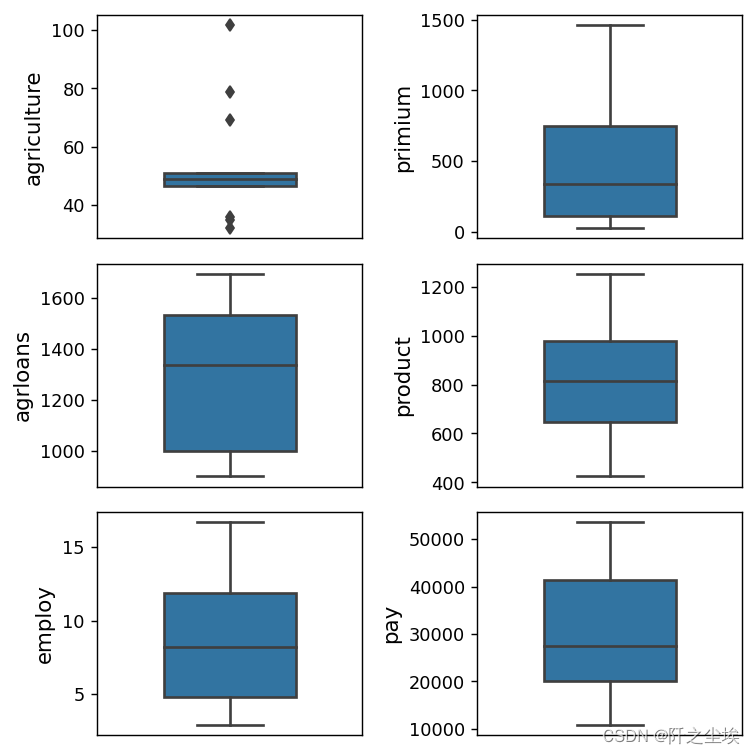

除了y自己外，其他的x的分布都较为对称，符合正态分布的假定。

---

相关性分析

计算相关系数矩阵：

df.corr()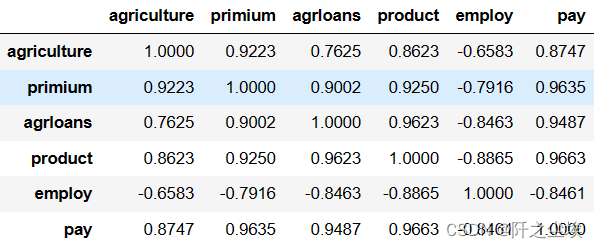

画出热力图：

plt.figure(figsize=(7,5),dpi=128)
sns.heatmap(df.corr().round(2), cmap='coolwarm', annot=True, annot_kws={"size": 10})
plt.savefig('相关系数.jpg')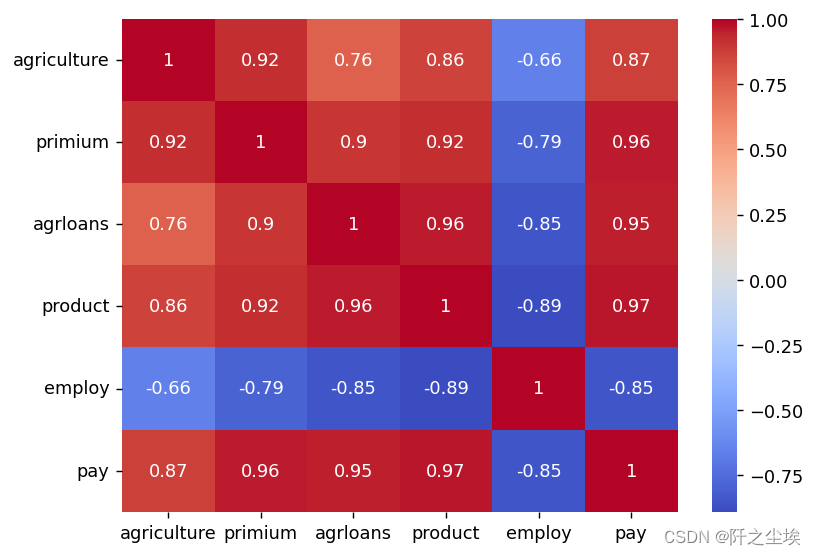

?

employ和其他变量都是负相关，agriculture和x之间都有高度的相关性，但是X们间也存在高度的相关，例如primium和其他四个x相关系数都高达0.9以上，

说明模型可能存在多重共线性。

---

最小二乘线性回归

开始ols，多元线性回归

model = smf.ols('agriculture~primium+agrloans+product+employ+pay', data=df)
model = model.fit()
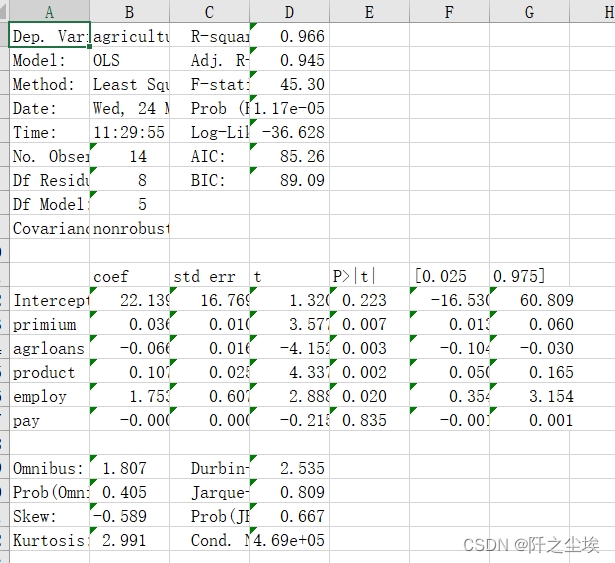
model.summary()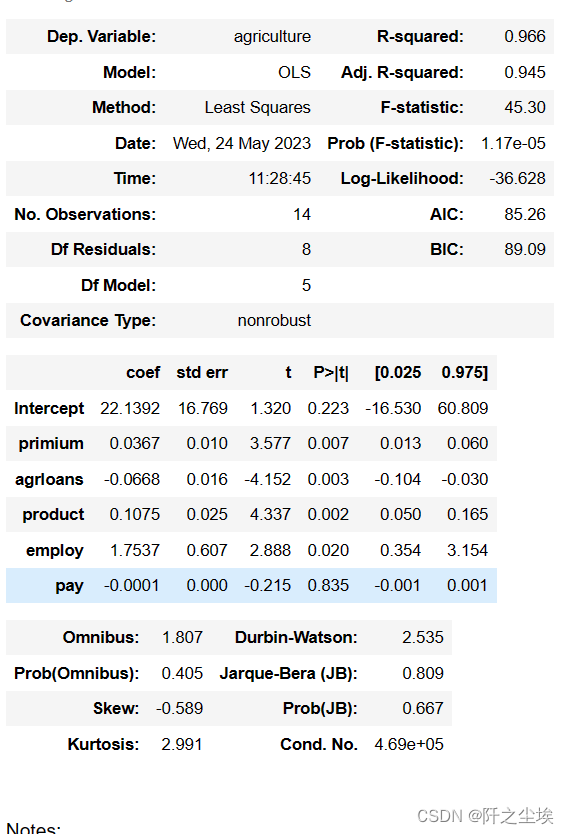

“整体上，该模型具有很高的解释力，R平方值为0.966，说明模型能够解释大部分农业的变异。调整后的R平方值为0.945，略低于R平方，但依然表明模型非常有效。

F统计量为45.30，其对应的概率为1.17e-05，这非常低，表明模型至少有一个预测变量对于解释农业是显著的。模型中共有14个观测值，5个自变量（模型自由度为5）和8个残差自由度。

系数部分显示，“primium”（每单位变化）预计会使“agriculture”增加0.0367单位，且在统计上显著（p=0.007）。相反，“agrloans”每单位增加预计会使“agriculture”减少0.0668单位，并且这个效应也是显著的（p=0.003）。 “product”每单位增加预计会使“agriculture”增加0.1075单位，同样显著（p=0.002）。 “employ”预计对“agriculture”的影响是正向的，每单位增加将使“agriculture”增加1.7537单位，这个效应在统计上也是显著的（p=0.020）。最后，“pay”变量对“agriculture”的影响不显著（p=0.835）。

该模型的Durbin-Watson统计量为2.535，接近2，表明数据中不存在自相关问题。Jarque-Bera检验表明残差正态分布的假设不能被拒绝，意味着模型残差近似正态分布。条件数为4.69e+05，表明可能存在多重共线性问题，这可能需要进一步检查。

综上所述，这个模型在统计上是有效的，但需要注意潜在的多重共线性问题。多数变量对农业的影响是显著的，但“pay”变量的影响不显著。”

省流版：

模型的拟合优度高达96%，调整后的R2为0.945。说明这几个解释变量能高度解释y的变化.整体的F值为45.30，远超临界值，说明模型整体很显著。

在0.05 的显著性水平下，除了pay，其他四个变量都是显著的，说明他们的变化对y产生了显著性影响。

再来看单个变量的系数，其中employ系数为正，agrloans系数负，这些不符合理论期望，应该是模型存在多重共线性导致的。

计算方差膨胀因子，查看多重共线性。

---

方差膨胀因子(VIF)

?定义VIF计算的函数

def VIF_calculate(df_all,y_name):
    x_cols=df.columns.to_list()
    x_cols.remove(y_name)
    
    def vif(df_exog,exog_name):
        exog_use = list(df_exog.columns)
        exog_use.remove(exog_name)
        model=smf.ols(f"{exog_name}~{'+'.join(list(exog_use))}",data=df_exog).fit()
        return 1./(1.-model.rsquared)

    df_vif=pd.DataFrame()
    for x in x_cols:
        df_vif.loc['VIF',x]=vif(df_all[x_cols],x)
        
    df_vif.loc['tolerance']=1/df_vif.loc['VIF']
    df_vif=df_vif.T.sort_values('VIF',ascending=False)
    df_vif.loc['mean_vif']=df_vif.mean()
    return df_vif

计算

VIF_calculate(df,'agriculture')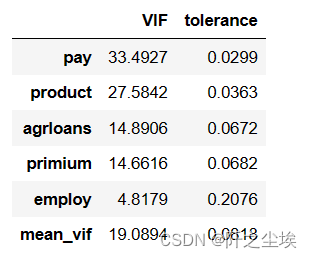

一般认为VIF值大于10，模型就会存在多重共线性。除了employ变量，其他四个变量之间都存在多重共线性的问题。

---

残差检验

画出残差图：

plt.rcParams ['font.sans-serif'] =['SimHei']
plt.rcParams['axes.unicode_minus']=False
 
x=model.fittedvalues;y=model.resid
 
plt.subplots(1,2,figsize=(8,3),dpi=128)
plt.subplot(121)
plt.scatter(model.fittedvalues,model.resid)
plt.xlabel('拟合值')
plt.ylabel('残差')
plt.title('(a)残差值与拟合值图',fontsize=15)
plt.axhline(0,ls='--')
 
ax2=plt.subplot(122)
pplot=sm.ProbPlot(model.resid,fit=True)
pplot.qqplot(line='r',ax=ax2,xlabel='期望正态值',ylabel='标准化的观测值')
ax2.set_title('(b)残差正态Q-Q图',fontsize=15)
plt.show()

?残差均匀分布在0轴附近，模型不存在异方差等问题。

---

异方差的white检验

from statsmodels.stats.diagnostic import het_white
wh = het_white(model.resid, model.model.exog)
print('LM Statistic: {:.3f}'.format(wh[0]))
print('LM p-value: {:.3f}'.format(wh[1]))
#print('F Statistic: {:.3f}'.format(wh[2]))   print('F p-value: {:.3f}'.format(wh[3]))

white检验的p值大于0.05,模型无异方差。

---

自相关的DW检验

from statsmodels.stats.stattools import durbin_watson
dw = durbin_watson(model.resid)
print('DW statistic: {:.4f}'.format(dw))

DW的值接近2，模型无自相关。

---

处理多重共线性的问题

出现多重共线性问题时，可以采取以下几种方法进行处理：

1.删除相关性较强的变量。如果两个或多个自变量之间存在高度相关性，则可能会导致多重共线性问题。可以通过计算自变量之间的相关系数矩阵，然后删除其中相关性较强的变量，以降低共线性的影响。

2.主成分分析（PCA）。主成分分析可以将多个相关性较强的自变量转化为少数几个不相关的主成分，从而降低共线性的影响。可以使用Python中的sklearn.decomposition.PCA类进行主成分分析。

3.岭回归（Ridge Regression）。岭回归是一种正则化方法，可以通过在损失函数中增加一个惩罚项来避免过拟合。在存在多重共线性的情况下，使用岭回归可以降低模型方差，提高模型的泛化性能。

4.Lasso回归（Lasso Regression）。Lasso回归也是一种正则化方法，可以通过对回归系数的L1范数进行惩罚来实现特征选择和降维。Lasso回归可以通过缩小相关性较强的自变量的系数来降低多重共线性的影响。

5.收集更多数据。如果多重共线性问题来自于数据样本的局限性，那么可以通过收集更多的数据来缓解该问题。

（计量经济学应该只学了岭回归，就用这个吧。主成分是传统统计学学的，Lasso回归也是经典的统计学结合机器学习方法，一般的经济学学生不懂。）

---

岭回归

构建模型，拟合

y = df['agriculture']
X = df[['primium', 'agrloans', 'product', 'employ', 'pay']]
from sklearn.linear_model import Ridge
model_ride = Ridge(alpha=10)
#拟合模型
model_ride .fit(X, y)
#计算测试集上的拟合优度
model_ride .score(X, y)

拟合优度和前面差不多。

模型截距

model_ride .intercept_

#模型系数 
#数据框展示系数
pd.DataFrame(model_ride.coef_, index=X.columns, columns=['Coefficient'])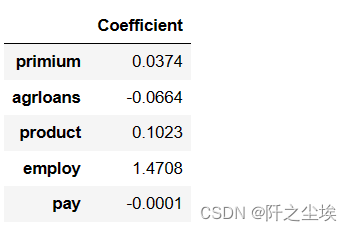

与普通ols相比系数缩小了一点，结果会好一点。至于这个模型的参数估计，假设检验那些东西，岭回归这个模块里面没有很简便的接口，就不做演示了。

---

结果存储

我们上面做的最小二乘的回归结果还没进行储存，怎么变成excel进行储存呢？我定义了一个简单的函数：

def 储存(writer,model,model_name='model_SH1'):
    df1 = pd.DataFrame(model.summary().tables[0])
    df2 = pd.DataFrame(model.summary().tables[1])
    df3 = pd.DataFrame(model.summary().tables[2])
    df1.to_excel(writer, sheet_name=model_name, startrow=0, startcol=0, header=False, index=False)
    df2.to_excel(writer, sheet_name=model_name, startrow=df1.shape[0]+1, startcol=0, header=False, index=False)
    df3.to_excel(writer, sheet_name=model_name, startrow=df1.shape[0]+df2.shape[0]+2, startcol=0, header=False, index=False)

然后储存：

model_list=['model']
with pd.ExcelWriter('回归表.xlsx') as writer:
    for model_name in model_list:
        model=eval(model_name)
        储存(writer,model=model,model_name=model_name)

然后就可以在excel里面查看了，也方便复制到word里面去。?

---

创作不易，看官觉得写得还不错的话点个关注和赞吧，本人会持续更新python数据分析领域的代码文章~