基于[Discretized] Torus的全同态加密指引（2）

前序博客有：

• 基于[Discretized] Torus的全同态加密指引（1）

5. 基于已加密数据处理

很显然，TLWE加密方案和TGLWE加密方案均具有加法同态性。[GSW13] Gentry–Sahai–Waters 方法使用matrix product来将TLWE加密方案和TGLWE加密方案，转换为支持有限乘法次数的方案。

5.1 TLWE密文

5.1.1 TLWE密文加法

令（${\mathbb{T}}_q^{n+1}$中的）${\mathbf{c}}_1\leftarrow TLW{E}_{\mathbf{s}}({\mu }_1)$和${\mathbf{c}}_2\leftarrow TLW{E}_{\mathbf{s}}({\mu }_2)$，分别为（$\mathcal{P}$中）${\mu }_1,{\mu }_2$的TLWE加密：
${\mathbf{c}}_1=(a_1,?,a_n,b),{\mathbf{c}}_2=(a_1^{\prime },?,a_n^{\prime },b^{\prime })$
其中：

• $(a_1,?,a_n)\stackrel{\S }{\leftarrow }{\mathbb{T}}_q^n$，$b={\sum }_{j=1}^n{s}_j?a_j+{\mu }_1+e_1$
• $(a_1^{\prime },?,a_n^{\prime })\stackrel{\S }{\leftarrow }{\mathbb{T}}_q^n$，$b^{\prime }={\sum }_{j=1}^n{s}_j?a_j^{\prime }+{\mu }_2+e_2$
• $e_1,e_2$均为“small”。

则有：

• （${\mathbb{T}}_q^{n+1}$中的）${\mathbf{c}}_3:={\mathbf{c}}_1+{\mathbf{c}}_2$ 为（$\mathcal{P}$中）${\mu }_3:={\mu }_1+{\mu }_2$的有效加密。
  即：
  

密文的加法，解释了为何在TLWE加密定义中，选择$\mathcal{P}$为${\mathbb{T}}_q$的加法子群。这样，就暗示了，若${\mu }_1,{\mu }_2\in \mathcal{P}$，则有${\mu }_3={\mu }_1+{\mu }_2\in \mathcal{P}$。

5.1.2 TLWE密文与某已知常量值的乘法

与某常量值的乘法，可通过一系列加法来实现。因此，已知$\mu \in \mathcal{P}$的TLWE密文$\mathbf{c}\leftarrow TLW{E}_{\mathbf{s}}(\mu )$，对于某已知（small）整数$K\ne 0$：

• 若$K>0$，则$K?\mu$的TLWE密文可表示为：
  
• 若$K<0$，则$K?\mu$的TLWE密文可表示为：$K?\mathbf{c}=(?K)?(?\mathbf{c})$。

更准确来说，是将$\mathbf{c}$向量中的每个元素与$K$相乘，即若$\mathbf{c}=(a_1,?,a_n,b)\in {\mathbb{T}}_q^{n+1}$，则有：
$K?\mathbf{c}=(K?a_1,?,K?a_n,K?b)$。

只要最终的噪声仍是“small”的，则（${\mathbb{T}}_q^{n+1}$中的）$K?\mathbf{c}\leftarrow TLW{E}_{\mathbf{s}}({\mu }_1)$为（$\mathcal{P}$中的）$K?\mu$的有效TLWE加密。

5.1.3 TLWE密文之间的乘法运算

对已加密数据操作的主要调整，在于密文间的乘法运算。
为让[GSW13] Gentry–Sahai–Waters 方法可行，需将TLWE所加密的密文以矩阵表示。

Gadget matrix：
Flattening：

• 为不影响dot products而修改vectors的方法[BGV14, Bra12]
• 有助于控制noise

接下来展示基于discretized torus ${\mathbb{T}}_q=q^{?1}\mathbb{Z}/\mathbb{Z}$，其中$q$为通用整数（即无需为power of 2），的“gadget decomposition”技术。
对于某radix $B$和整数$l\ge 1$，其满足$B^l|q$，对于gadget matrix ${\mathbf{G}}^{(n+1)\times (n+1)l}$有：

其中$\mathbf{g}=(1/B,?,1/B^l)\in {\mathbb{T}}_q^l$，因此：

• 对于输入向量$\mathbf{u}\in {\mathbb{Z}}^{(n+1)l}$，product ${\mathbf{u}?\mathbf{G}}^T$的结果为${\mathbb{T}}_q^{n+1}$中向量。
• 对于逆变换${\mathbf{G}}^{?1}:{\mathbb{T}}_q^{n+1}\to {\mathbb{Z}}^{(n+1)l}$，对任意向量$\mathbf{v}\in {\mathbb{T}}_q^{n+1}$，有：
  ${\mathbf{G}}^{?1}(\mathbf{v})?{\mathbf{G}}^T\approx \mathbf{v}$且${\mathbf{G}}^{?1}(\mathbf{v})$为“small”。
  该逆变换，会将向量中的每个元素替换为其signed radix-$B$ expansion。
  准确来说，若$\mathbf{v}=(v_1,?,v_{n+1})\in {\mathbb{T}}_q^{n+1}$，其中$v_i\in [?\frac{1}{2},\frac{1}{2})$，设置${\bar{v}}_i=?B^l{v}_i?$，并表示成：
  ${\bar{v}}_i\equiv {\sum }_{j=1}^l{u}_{i,j}{B}^{l?j}(\mathrm{mod}{B}^l)$，其中$u_{i,j}\in [??B/2?,?B/2?)$。
  定义${\mathbf{g}}^{?1}(v_i)=(u_{i,1},?,u_{i,l})\in {\mathbb{Z}}^l$，则有：
  $$\begin{gathered} {\mathbf{G}}^{?1}(\mathbf{v}):=({\mathbf{g}}^{?1}(v_1),{\mathbf{g}}^{?1}(v_2),?,{\mathbf{g}}^{?1}(v_{n+1})) \\ =(u_{1,1},?,u_{1,l},u_{2,1},?,u_{2,l},?,u_{n+1,1},?,u_{n+1,l})\in {\mathbb{Z}}^{(n+1)l} \end{gathered}$$。
  注意，当$B^l=q$时，$\mathbf{v}$中所有元素$v_i\in [?\frac{1}{2},\frac{1}{2})$均满足${\bar{v}}_i=B^l{v}_i$。然后基于${\mathbb{T}}_q$，有${\mathbf{G}}^{?1}(\mathbf{v})?{\mathbf{G}}^T=\mathbf{v}$成立。

举例：

Remark 5：
逆变换${\mathbf{G}}^{?1}$自然扩展了矩阵。对于矩阵$\mathbf{M}\in {\mathbb{T}}_q^{m\times (n+1)}$，对应的${\mathbf{G}}^{?1}(\mathbf{M})\in {\mathbb{Z}}^{m\times (n+1)l}$定义为$m\times (n+1)l$矩阵，其第$\#i$行为${\mathbf{G}}^{?1}(m_i)$，其中$m_i$为$\mathbf{M}$的第$\#i$行。满足${\mathbf{G}}^{?1}(\mathbf{M})?\mathbf{G}\approx \mathbf{M}$。

TGSW encryption加密方案：

• gadget matrix可构建基于torus的Gentry–Sahai–Waters（GSW）加密方案变种。

令整数$p|q$，其中$q=2^{\Omega }$。基于${\mathbb{T}}_q$的gadget decomposition中，整数$B,l$满足$B^l|q$。${\mathbf{G}}^T$中所有值要么为0，要么为$B^{?j}$格式，其中$1\le j\le l$。
gadget matrix $\mathbf{G}$实际是基于$B^{?l}\mathbb{Z}/\mathbb{Z}?{\mathbb{T}}_q$定义的。

TGSW encryption加密方案中假设$p=B^l$，gadget matrix $\mathbf{G}$实际是基于${\mathbb{T}}_p=p^{?1}\mathbb{Z}/\mathbb{Z}$定义的。
私钥为$\mathbf{s}=(s_1,?,s_n)\in {\mathbb{B}}^n$，明文空间为$\bar{\mathcal{P}}:=\mathbb{Z}/p\mathbb{Z}$。用私钥$\mathbf{s}$对$m\in \bar{\mathcal{P}}$的TGSW加密定义为：
$TGS{W}_{\mathbf{s}}(m)=\mathbf{Z}+m?{\mathbf{G}}^T(\in {\mathbb{T}}_q^{(n+1)l\times (n+1)})$
其中：

$TGS{W}_{\mathbf{s}}(m)\in {\mathbb{T}}_q^{(n+1)l\times (n+1)}$中最后一行是$TLW{E}_{\mathbf{s}}(0)+m?(0,?,0,\frac{1}{B^l})\in {\mathbb{T}}_q^{n+1}$，即为对$\mu :=\frac{m}{B^l}\in \mathcal{P}$的TLWE encryption，其中$\mathcal{P}={\mathbb{T}}_p$。

TGSW明文基于ring $\bar{\mathcal{P}}=\mathbb{Z}/p\mathbb{Z}$定义。对于$m_1,m_2\in \bar{\mathcal{P}}$，及其相应的密文${\mathbf{C}}_1\leftarrow TGS{W}_{\mathbf{s}}(m_1)$和${\mathbf{C}}_2\leftarrow TGS{W}_{\mathbf{s}}(m_2)$。令${\mathbf{C}}_3={\mathbf{C}}_1?{\mathbf{C}}_2:={\mathbf{G}}^{?1}({\mathbf{C}}_2)?{\mathbf{C}}_1$——这就是密文的[internal] product [GSW13, AP14, DM15]。
可验证${\mathbf{C}}_3={\mathbf{C}}_1?{\mathbf{C}}_2$为具有一定rounding error 和 multiplicative noise的$m_3=m_1\times m_2(\mathrm{mod}p)$的TGSW。
对应的证明为：

若$\mathbf{Z}\in {\mathbb{T}}_q^{(n+1)\times (n+1)}$矩阵各行为对$0$的TLWE加密，则对于任意（small）矩阵$\mathbf{A}\in {\mathbb{Z}}^{m\times (n+1)}$，矩阵${\mathbf{Z}}^{\prime }=\mathbf{A}?\mathbf{Z}\in {\mathbb{T}}_q^{m\times (n+1)}$中各行为TLWE encryption of 0（up to the noise）。

举个例子：

注意，以上证明中，${\mathbf{Z}}_3$中的错误项由三部分组成：

• 1）源自${\mathbf{Z}}_1$的噪声，放大了${\mathbf{G}}^{?1}({\mathbf{C}}_2)$倍。
  倍乘的噪声增长很快。不过若所使用的gadget矩阵满足${\Vert \begin{array}{c}{\mathbf{G}}^{?1}({\mathbf{C}}_2)\end{array}\Vert }_{\infty }\le B/2$。
• 2）源自${\mathbf{Z}}_2$的噪声，放大了$m_1$倍。
• 3）源自rounding error ${?}_2$，放大了$m_1$倍。

若明文$m_1$保持small（如限定$m_1$为 { 0 , 1 } \{0,1\} {0,1}中元素），则上面2）3）项的噪声和错误也可控制住。

密文的external product：
TLWE密文要远短于TGSW密文，因此优选TLWE密文。

• 对于某正数$m_1\in \bar{\mathcal{P}}$和明文${\mu }_2\in \mathcal{P}?{\mathbb{T}}_q$可将TLWE看成是明文的external product：$m_1?{\mu }_2$。
• 对应$m_1?{\mu }_2$的密文external product，以$?$来表示：
  $?:TGSW\times TLWE\to TLWE,({\mathbf{C}}_1,{\mathbf{c}}_2)?{\mathbf{C}}_1?{\mathbf{c}}_2={\mathbf{G}}^{?1}({\mathbf{c}}_2)?{\mathbf{C}}_1$

其中：

• ${\mathbf{C}}_1\leftarrow TGS{W}_{\mathbf{s}}(m_1)$，其中$m_1\in \bar{\mathcal{P}}$。有：
  ${\mathbf{C}}_1={\mathbf{Z}}_1+m_1?{\mathbf{G}}^T\in {\mathbb{T}}_q^{(n+1)l\times (n+1)}$，其中：
  • ${\mathbf{Z}}_1=\left(\begin{array}{cccc}{a}_{1,1}& ?& a_{1,n}& b_1\\ a_{2,1}& ?& a_{2,n}& b_2\\ ?& & ?& ?\\ a_{(n+1)l,1}& ?& a_{(n+1)l,n}& b_{(n+1)l}\end{array}\right)$
  • $\{\begin{array}{c}(a_{i,1},?,a_{i,n})\stackrel{\S }{\leftarrow }{\mathbb{T}}_q^n\\ b_i={\sum }_{j=1}^n{s}_j?a_{i,j}+(e_1{)}_i\end{array}$
  • 对于$1\le i\le (n+1)l$，$(e_1{)}_i$为“small”的。
• ${\mathbf{c}}_2\leftarrow TLW{E}_{\mathbf{s}}({\mu }_2)$，其中${\mu }_2\in \mathcal{P}$。有：
  ${\mathbf{c}}_2=(a_1^{\prime },?,a_n^{\prime },b^{\prime })$，其中：
  • $\{\begin{array}{c}(a_1^{\prime },?,a_n^{\prime })\stackrel{\S }{\leftarrow }{\mathbb{T}}_q^n\\ b^{\prime }={\sum }_{j=1}^n{s}_j?a_j^{\prime }+{\mu }_2+e_2\end{array}$
  • $e_2$为“small”的。

从而有：

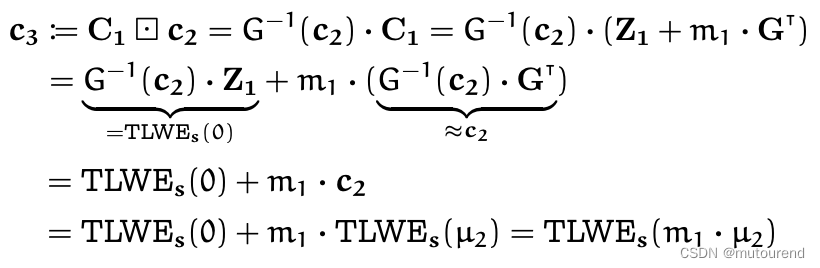
为对${\mu }_3:=m_1?{\mu }_2\in \mathcal{P}$的有效valid TLWE加密，若满足如下条件：

• 1）rounding error ${\Vert \begin{array}{c}{\mathbf{G}}^{?1}({\mathbf{c}}_2)?{\mathbf{G}}^T?{\mathbf{c}}_2\end{array}\Vert }_{\infty }$保持“small”。
• 2）倍乘后的噪声$e_3:={\mathbf{G}}^{?1}({\mathbf{c}}_2)?{\mathbf{e}}_1^T+m_1?e_2$保持“small”，其中${\mathbf{e}}_1=((e_1{)}_1,?,(e_1{)}_{(n+1)l})$。

5.2 TGLWE密文

TLWE和TGSW的底层计算和运算可扩展到多项式。以Torus多项式来替换Torus元素。加法和外乘做模$X^N+1$。使用（基于${\mathbb{T}}_{N,q}[X]$）的gadget matrix来控制噪声增长。

5.2.1 TGLWE密文加法运算

5.2.2 TGLWE密文与已知多项式的乘法运算

5.2.3 TGLWE密文之间乘法运算

相应的gadget matrix为：

需注意，TGLWE密文，可看成是：$TGLW{E}_{\mathfrak{s}}(\mathfrak{u})\equiv TGLW{E}_{\mathfrak{s}}(0)+(0,?,0,1)?\mathfrak{u}$。
相应的TGGSW密文定义为：

TGGSW密文与TGLWE密文的external product运算定义为：【结果为某TGLWE密文】

TFHE中，TGGSW密文与TGLWE密文的external product运算，的主要应用场景为：

• “controlled” multiplexer，或简称为CMUX。

具体为：

• 已知2个TGLWE密文${\mathfrak{c}}_0\leftarrow TGLW{E}_{\mathfrak{s}}({\mathfrak{u}}_0)$和${\mathfrak{c}}_1\leftarrow TGLW{E}_{\mathfrak{s}}({\mathfrak{u}}_1)$
• CMux operator，用作selector，根据某control bit b ∈ { 0 , 1 } b\in\{0,1\} b∈{0,1}的TGGSW密文${\mathfrak{C}}_b\leftarrow TGLW{E}_{\mathfrak{s}}(b)$，在${\mathfrak{c}}_0$和${\mathfrak{c}}_0$之间做选择。
• 可通过如下external product来实现：【其输出即为${\mathfrak{u}}_b$的TGLWE密文。】
  

5.3 基于已加密数据处理注意事项

对整数模$p$的编码（包括$p=2$的情况），见 论文 Guide to Fully Homomorphic Encryption over the [Discretized] Torus 2.2节。

这种编码是同态的，并遵循加密的同态结构。
具体为：【同理，这些编码对论文 Guide to Fully Homomorphic Encryption over the [Discretized] Torus 2.2节 固定精度的torus元素也成立。】

• 对任意的$i_1,i_2\in \mathbb{Z}/p\mathbb{Z}$。令$i_3=i_1+i_2\mathrm{mod}p$，有$Encode(i_3)=Encode(i_1)+Encode(i_2)$ in ${\mathbb{T}}_p$。
• 对任意的$i\in \mathbb{Z}/p\mathbb{Z}$和整数$k$。令$i_k=k?i\mathrm{mod}p$，有$Encode(i_k)=k?Encode(i)$ in ${\mathbb{T}}_p$。

6. Programmable Bootstrapping可编程自举

之前已提及，TLWE和TGLWE加密均需要实现特定操作——bootstrapping自举：

• 其核心为刷新含噪声的TLWE密文
• 应可编程，以同时对某选定函数进行evaluate。

6.1 Gentry’s Recryption

对于（对称）全同态加密算法$Encrypt$：

• 已知，私钥$sk$对$x$的密文$Encryp{t}_{sk}(x)$
• 对某单变量函数$f$的同态evaluation结果为，对$f(x)$的密文$Encryp{t}_{sk}(f(x))$

[Gen10] Gentry用于降低密文中噪声的核心思想为：采用采用同态加密自身的解密密钥，来对密文的解密进行同态evaluate。该解密密钥的加密（与用于生成密文的加密密钥匹配），构成了bootstrapping key自举密钥。

令：

• $c\leftarrow \mathfrak{E}ncryp{t}_{s{k}_1}(m)$：表示对明文$m$的有噪声密文加密。
• $bsk\leftarrow Encryp{t}_{s{k}_2}(s{k}_1)$：表示自举密钥。

假设上图中的$f$函数，为针对密文$c$的解密函数，可将其看成是单变量函数$\mathfrak{D}ecrypt(?,c)$。则令$x=s{k}_1$，对$f$的同态evaluation值为：
$Encryp{t}_{s{k}_2}(f(x))=Encryp{t}_{sk2}(\mathfrak{D}ecrypt(s{k}_1,c))=Encryp{t}_{s{k}_2}(m)$
整个流程如下图所示：

针对有噪声密文$c\leftarrow \mathfrak{E}ncryp{t}_{s{k}_1}(m)$，该recryption流程输出，对相同明文$m$加密的 新密文$Encryp{t}_{s{k}_2}(m)$。注意，这2个加密密钥是不同的。加密算法$Encrypt$和$\mathfrak{E}ncrypt$可以相同，也可以不同。若加密算法$Encrypt$和$\mathfrak{E}ncrypt$相同，则借助标准的key-switching技术，所生成的密文可再revert回基于初始密钥$s{k}_1$的密文。

6.2 Bootstrapping

对于$\mathbf{s}=(s_1,?,s_n)\in {\mathbb{B}}^n$。
对$\mu \in \mathcal{P}$的TWLE加密为：

• $\mathbf{c}\leftarrow TLW{E}_{\mathbf{s}}=(a_1,?,a_n,b)\in {\mathbb{T}}_q^{n+1}$

其中：

• $a_j\stackrel{\S }{\leftarrow }{\mathbb{T}}_q$
• $b={\sum }_{j=1}^n{s}_j?a_j+{\mu }^{?}$，${\mu }^{?}=\mu +e$，$e$为"small" noise error。

bootstrapping的目的是：

• 生成相同明文的TLWE密文，但具有减少的noise $e^{\prime }<e$。

目前为止，已知的对密文自举的方式，仅为Gentry的recryption技术。

在TFHE场景下，其包含2个步骤：

• 1）获取噪声明文${\mu }^{?}$为${\mu }^{?}=b?{\sum }_{j=1}^n{s}_j?a_j\in {\mathbb{T}}_q$。
  已知$s_j$的密文，该计算是线性的。
• 2）对${\mu }^{?}$四舍五入恢复到最近的明文$\mu$，具体为$\mu =\frac{?p{\mu }^{?}?\mathrm{mod}p}{p}\in \mathcal{P}$。

以上这2个步骤可基于已加密数据来操作。第一个步骤中，已知$s_j$的密文，该计算是线性的。第二个rounding四舍五入步骤，会更困难，可借助多项式来解决。

rounding with polynomials：
已知多项式$\mathfrak{v}=v_0+v_{1}X+?+v_{N?1}{X}^{N?1}\in {\mathbb{T}}_{N,p}[X]={\mathbb{T}}_p[X]/(X^N+1)$。其与单项式$X^{?j}$的外乘表示为：【见本论文3.3节】
$X^{?j}?\mathfrak{v}(X)=X^{2N?j}?\mathfrak{v}(X)=\{\begin{array}{cc}{v}_j+?& \text{for?}0\le j<N\\ ?v_j+?& \text{for?}N\le j<2N\end{array}$
即，当$0\le j<N$时，多项式$X^{?j}?\mathfrak{v}(X)$的常量项为$v_j$。利用可特点，可用于将torus元素${\mu }^{?}\in {\mathbb{T}}_q$ round 为 某元素$\mu \in {\mathbb{T}}_p$，其中$p|q$。

由于${\mu }^{?}\in {\mathbb{T}}_q$，可写成${\mu }^{?}={\bar{\mu }}^{?}/q$，其中${\bar{\mu }}^{?}:=?q{\mu }^{?}?\mathrm{mod}q$，其中$0\le {\bar{\mu }}^{?}<q$。假设有$N\ge q$，则有$0\le {\bar{\mu }}^{?}<N$。也即意味着，多项式$\mathfrak{v}$的系数个数，多于，${\bar{\mu }}^{?}$的可能取值个数。因此，对于任意的$0\le j<q$，应用$X^{?j}?\mathfrak{v}(X)$可生成$v_j+?$，从而选定$v_j$值。特别地，$X^{?j}?\mathfrak{v}(X)=v_j+?$关系中，若选择$v_j:=\frac{?(pj)/q?\mathrm{mod}p}{p}$，并取$j={\bar{\mu }}^{?}$，则有：
$X^{?{\bar{\mu }}^{?}}?\mathfrak{v}(X)=\frac{?(p{\bar{\mu }}^{?})/q?\mathrm{mod}p}{p}+?=\frac{?p{\mu }^{?}?\mathrm{mod}p}{p}+?=\mu +?$
这样，该多项式的常量项即为rounded值$\mu \in {\mathbb{T}}_p$。

举个例子：

6.2.1 blind rotation

令${\bar{\mu }}^{?}=?q{\mu }^{?}?\mathrm{mod}q$，同时令${\bar{a}}_j=?q{a}_j?\mathrm{mod}q$和${\bar{b}}_j=?q{b}_j?\mathrm{mod}q$。
为bootstrap，可将（无rounding）的decryption看成是：
$?{\bar{\mu }}^{?}=?\bar{b}+{\sum }_{j=1}^n{s}_j{\bar{a}}_j(\mathrm{mod}q)$
根据该值构建单项式$X^{?{\bar{\mu }}^{?}}$，对$X^{?{\bar{\mu }}^{?}}?\mathfrak{v}(X)$ evaluate可获得明文$\mu$。该思想的并发症在于其假设$q<N$，而实际设置中未验证该假设。经典密码学参数有： N ∈ { 2 10 , 2 11 , 2 12 } N\in\{2^{10},2^{11},2^{12}\} N∈{210,211,212}和 q ∈ { 2 32 , 2 64 } q\in\{2^{32},2^{64}\} q∈{232,264}：

• 1）首先，$X^{?{\bar{\mu }}^{?}}?\mathfrak{v}(X)$关系定义于模$X^N+1$，即意味着，与${\mathbb{Z}}_N[X]$元素相乘后，$x$的order为$X^{2N}$（即$X^{2N}=1$），从而$X^{?{\bar{\mu }}^{?}}?\mathfrak{v}(X)$中的指数$?{\bar{\mu }}^{?}$定义于模$2N$。${\bar{\mu }}^{?}$值需重新调整为模$2N$。
  对应的结果就是，并不再是依赖$?{\bar{\mu }}^{?}=?\bar{b}+{\sum }_{j=1}^n{s}_j{\bar{a}}_j(\mathrm{mod}q)$，而改为依赖近似值：
  $?{\tilde{\mu }}^{?}=?\tilde{b}+{\sum }_{j=1}^n{s}_j{\tilde{a}}_j(\mathrm{mod}2N)$
  其中：

  • $\tilde{b}=?2Nb?\mathrm{mod}2N$
  • ${\tilde{a}}_j=?2N{a}_j?\mathrm{mod}2N$

  该近似值可能会给噪声添加一个额外的small error。

  通过离散化模$2N$额外引入的error称为drift。可通过仔细选择参数来处理其对结果的影响。

• 2）由于多项式$\mathfrak{v}\in {\mathbb{T}}_{N,p}[X]$，因此其有$N$个系数，最多可为${\tilde{\mu }}^{?}$编码$N$个值。具体解决方案为：确保${\tilde{\mu }}^{?}$的最高有效位为0。这样，${\tilde{\mu }}^{?}$就最多有$N$个可能值。

基于以上考虑，定义test多项式$\mathfrak{v}$为：
$\mathfrak{v}:=\mathfrak{v}(X)={\sum }_{j=0}^{N?1}{v}_j{X}^j)$
其中$v_j=\frac{?\frac{pj}{2N}?\mathrm{mod}p}{p}\in \mathcal{P}$

若该drift is contained，且$0\le ({\tilde{\mu }}^{?}\mathrm{mod}2N)<N$，则relation：
$X^{?\tilde{b}+{\sum }_{j=1}^n{s}_j{\tilde{a}}_j}?\mathfrak{v}(X)=X^{?{\tilde{\mu }}^{?}}?\mathfrak{v}(X)=\mu +?$
成立。

更具体来说，令${\mathfrak{q}}_j=X^{?\tilde{b}+{\sum }_{i=1}^j{s}_i{\tilde{a}}_i}?\mathfrak{v}$，则该外乘具有同态性：

从而提供了基于${\mathfrak{q}}_0=X^{?\tilde{b}}?\mathfrak{v}$，$j$由1到$n$，迭代计算${\mathfrak{q}}_n=X^{?\tilde{b}+{\sum }_{i=1}^n{s}_i{\tilde{a}}_i}?\mathfrak{v}$的方法。

Gentry的recrption类似，但基于的是已加密数据，由于rounding方法中包含了多项式，需依赖TGLWE加密方案。

6.2.2 Sample extraction

上一节的转换步骤，可将明文$\mu \in \mathcal{P}$的TLWE密文，转换为，常量项为$\mu$的多项式明文$\mu (X):=X^{?{\tilde{\mu }}^{?}}?\mathfrak{v}\in {\mathcal{P}}_N[X]$ 的TGLWE密文。基于不同的key，通过$\mu$的refreshed TLWE加密，可提取该常量项。该过程称为sample extraction。

需注意，尽管其用于常量项，该技术也可调整为用于提取$\mu$的其它元素。

6.2.3 Key switching

至此，几乎快实现整个流程了。

以上流程中，密文$\mathbf{c}$和${\mathbf{c}}^{\prime }\leftarrow SampleExtract(BlindRotat{e}_{bsk}(\mathfrak{c},\tilde{\mathfrak{c}}))$，均为明文$\mu$的加密，但其使用不同的参数集合：
$\mathbf{c}\leftarrow TLW{E}_s(\mu )\in {\mathbb{T}}_q^{n+1}$
${\mathbf{c}}^{\prime }\leftarrow TLW{E}_{s^{\prime }}(\mu )\in {\mathbb{T}}_q^{kN+1}$

key switching算法用于，将某key下的密文，转换为，另一key下的密文。其实现需要key-switching keys，即会对，对应原始key $s$的key $s^{\prime }$的bits，做TLWE加密。该流程理论上看起来与bootstrapping类似，但二者的本质区别在于：

• bootstrapping用于降低噪声，且计算要求高
• key switching用于增加噪声，但evaluate更便宜。

6.2.4 Putting it all together

完整的bootstrapping流程为：

6.3 Programmable Bootstrapping

（常规的）bootstrapping本质上依赖于：

• 对于任意的$0\le j<N$，有$X^{?j}?\mathfrak{v}(X)=v_j+?$

以上各章节中，test多项式$\mathfrak{v}\in {\mathbb{T}}_N[X]$定义为：
$\mathfrak{v}(X)={\sum }_{j=0}^{N?1}\frac{?pj/(2N)?\mathrm{mod}p}{p}{X}^j$

现在，已知函数$f:{\mathbb{T}}_p\to {\mathbb{T}}_p$，定义test多项式$\mathfrak{v}$为：
$\mathfrak{v}(X)={\sum }_{j=0}^{N?1}f(\frac{?pj/(2N)?\mathrm{mod}p}{p})X^j$

注意，该resulting多项式$X^{?{\tilde{\mu }}^{?}}?\mathfrak{v}(X)$，假设drift的影响可忽略，且$0\le ({\tilde{\mu }}^{?}\mathrm{mod}2N)<N$，其具有常量项：
$f(\frac{?p{\tilde{\mu }}^{?}/(2N)?\mathrm{mod}p}{p})=f(\mu )$

因此，对于上一节的bootstrapping流程，其输入为某（noisy）密文$\mathbf{c}\leftarrow TLW{E}_s(\mu )$，输出为TLWE密文${\mathbf{c}}^{\prime }\leftarrow TLW{E}_s(f(\mu ))$，其中引入了少量噪声。
注意，该常规bootstrapping对应$f$的identity function。

同时注意：当函数$f$为negacyclic（即，若$f(\mu +\frac{1}{2})=?f(\mu ),?\mu \in {\mathbb{T}}_p$），可解除对${\tilde{\mu }}^{?}$的范围限制。基于torus的“sign”函数，即为一种negacyclic函数。

6.4 更多技术

上面的bootstrapping和programmable bootstrapping技术，可在不同方向进行扩展，如：

• 任意函数：
  

• 更大精度：
  

• multi-value programmable bootstrapping：
  

• Ternary keys and more：
  

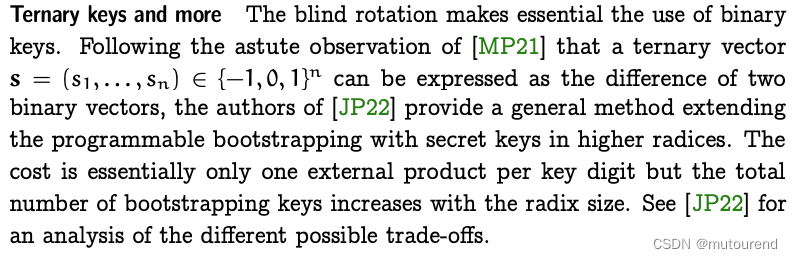
参考资料

[1] Zama团队的Marc Joye 2021年论文 Guide to Fully Homomorphic Encryption over the [Discretized] Torus

FHE系列博客

• 技术探秘：在RISC Zero中验证FHE——由隐藏到证明：FHE验证的ZK路径（1）
• 基于[Discretized] Torus的全同态加密指引（1）