基础算法(8):高精度加减乘除
发布时间:2024年01月02日
目录
? ? ?为什么要有这么一种算法?因为当我们想需要对两个很大的数进行运算,比如38149194919814894819+89198481314819,结果很显然超出了int范围能表示的整数,我们这时候就要用到高精度算法,高精度算法通过用数组来存储数字的每一位,然后进行运算进位,最后通过数组来输出结果
1.高精度加法
模板:
// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{
vector<int> C;
int t = 0;
for (int i = 0; i < A.size()||i < B.size(); i ++ )//判断A和B的大小
{
if (i < A.size()) t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if (t) C.push_back(t);
return C;
}
例题:
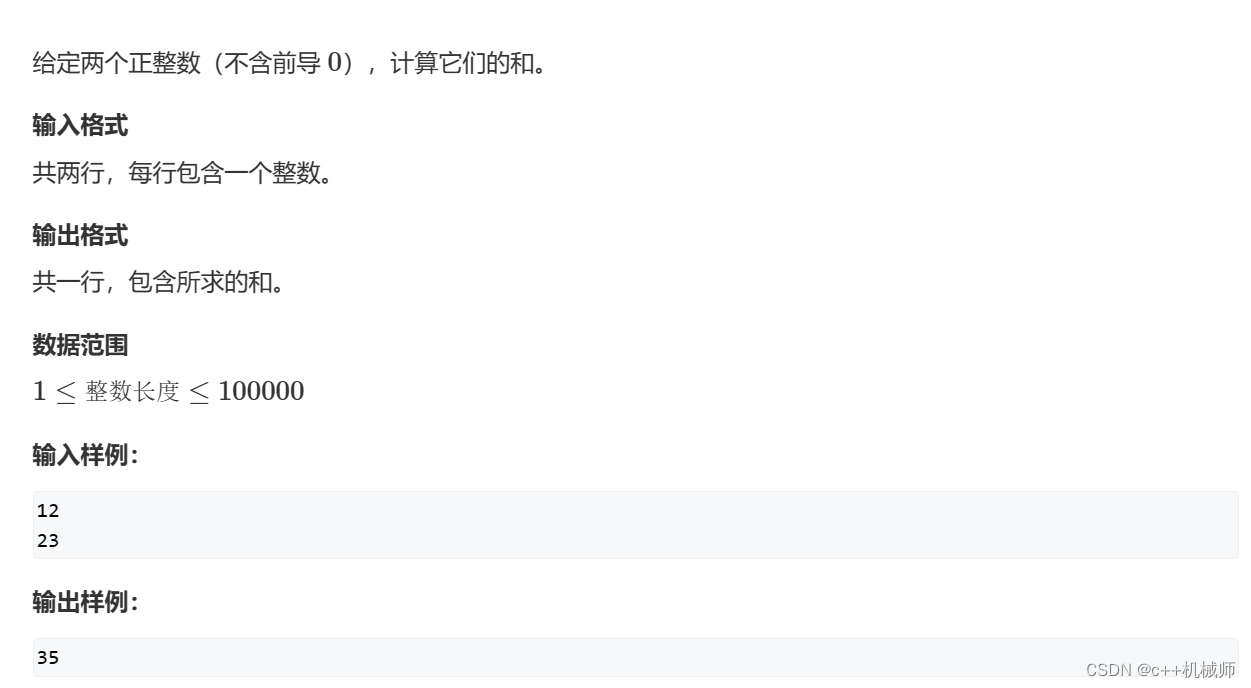 2
2
#include<iostream>
#include<vector>
using namespace std;
vector<int> add(vector<int> &A,vector<int> &B)
{
vector<int>C;
int t=0;
for(int i=0;i<A.size()||i<B.size();i++)
{
if(i<A.size())t+=A[i];
if(i<B.size())t+=B[i];
C.push_back(t%10);
t/=10;
}
if(t)C.push_back(1);
return C;
}
int main()
{
string a,b;
vector<int>A,B;
cin>>a>>b;
for(int i=a.size()-1;i>=0;i--)A.push_back(a[i]-'0');//我们将个位数存到第一个元素,这样可以更好的在最后补位,因为在数组末尾添加元素是比较容易的
for(int i=b.size()-1;i>=0;i--)B.push_back(b[i]-'0');
auto C=add(A,B);
for(int i=C.size()-1;i>=0;i--)printf("%d",C[i]);//因为是逆序存储,输出的的时候也要从最后开始输出
return 0;
}2.高精度减法
模板:
//C=A-B 且A>B
vector<int> sub(vector<int>& A,vector<int>& B)
{
vector<int> C;
for(int i=0,t=0;i<A.size();i++)
{
//每次循环进行A[i]-B[i]-t运算
t=A[i]-t;//减去上次运算借的位,没有借位就减去0,借位就减去1
if(i<B.size())t-=B[i];//判断B[i]是否存在,如果存在,上一步算完A[i]减去进位的值
//等于t,t=t-B[i],算的就是该位两数相减的值
C.push_back((t+10)%10);//有两种情况,一种算完t<0,这时候向前借一位,即t+10,就是这一位的值;还有一种是t>0,为了减少代码,我们也+10再%10,就抵消了
if(t<0)t=1;//t<10.说明借位了,t=1
else t=0;//t?10.不用借位,t=0
}
while(C.size()>1&&C.back()==0)C.pop_back();//去除前导0
return C;
}? ? ? ?减去上次运算借的位,没有借位就减去0,借位就减去1
? ? ? ?接下来判断B[i]是否存在,如果存在,上一步算完A[i]减去进位的值等于t,t=t-B[i],算的就是该位两数相减的值
? ? ? ?C.push_back((t+10)%10)有两种情况,一种算完t<0,这时候向前借一位,即t+10,就是这一位的值;还有一种是t>0,为了减少代码,我们也+10再%10,就抵消了。
? ? ? 最后如果t<0,说明借位了,t=1;否则没借位,t=0。
例题:

#include<iostream>
#include<vector>
using namespace std;
//判断是否有A>B
bool cmp(vector<int>& A,vector<int>& B)
{
if(A.size()!=B.size())return A.size()>B.size();
for(int i=A.size()-1;i>=0;i--)
if(A[i]!=B[i])
return A[i]>B[i];
return true;
}
//C=A-B 且A>B
vector<int> sub(vector<int>& A,vector<int>& B)
{
vector<int> C;
for(int i=0,t=0;i<A.size();i++)
{
//每次循环进行A[i]-B[i]-t运算
t=A[i]-t;//减去上次运算借的位,没有借位就减去0,借位就减去1
if(i<B.size())t-=B[i];//判断B[i]是否存在,如果存在,上一步算完A[i]减去进位的值
//等于t,t=t-B[i],算的就是该位两数相减的值
C.push_back((t+10)%10);//有两种情况,一种算完t<0,这时候向前借一位,即t+10,就是这一位的值;还有一种是t>0,为了减少代码,我们也+10再%10,就抵消了
if(t<0)t=1;//t<10.说明借位了,t=1
else t=0;//t?10.不用借位,t=0
}
while(C.size()>1&&C.back()==0)C.pop_back();//去除前导0
return C;
}
int main()
{
string a,b;
vector<int>A,B;
cin>>a>>b;
for(int i=a.size()-1;i>=0;i--)A.push_back(a[i]-'0');
for(int i=b.size()-1;i>=0;i--)B.push_back(b[i]-'0');
if(cmp(A,B))
{
auto C=sub(A,B);
for(int i=C.size()-1;i>=0;i--)printf("%d",C[i]);
}
else
{
auto C=sub(B,A);
printf("-");
for(int i=C.size()-1;i>=0;i--)printf("%d",C[i]);
}
return 0;
}? ? ?我们首先要判断A和B的大小,要用大的减去小的,如果A<B,那我们用B-A,输出时候加上负号即可,判断完之后就是套模板了,最后逆序输出。
3.高精度乘法
模板:
//大数乘小数 高精度乘低精度
vector<int> mul(vector<int>& A,int b)
{
vector<int>C;
int t=0;
for(int i=0;i<A.size()||t;i++)//如果i>=A.size()且t!=0,就要处理剩余的t,也就是最后一次进位
{
if(i<A.size())t+=A[i]*b;//判断A是否已经乘完
C.push_back(t%10);
t/=10;
}
return C;
}例题:

#include<iostream>
#include<vector>
using namespace std;
//大数乘小数 高精度乘低精度
vector<int> mul(vector<int>& A,int b)
{
vector<int>C;
int t=0;
for(int i=0;i<A.size()||t;i++)//如果i>=A.size()且t!=0,就要处理剩余的t,也就是最后一次进位
{
if(i<A.size())t+=A[i]*b;//判断A是否已经乘完
C.push_back(t%10);
t/=10;
}
return C;
}
int main()
{
string a;
int b;
cin>>a>>b;
vector<int>A;
for(int i=a.size()-1;i>=0;i--)A.push_back(a[i]-'0');
auto C=mul(A,b);
for(int i=C.size()-1;i>=0;i--)printf("%d",C[i]);
return 0;
}4.高精度除法
模板:
//A/b,商是C,余数是r
vector<int> div(vector<int>& A,int b,int &r)
{
vector<int>C;
for(int i=A.size()-1;i>=0;i--)
{
r=r*10+A[i];//算余数
C.push_back(r/b);//商
r%=b;//对除数取模进行下一步算余数的运算
}
reverse(C.begin(),C.end());
while(C.size()>1&&C.back()==0)C.pop_back();
return C;
}
例题:

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
//A/b,商是C,余数是r
vector<int> div(vector<int>& A,int b,int &r)
{
vector<int>C;
for(int i=A.size()-1;i>=0;i--)
{
r=r*10+A[i];//算余数
C.push_back(r/b);//商
r%=b;//对除数取模进行下一步算余数的运算
}
reverse(C.begin(),C.end());
while(C.size()>1&&C.back()==0)C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin>>a>>b;
vector<int>A;
for(int i=a.size()-1;i>=0;i--)A.push_back(a[i]-'0');
int r;
auto C=div(A,b,r);
for(int i=C.size()-1;i>=0;i--)printf("%d",C[i]);
cout<<endl<<r<<endl;
return 0;
}
文章来源:https://blog.csdn.net/pancodearea/article/details/135339882
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- RocketMQ实战-win10系统安装RocketMQ
- Web Vitals
- 树莓派4B ubuntu系统换源 ign解决办法
- 基于SpringBoot的图书管理系统
- 【国产之光】开年尝鲜——优秀的AI编码助手 Fitten Code
- SpringBoot自动配置原理
- Pyside6/PyQt如何添加右键菜单选项的勾选状态
- 消息队列选型:Kafka 如何实现高性能?
- 【C语言】TCP测速程序
- 集群部署篇--Redis 集群动态伸缩