机器学习 (第9章 概率图模型)

一、学习目标

1.学习概率图模型中两种重要的模型：贝叶斯网络和马尔科夫随机场

2.学习使用概率图模型去进行实际问题的学习与推断

3.学习近似推断

二、贝叶斯网络

????????概率图模型基于图，而图这种数据结果分为两种：有向图和无向图，针对有向（无环）图结构，实现的是贝叶斯网络，针对无向图，则为马尔可夫随机场。

1.有向无环图

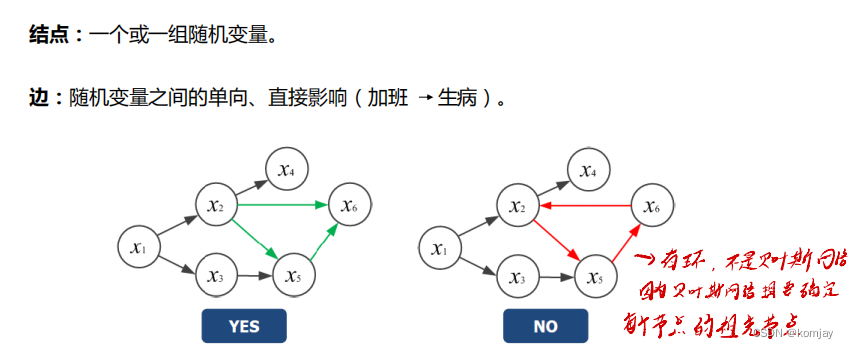
????????根据图中每个结点不同，可提取出不同的相关结点，如以x3为例

2.联合概率分布

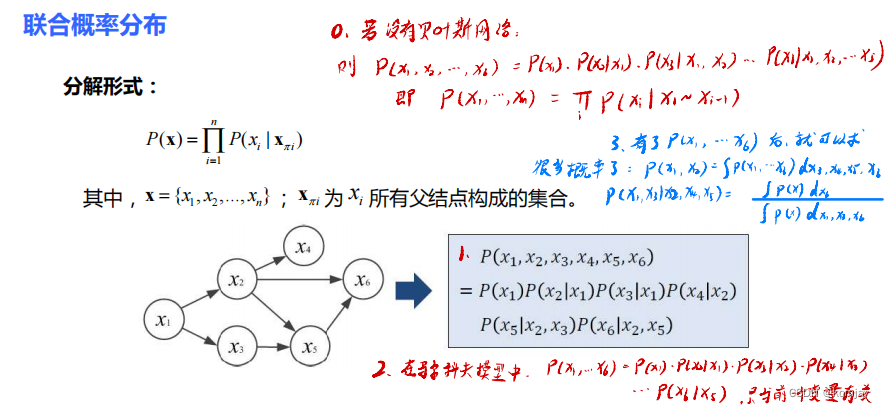
? ? ? ? 我们之所以搞出这么一个图，最终目的是想求解出所有x同时发生的概率，即联合概率，因为有了联合概率分布，我们就可以随意求解其他情况的概率，如下图中3.所写。

????????在贝叶斯网络，其联合概率计算是由图来定义的，如下图1.所展示，而如果没有贝叶斯网络，我们无法了解各个变量之间是否有联系，就认为都有联系，于是列出的联合概率公式为0.所示

。可以发现，贝叶斯网络的作用就是消除了部分变量之间的联系，或者说得到了某些变量之间存在独立性，从而方便联合概率的计算。

? ? ? ? 以一个例子来看看贝叶斯网络的运用：

? ? ? ? 显然，第一题是比较简单的，直接查表计算就行：

? ? ? ? 而如果要计算条件概率，就会稍微麻烦：（特别是缺少某一个变量时，我们需要用积分法消去这个变量）

3.条件独立性

? ? ? ? 对于一个很大的贝叶斯网络，我们需要有一个很高效的方法的快速辨别两个变量之间是不是独立的，但我们这里考虑条件独立性，条件独立性不同于独立性，条件独立性，必须要在某一条件下，考虑另外两个变量之间的独立性。三个重要准则如下：

? ? ? ? 例如以t2t，可以进行证明：

? ? ? ? 而如果抛去C的条件，考虑A和B之间的独立性，则A不与B独立：（实例化证明不是什么高大上的方法，就是高中数学求选项错误的方法）

? ? ? ? 知道上面的三个情况后，就可以判别网络上各个点的条件独立性，其原理为全局马尔科夫性：

? ? ? ? 以例子来说明：

? ? ? ? 再讲一个反例：

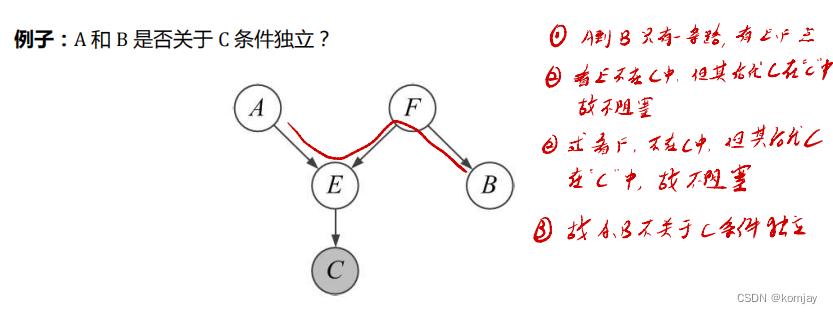
? ? ? ? 除此之外，我们还有另外两条规则来判断独立性，是为局部马尔科夫性，是全局马尔科夫性的一些特例，但相比于上面，更常用：

二、马尔科夫随机场

? ? ? ? 马尔科夫随机场是针对无向图结构的一种技术，由于缺少有向无环图的上下级关系，无法像贝叶斯一样可以列出各变量之间的联系，于是其引入团和极大团的概念：

? ? ? ? 在马尔科夫随机场中，既然无法确定结点之间的关系，那就认为两点有连线就有联系，是相互影响的关系。为了计算所有变量的联合概率，那就变成计算所有团（或者极大团）的概率。于是引入势函数来计算团内部变量之间的相关性（相当于贝叶斯网络中计算联合概率分布中的条件概率）：

? ? ? ? 以一个例子来看这条公式：（使用了极大团）

? ? ? ? 而马尔科夫随机场一个伟大的应用是受限玻尔兹曼机，其结构和相关定义如下：

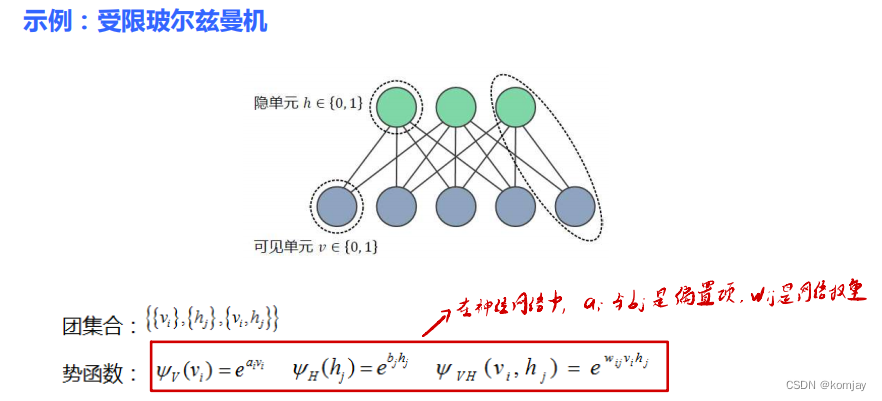
? ? ? ? 如上面所写，受限玻尔兹曼机实际上就相当于一层神经网络，只是受限玻尔兹曼机是从马尔科夫随机场的角度得到的结果，而神经网络是从感知机的角度得到的。受限玻尔兹曼机的过程实际上也跟神经网络一致，也是前向计算出概率，再误差反向传回，修改参数。最后可以得到其联合概率值：

? ? ? ? 通过受限玻尔兹曼机无法直接得到联合概率分布，而根据我们使用神经网络的习惯，我们也确实不用得到联合概率分布，只要得到具体的v的概率是多少就行，而非要得到联合概率分布，也只能不断采点来得到。

2.条件独立性

? ? ? ? 马尔可夫随机场也有其对应的条件独立性，首先是全局马尔可夫性，比贝叶斯的简单，看图就懂：

? ? ? ? 还有局部马尔可夫性和成对马尔可夫性：

四、学习与推断

?五、近似推断