控制第八章 非线性系统【自用/最新】
目录标题
Q 非线性部分指的是输入、控制器、执行器、还是输出?
指的是:在进行一系列等效后,将系统分为 单位负反馈 下 非线性部分与线性部分串联 的结构中,非线性部分前的输入
- 这种等效需要最左边输入r=0
- 这种等效后的输出可能与原输出不一致了
Q 非线性的表达式怎么与传递函数对应?
比如:
x
¨
+
x
˙
+
x
=
0
\ddot x + \dot x + x=0
x¨+x˙+x=0对应的传递函数是什么样的?
回答:
这是一种数学思想,其意思为x存在一个微小变化
Δ
x
\Delta x
Δx时,
x
¨
\ddot x
x¨ 变为
Δ
x
¨
\Delta\ddot x
Δx¨,
x
˙
\dot x
x˙变为
Δ
x
˙
\Delta \dot x
Δx˙,常数项变为0。
然后列出特征方程
Q 什么叫“平衡点”,是稳定的点/最终收敛到的点吗
并不是 平衡点指的是
x
¨
\ddot x
x¨和
x
˙
\dot x
x˙均为0的点,这些点处的x不动。
对于线性定常系统,原点是唯一平衡点
K 非线性系统不满足叠加性
相平面法
基本概念
相轨迹
相平面上的轨迹叫做相轨迹
相轨迹横坐标是
x
x
x,纵坐标是
x
˙
\dot x
x˙,斜率是
d
x
˙
d
x
\frac{d\dot x}{dx}
dxdx˙?【后面等倾斜线法有用】

相轨迹的运动方向
上半平面
x
˙
>
0
\dot x > 0
x˙>0:向右移动
下半平面
x
˙
<
0
\dot x < 0
x˙<0:向左移动
相平面的平衡点(奇点)
x
¨
\ddot x
x¨和
x
˙
\dot x
x˙均为0的点
对于线性定常系统,原点是唯一平衡点
特征方程
指求出平衡点后,一个平衡点对应一个方程。
特征方程的定义笔者比较模糊,但是大致意思是:在平衡点附近,一个微小增量的表达式。
见下图两个例子
Δ x ˙ 2 \Delta \dot x^2 Δx˙2的部分省略了,因为他是 Δ x \Delta x Δx的高阶无穷小。
?
等价无穷小之间,可以进行替换
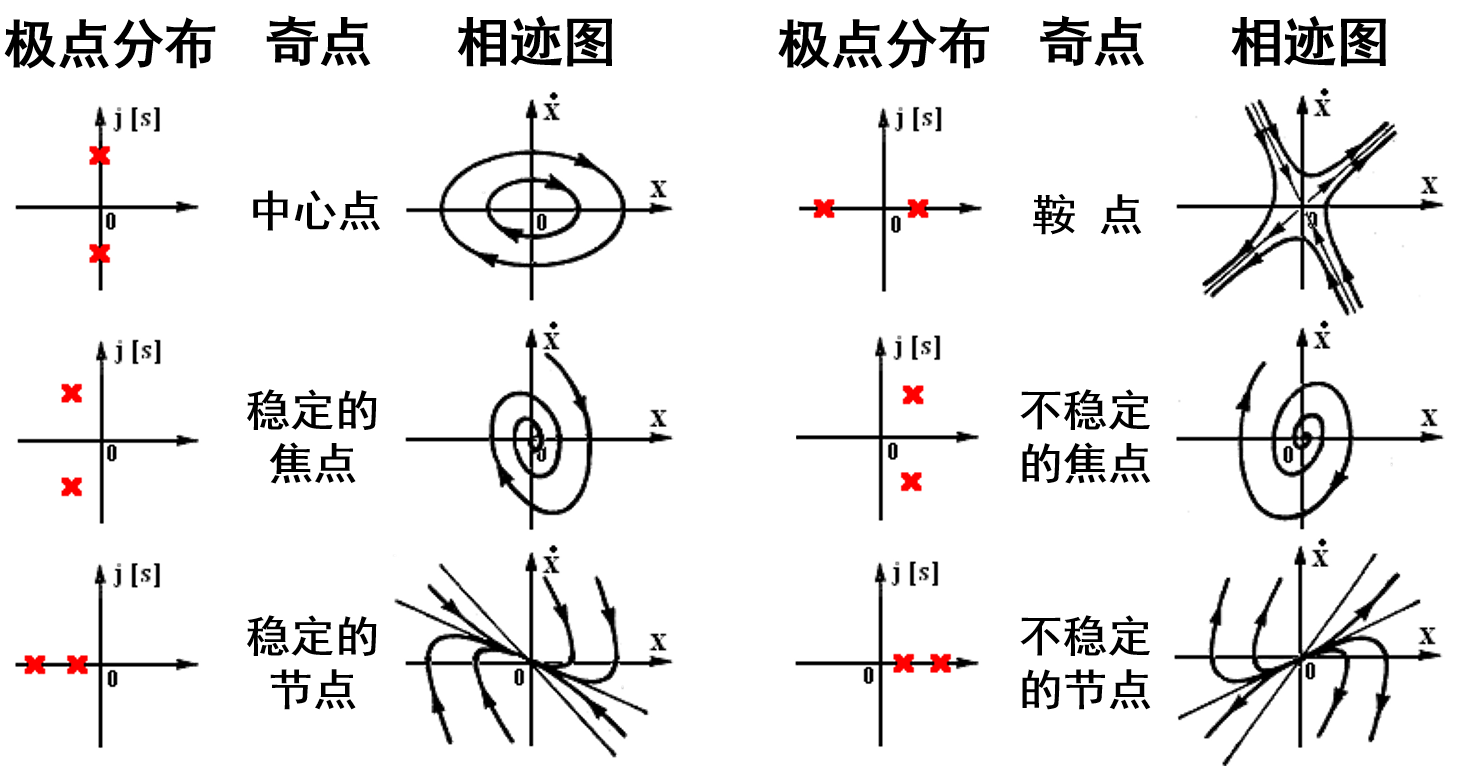
特征方程式根对应图像
根据特征方程式的根分布情况,共有六种相轨迹
等倾斜线法
等倾斜线法思路
做出一系列相轨迹斜率为常数的曲线,目的是求出斜率
x
¨
=
d
x
˙
d
x
d
x
d
t
=
x
˙
d
x
˙
d
x
=
?
f
(
x
,
x
˙
)
α
=
d
x
˙
d
x
=
?
f
(
x
,
x
˙
)
x
˙
\begin{aligned} \ddot{x} & =\frac{d \dot{x}}{d x} \frac{d x}{d t}=\dot{x} \frac{d \dot{x}}{d x}=-f(x, \dot{x}) \\ \alpha & = \frac{d\dot x}{dx}=\frac{-f(x, \dot{x})}{\dot{x}} \end{aligned}
x¨α?=dxdx˙?dtdx?=x˙dxdx˙?=?f(x,x˙)=dxdx˙?=x˙?f(x,x˙)??
思路:
- 把 α \alpha α看作常数,记录一系列 α \alpha α对应的斜率
- 相轨迹穿过该线时的斜率为已知
相平面-强化【20231102】
相轨迹绘制专类
Q 绘制相轨迹,何时根据渐近线,何时根据奇点
假设相轨迹方程如下式: e ¨ + a e ˙ + b e = c \ddot e + a\dot e + be=c e¨+ae˙+be=c
A1 当e前系数b不为零时,用奇点判断
a≠0 b≠0 c任意时, 写特征方程判断奇点类型
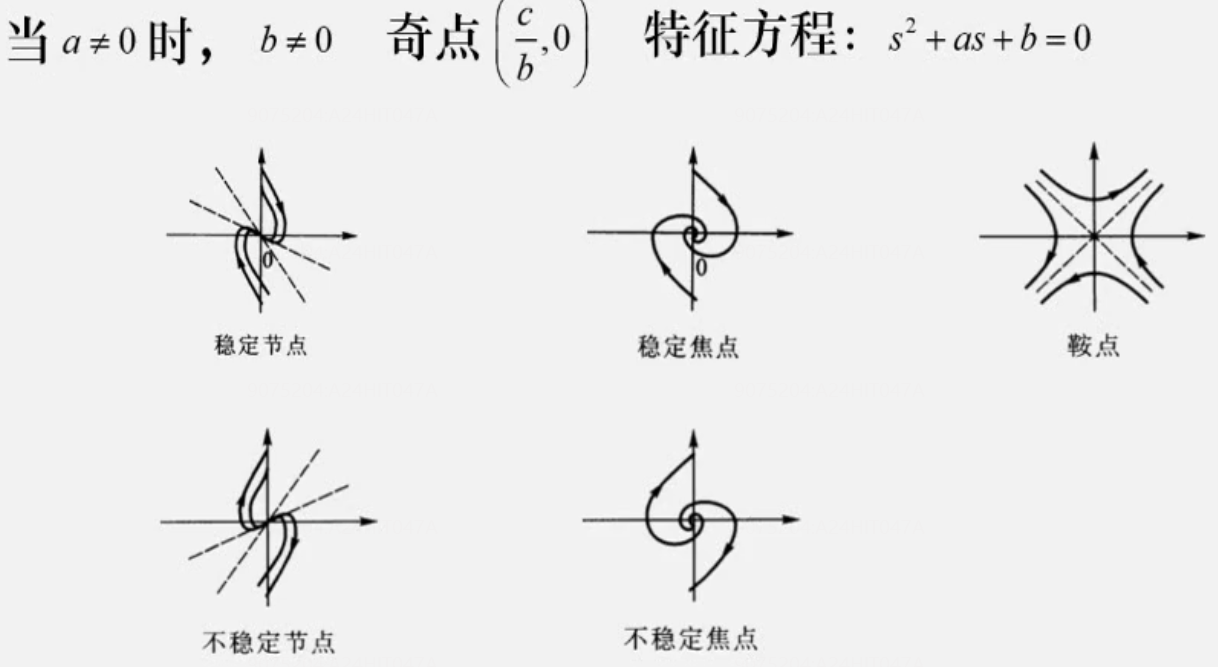
a=0 b≠0 c任意时,奇点为中心点或者鞍点
此处只列举了中心点的情况,挺笨的没什么好说
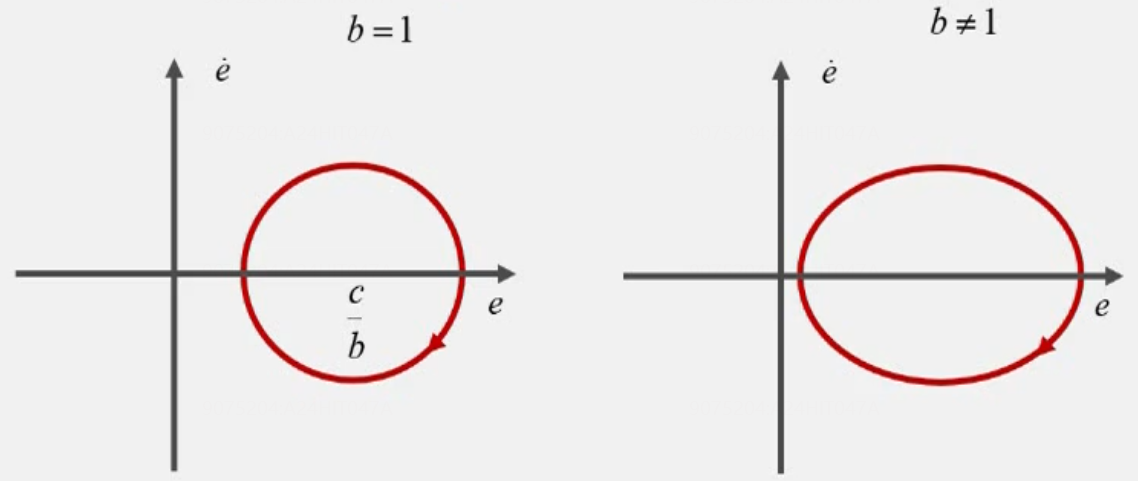
【?具体的图像需要,等倾斜线法?】
A2 当e前系数b为零
a≠0 b=0 c≠0,水平渐近线
此时
e
¨
+
a
e
˙
=
c
\ddot e + a\dot e =c
e¨+ae˙=c,可以求出
e
˙
=
c
a
\dot e = \frac{c}{a}
e˙=ac?【可以简单记为:去掉
e
¨
\ddot e
e¨后求解】
此时系统中所有相轨迹都趋向于该水平渐近线

a=0 b=0 c=0, 相轨迹为某条平行横轴直线
a=0 b=0 c≠0,相轨迹为抛物线
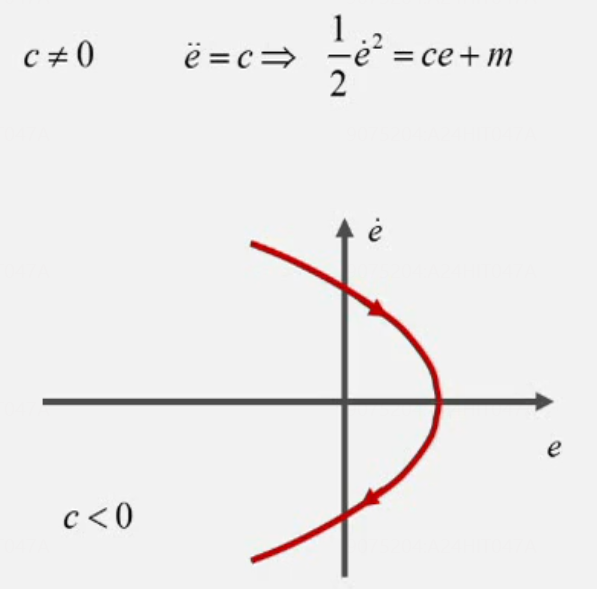
a≠0 b=0 c=0,相轨迹为一群斜率相等的直线

什么时候根据奇点类型判断、什么时候根据渐近线判断?
答:当e前的系数不等于0时,求出奇点类型进行判断,等于0时,判断是直线/渐近线/抛物线
【个人感觉
a
≠
0
,
b
=
0
,
c
≠
0
a \neq 0, b = 0, c \neq 0
a=0,b=0,c=0】是最恶心的
Q 怎么求奇点,奇点/稳定点/特征方程特征根区别
特征方程是针对不同奇点展开的,是用来判断奇点的性质的
奇点:令各阶导函数为零、求出来的点
特征方程:在各个奇点处的方程
Q 求奇点
解析函数求偏导
最后的线性化方程中,一阶导前的系数是非线性方程对一阶导数求偏导;
最后的线性化方程中,变量前的系数是非线性方程对变量求偏导
小误差🌟🌟
令
x
1
=
x
e
1
+
Δ
x
x_1=x_{e1}+\Delta x
x1?=xe1?+Δx,其中
x
e
1
x_{e1}
xe1?是奇点的横坐标;
对于该式求导,最终可以将非线性系统化简成关于
Δ
x
(
Δ
x
˙
,
Δ
x
¨
)
\Delta x(\Delta \dot x, \Delta \ddot x)
Δx(Δx˙,Δx¨)的微分方程,根据该式,列写特征方程从而判断奇点类型
注意:
(
Δ
x
)
2
(\Delta x)^2
(Δx)2是
Δ
x
\Delta x
Δx的高阶无穷小,可以直接令其等于零

举例
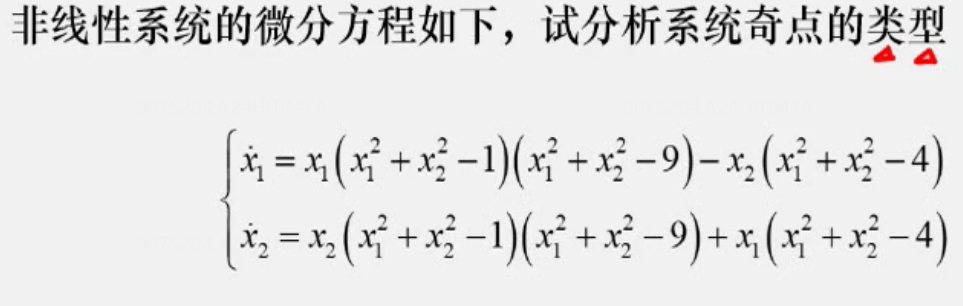

Q 各种不同奇点图像类型汇总🌟
稳定焦点-具有负实部的共轭复根-向心螺旋线
类似欠阻尼
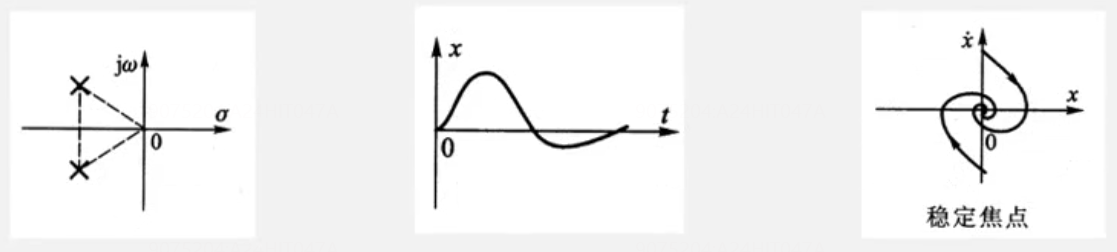
稳定节点-两负实根-两个渐近线
类似过阻尼
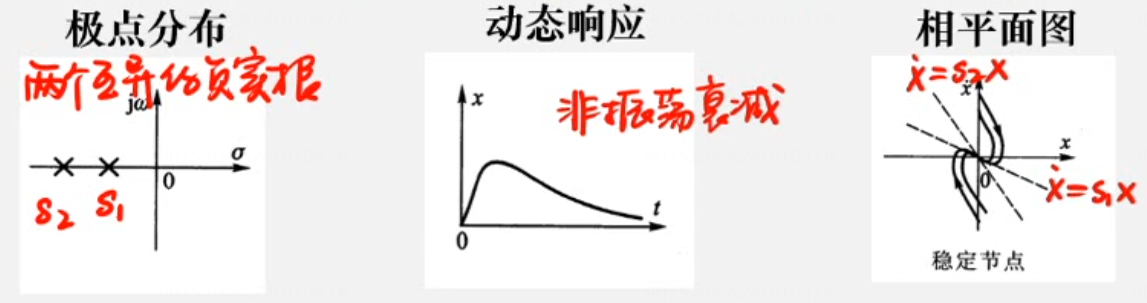
中心点-一对纯虚根-圆或椭圆
类似等幅振荡
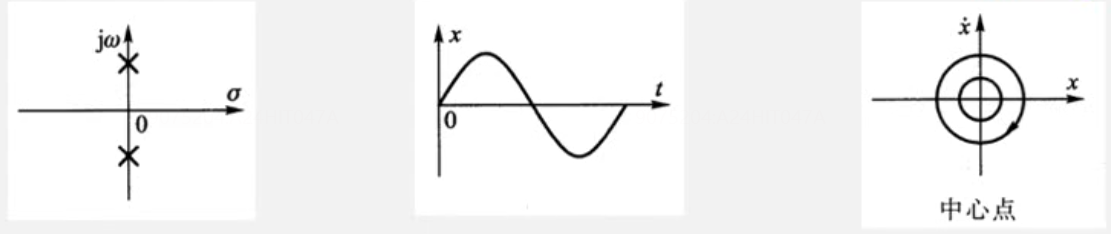
鞍点-一正一负纯实根-非震荡发散
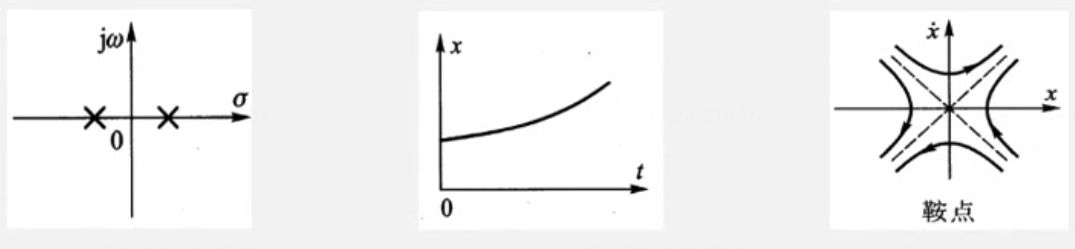
Q 等倾斜线法的原理,及何时使用此方法
使用条件:??
e ¨ + a e ˙ = c ( a ≠ 0 , c ≠ 0 ) \ddot e + a\dot e =c (a \neq 0, c \neq 0) e¨+ae˙=c(a=0,c=0)
原理:设相平面斜率为某个常值
将 α = d e ˙ d e \alpha = \frac{d\dot e}{de} α=dede˙?的值固定下来,则上式化为 α e ˙ + a e ˙ = c \alpha \dot e + a \dot e = c αe˙+ae˙=c
重要原则🌟
高等数学知识-求解微分方程
e ¨ = e ˙ d e ˙ d e \ddot e = \dot e \frac{d\dot e}{de} e¨=e˙dede˙?
相轨迹方向问题
当
e
˙
>
0
\dot e>0
e˙>0时,e增加,方向向右
当
e
˙
<
0
\dot e<0
e˙<0时,e减小,方向向左
相轨迹必将垂直穿过横轴处【斜率为无穷大】
微分方程大分类
见上述问题"Q 绘制相轨迹"
解题思路
- 写出分区微分方程,写出开关线
- 分区域讨论微分方程
- 画图
补充:相轨迹时间计算🌟
积分法
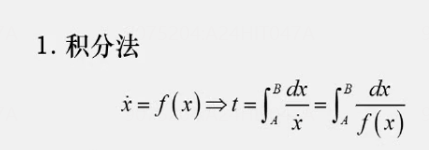
A,B是起点、终点的横坐标
注意:跨过
e
˙
=
0
\dot e=0
e˙=0的线上下两端表达式可能不一样
举例1 计算时间
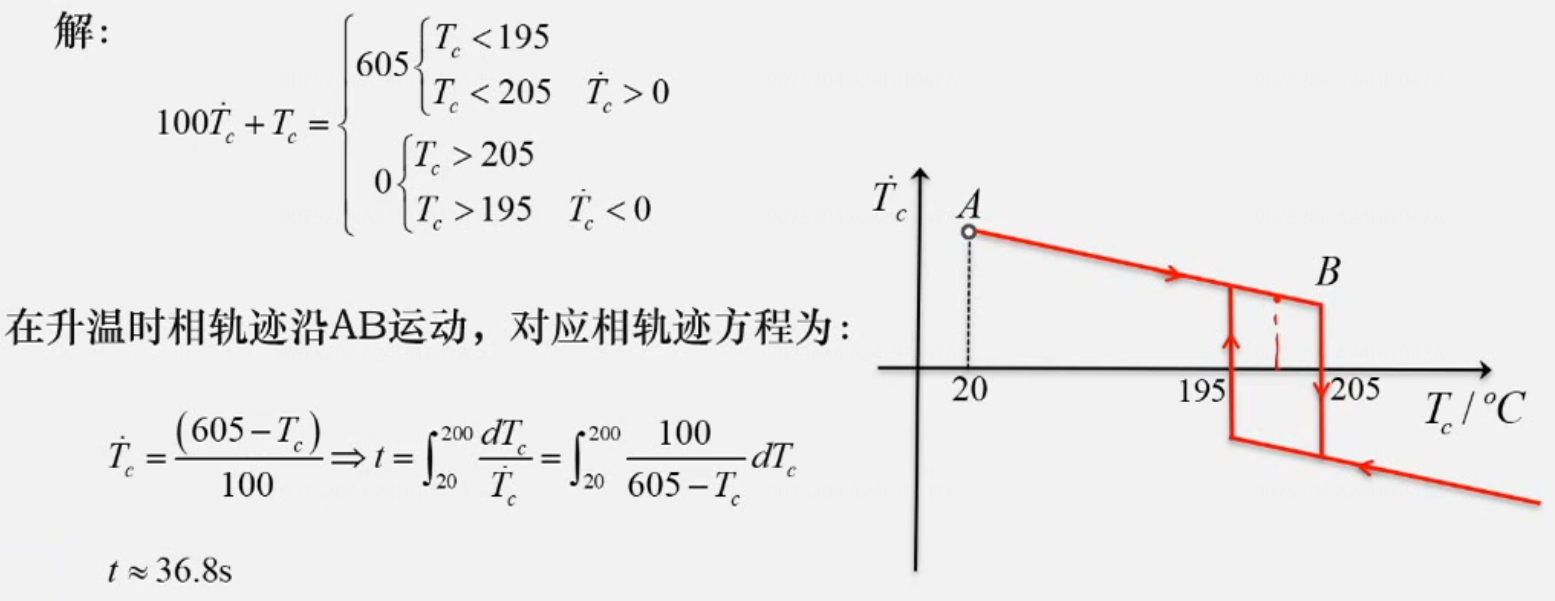
描述函数法【20231103】
Q N(A)的定义是什么
N(A)称为描述函数,是正弦输入信号作用下,非线性系统稳态输出中,一次谐波分量和输入信号的复数比。
A对应的幅值,是输入(传向非线性环节的信号)
x
(
t
)
x(t)
x(t)的对应幅值

因此,若要使用描述函数法,需要具备以下两个条件:①可化为非线性环节与线性环节的串联②非线性部分具有奇对称性
为了让描述函数法更好的工作,_______还应该满足以下性质
①低通滤波性②输入可以由一次谐波分量进行近似
Q* 为什么不考虑 ω \omega ω
描述函数一般为输入信号振幅 A A A的函数、当非线性环节中包含储能元件时,描述函数才同时为输入信号振幅 A A A和频率 ω \omega ω的函数,此时记为 N ( A , ω ) N(A, \omega) N(A,ω)【考研不涉及此情况】
Q* “输入为正弦”指的是等效非线性环节前的信号还是系统的输入?
是等效非线性环节【即 N ( A ) N(A) N(A)】前的信号,往往
Q* 为什么描述函数法中不考虑输入
因为描述函数法中假设了输入为0,A是在非线性系统前的正弦信号幅值
另外,在描述函数法中,系统输入r(t)=0
Q 当我们描述“存在自激振荡”时,非稳定点A0的其他点A是否会趋近于A0?
问题在于,幅值A是不断进行着周期运动,还是收敛于稳定点A0呢?
直接给出答案,是收敛于A0的;
不然A也太难看了,自己本身是正弦的幅值,自己还在周期运动
Q 如何理解描述函数法
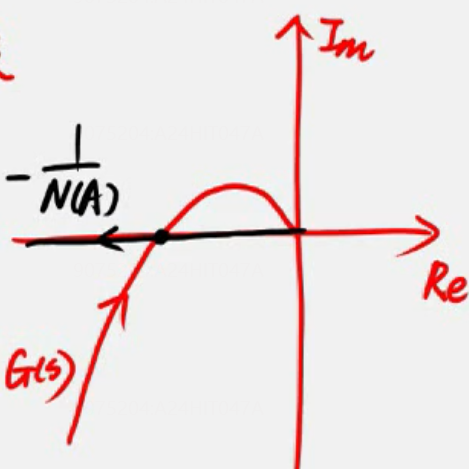
1 + N ( A ) G ( s ) = 0 ? G ( s ) = ? 1 N ( A ) 1+N(A) G(s)=0 \Rightarrow G(s)=-\frac{1}{N(A)} 1+N(A)G(s)=0?G(s)=?N(A)1?
-
相当于绘制了“广义奈奎斯特曲线”,该坐标轴下的(-1,j0)点实际上在变化;
实际上,原来的(-1,j0)点现在变成了(- 1 N ( A ) \frac{1}{N(A)} N(A)1?,j0)
描述函数求的是G(s=j ω \omega ω)(奈奎斯特曲线)与实轴交点和点(- 1 N ( A ) \frac{1}{N(A)} N(A)1?,j0)的关系
这个关系往往列出两个等式【实轴、虚轴】,从而得到 A A A和 ω \omega ω -
要理解“稳定”的含义:
有变小的趋势叫稳定
有变大的趋势叫不稳定
因此不稳定向稳定走才是稳定点 -
有交点,表明存在极限环,但是需要另外分析极限环的稳定性
重要公式
一类经典奈奎斯特曲线及特殊点
G
(
s
)
=
k
s
(
T
1
s
+
1
)
(
T
2
s
+
1
)
与实轴交点处:
ω
x
=
1
T
1
?
T
2
R
e
=
?
k
T
1
?
T
2
T
1
+
T
2
?渐近线:?
?
k
(
T
1
+
T
2
)
【可以不求】
\begin{array}{l} G(s)=\frac{k}{s\left(T_{1} s+1\right)\left(T_{2} s+1\right)} \\\\ 与实轴交点处:\\\\ \omega_{x}=\frac{1}{\sqrt{T_{1} \cdot T_{2}}} \\\\ R e=-k \frac{T_{1} \cdot T_{2}}{T_{1}+T_{2}} \\\\ \text { 渐近线: }-k\left(T_{1}+T_{2}\right)【可以不求】 \end{array}
G(s)=s(T1?s+1)(T2?s+1)k?与实轴交点处:ωx?=T1??T2??1?Re=?kT1?+T2?T1??T2???渐近线:??k(T1?+T2?)【可以不求】?
图像【图中黑色线】
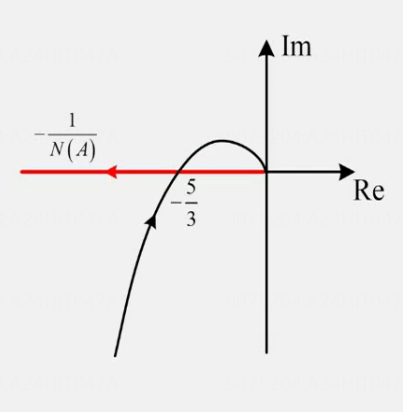
解题思路
1. 非线性的合并化简
通过特征方程法【就是第一张学过的那个回路相加】,或者等效结构图法【同样是第一章学过的结构图化简,化简成一个反馈回路且回路中只有非线性部分+线性部分即可】
注意:这两种等效有时候都会改变输出!
极个别题目问输出的一些性质,此时最好用结构图法【特征方程法】
比如: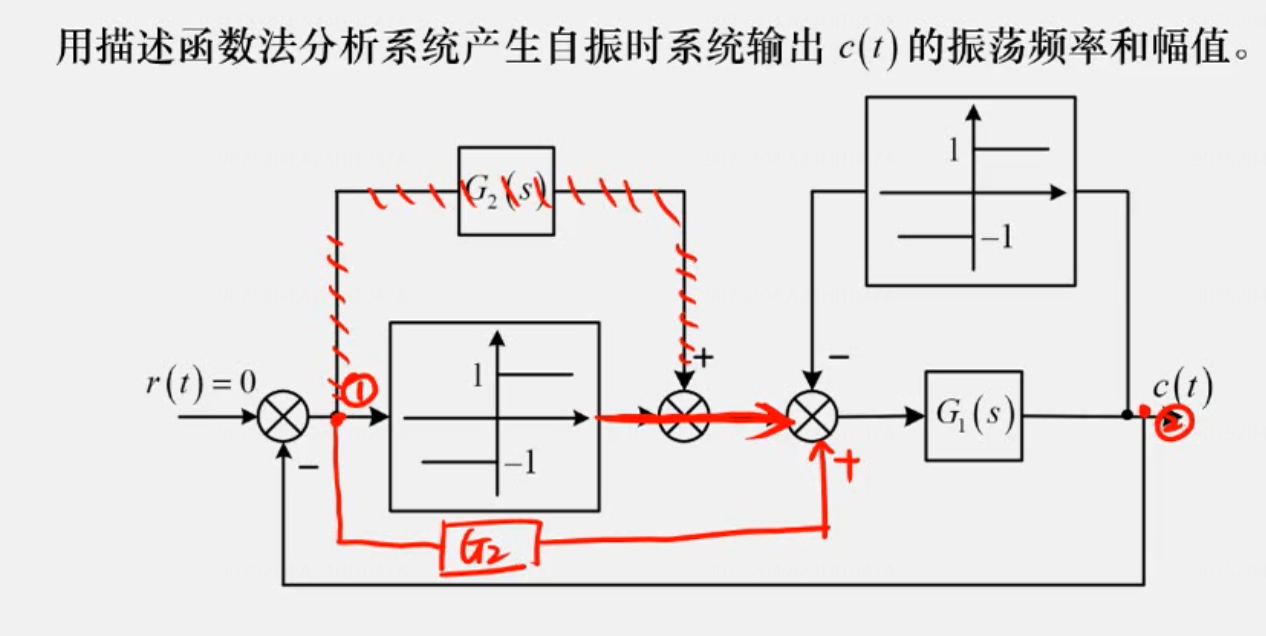
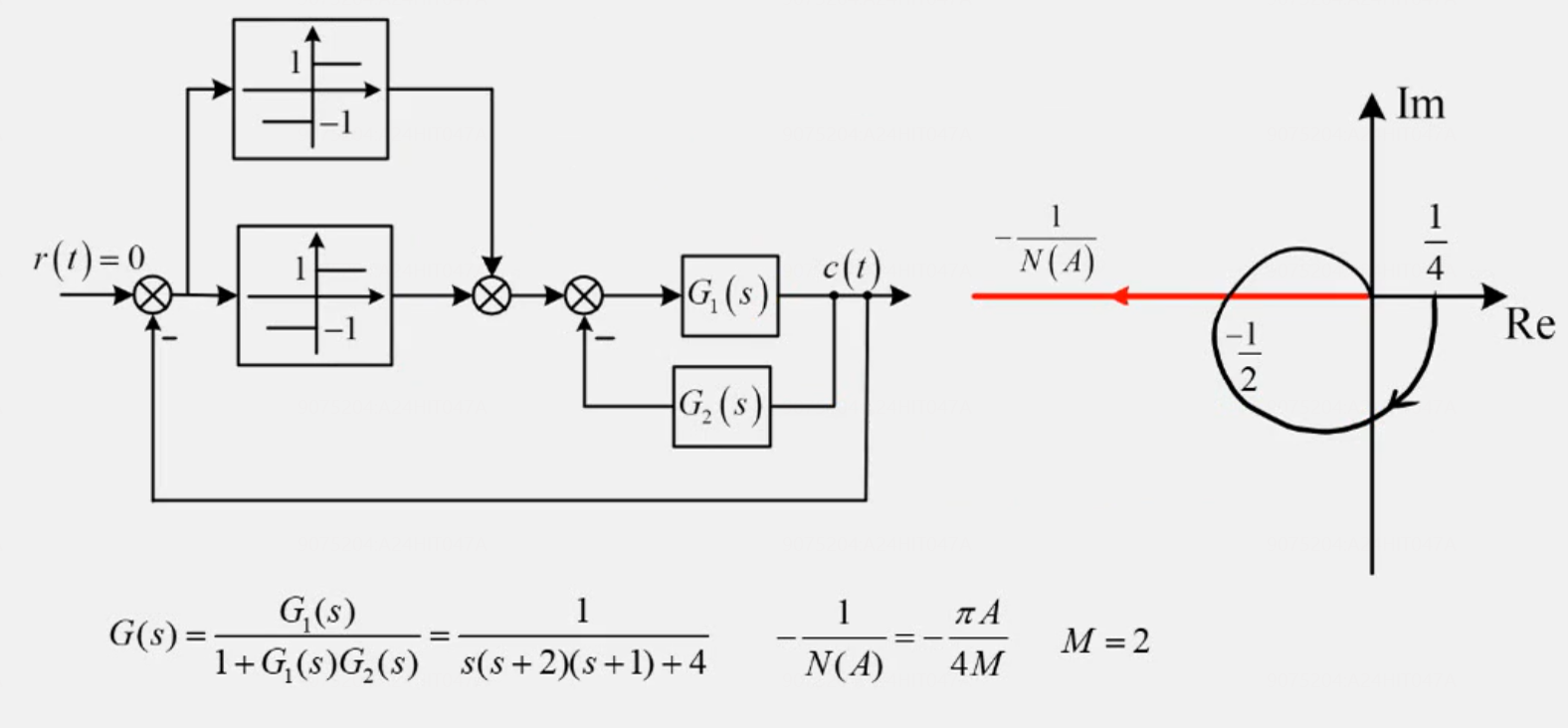
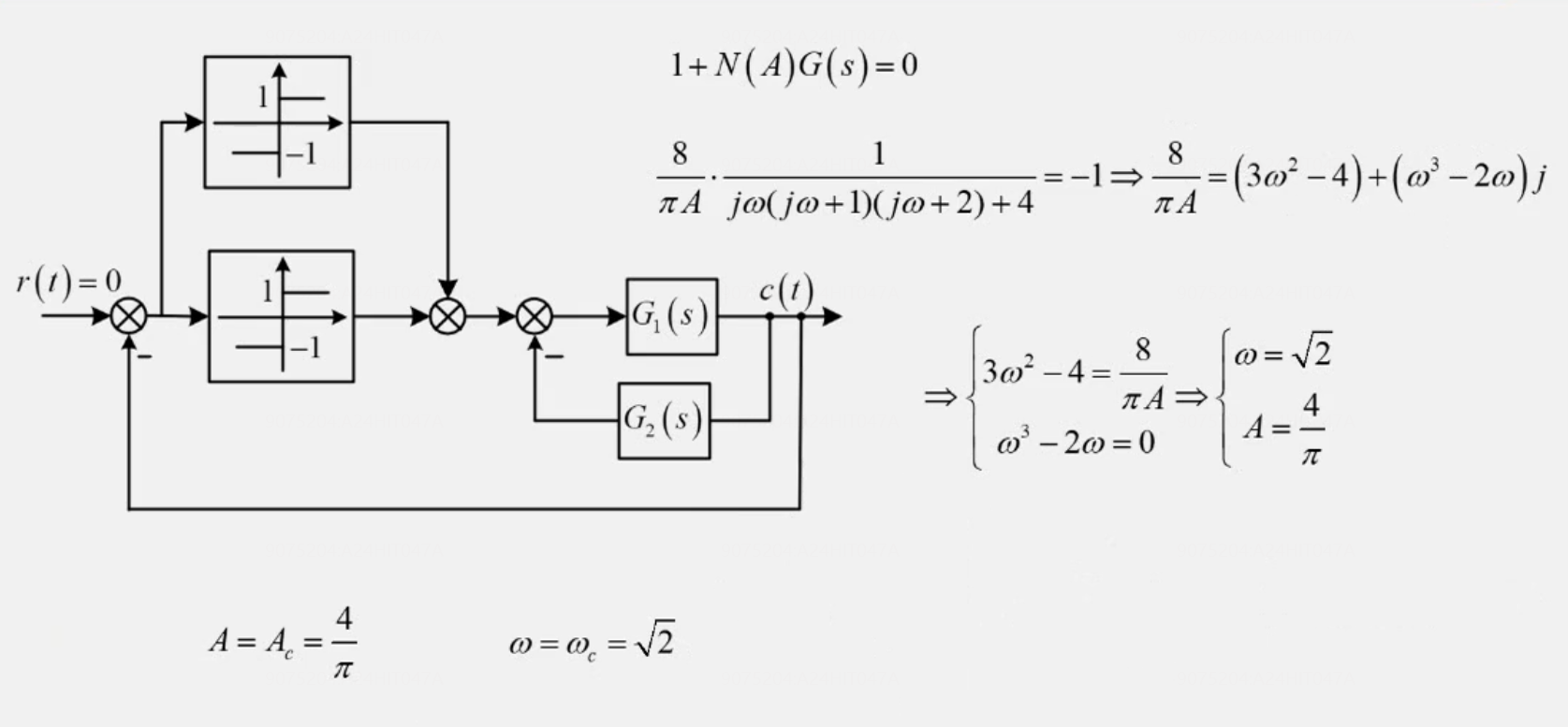
2 考察公式背诵,广义(-1,j0)点相关性质
求出真正的极限环【从不稳定走向稳定】的点和频率特征
利用线性部分与实轴交点、广义(-1,j0)点的一些性质解题
李雅普诺夫
基础知识
状态稳定(内部稳定)vs输出稳定(BIBO稳定、外部稳定)【仅针对定常系统】
在之前的传统控制中,我们要求的是输出稳定,即BIBO稳定,只需要极点具有负实部,这是输出稳定
现在在多输入多输出中,我们引入了状态变量。稳定性只取决于系统的结构和参数,和系统的初始条件及扰动、输出等无关。因此只需考虑A矩阵;状态稳定指A矩阵所有特征值小于零,这是状态稳定
状态稳定可以推输出稳定【
y
=
C
x
y=Cx
y=Cx,状态乘以系数就得到输出了,因此稳定性不会变化】
但是输出稳定不能推状态稳定

平衡状态与平衡点
状态指的是高阶导数恒等于零的状态(?)
点指的就是那个点

补充
线性定常系统只有一个平衡状态
李雅普诺夫意义下的稳定性定义:“小圆内的点离不开大圆”
“小圆内的点离不开大圆”

直观解释

渐近稳定:“小圆内的点趋向于零点”
如果平衡点不在零点,可以通过平移手段将平衡点变为零点,因此统一以零点为考量
直观解释
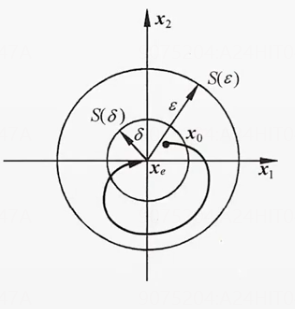
大范围渐近稳定:“任何点趋向于零点”
直观解释【同上图】

二次型标量函数:即实矩阵对应的二次型形式

希尔维斯特判据:判断矩阵的正负定情况

补充说明?【包括一个比较重要的线性定常系统结论】
- 稳定与一致稳定在线性定常系统中等价
- 等幅振荡是李雅普诺夫意义下的稳定
- 线性定常系统只有一个平衡状态
- 线性定常系统如果渐近稳定,则一定大范围渐近稳定
- 李雅普诺夫意义下的稳定包含渐近稳定
【临界稳定+渐近稳定=李雅普诺夫意义下稳定】
李一(间接法)
线性系统 判断渐近稳定/李雅普诺夫意义下稳定的方法

非线性系统? 判断稳定性【不存在矩阵A了】
处理方法:线性化处理
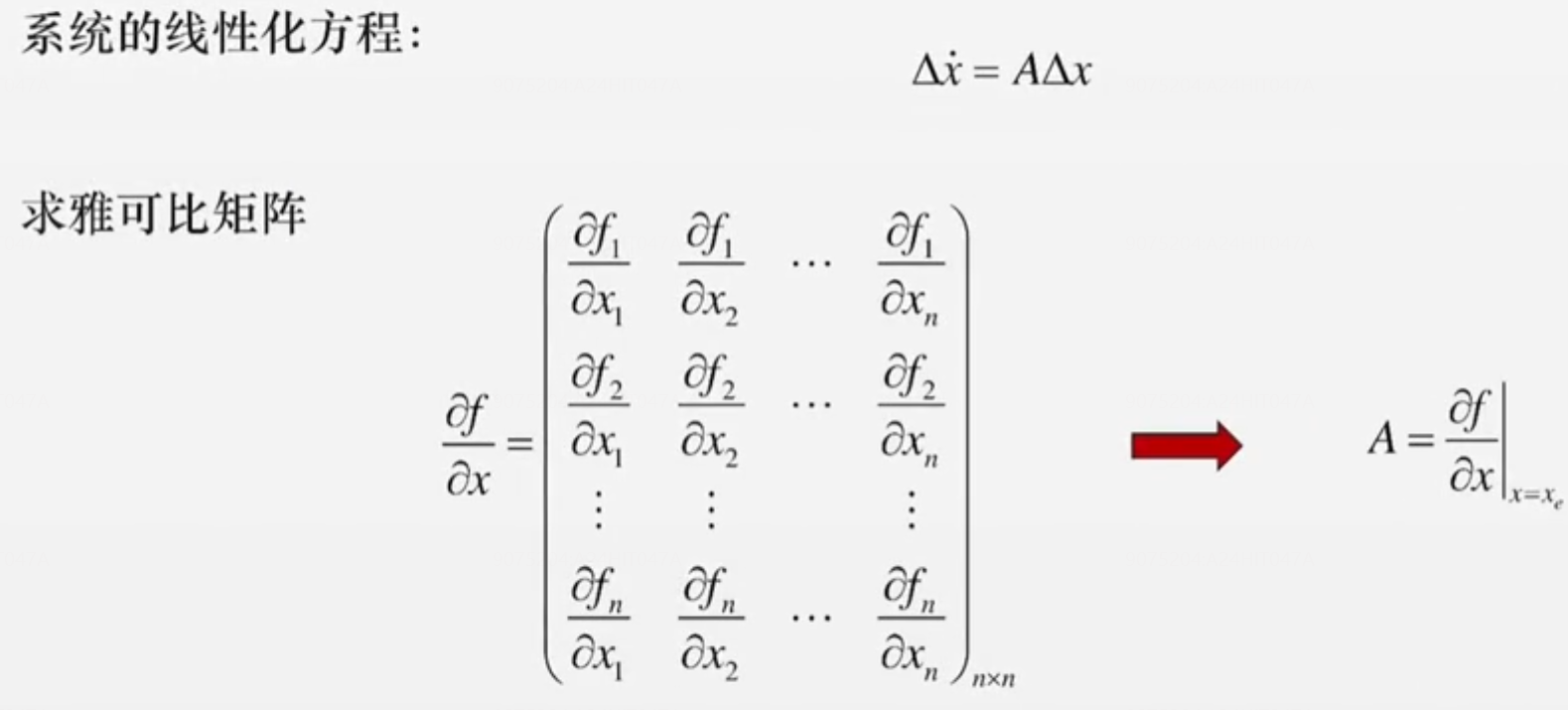
渐近稳定的充要条件是所有特征值具有负实部,如果有实部为零的根,方法失效
举例1 非线性系统判断稳定性例题

李二(直接法)
基本思路
借助李雅普诺夫函数 V ( x ) V(x) V(x)直接判断系统稳定性,是从能量的观点进行分析的
求解方法1 选取标量函数

从能量的角度考虑
V
˙
(
x
)
\dot V(x)
V˙(x)正定说明能量一直增大,就“飞走了”
V
˙
(
x
)
\dot V(x)
V˙(x)负定说明能量一直减小,就“收敛了”
有求解方法可知,李雅普诺夫意义下的稳定包含渐近稳定
补充 V ˙ ( x ) ≡ 0 \dot V(x)\equiv 0 V˙(x)≡0也是半负定,李雅普诺夫意义下稳定
举例1🌟 稍微复杂一点的渐近稳定判据

在这道题
V
˙
(
x
)
\dot V(x)
V˙(x)判断出半负定之后,应该判断有没有可能
V
˙
(
x
)
≡
0
\dot V(x)\equiv 0
V˙(x)≡0【即求出系统的所有受扰运动解】,判断方法如下:
在条件
V
˙
(
x
)
≡
0
\dot V(x)\equiv 0
V˙(x)≡0下,有
x
2
=
0
x_2 = 0
x2?=0 则
x
˙
2
≡
0
\dot x_2 \equiv 0
x˙2?≡0
根据状态方程,可知
x
1
=
0
x_1=0
x1?=0,从而只在平衡点满足要求
注意书写过程!
求解方法2 李二在线性系统中的应用🌟
一些推导过程
设线性定常连续系统中有
x ˙ = A x \dot x = A x x˙=Ax
取李雅普诺夫函数为二次型标量函数:
V ( x ) = x T P x V(x)=x^{T} P x V(x)=xTPx
则:
V ˙ ( x ) = x T P x ˙ + x ˙ T P x = x T P A x + ( A x ) T P x = x T ( P A + A T P ) x = ? x T Q x \dot{V}(x)=x^{T} P \dot{x}+\dot{x}^{T} P x=x^{T} P A x+(A x)^{T} P x\\=x^{T}\left(P A+A^{T} P\right) x=-x^{T} Q x V˙(x)=xTPx˙+x˙TPx=xTPAx+(Ax)TPx=xT(PA+ATP)x=?xTQx
其中Q满足:
A T P + P A = ? Q A^{T} P+P A=-Q ATP+PA=?Q
李雅普诺夫方程为【P、Q均为对称阵】
A
T
P
+
P
A
=
?
Q
A^{T} P+P A=-Q
ATP+PA=?Q
如果满足P正定、Q正定,则平衡状态就是渐近稳定的
补充说明
- 线性定常该系统的平衡状态在零点
- 🌟🌟实际应用时,通常先取一个正定矩阵 Q Q Q,常取 Q = I Q=I Q=I,然后带入李雅普诺夫方程,判定 P P P的正定性。
- 若 V ˙ ( x ) \dot V(x) V˙(x)不恒为零,那么 Q Q Q可取为半正定的。【一般也用不到】
- 按照这种方法,也可以把 V ( x ) V(x) V(x)和 V ˙ ( x ) \dot V(x) V˙(x)写出来,利用李一验证 V ˙ ( x ) \dot V(x) V˙(x)【考试不用写】
举例1 李二经典题,令Q为单位阵,求P

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 从Scroll怒喷社区用户事件,看L2龙头ZKFair的做事格局
- Dash+Plotly | Web应用开发(1)
- AI经典科幻电影《第六日2:觉醒》(上)
- python语言在web上的应用:如何节省服务器资源?
- JavaWeb——第六章 会话_过滤器_监听器
- 学习python第八天
- SpringSecurity 密码加密登录
- 文件销毁 硬盘销毁 数据销毁:护航数据安全的最后一公里
- vue 导出时身份证E+16,如何改邪归正
- 电脑/设备网络共享给其他设备上网

